Målinger af position, central tendens og spredning

Det målinger af central tendens, spredning og position, er værdier, der bruges til korrekt fortolkning af et sæt statistiske data. Disse kan bearbejdes direkte, da de fås fra den statistiske undersøgelse, eller de kan organiseres i grupper med lige frekvens, hvilket letter analysen..

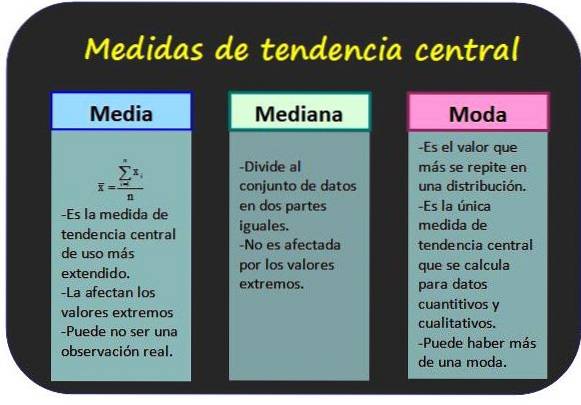
Foranstaltninger af central tendens

De giver mulighed for at vide, hvilke værdier de statistiske data er grupperet.

Aritmetisk gennemsnit

Det er også kendt som gennemsnittet af værdierne for en variabel og opnås ved at tilføje alle værdierne og dividere resultatet med det samlede antal data.

• Aritmetisk gennemsnit for ikke-grupperede data

Lad være en variabel x, som vi har n data uden at organisere eller gruppere, dens aritmetiske gennemsnit beregnes som følger:

Og sammenfattende notation:

Eksempel

Ejerne af en bjergturistkrog har til hensigt at vide, hvor mange dage de besøgende i gennemsnit forbliver i faciliteterne. Til dette blev der ført en oversigt over de dage, hvor 20 grupper af turister varede, og opnåede følgende data:

1; 1; to; to; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; to; to; 3; 4; 1

Det gennemsnitlige antal dage, som turister overnatter, er:

• Aritmetisk gennemsnit for grupperede data

Hvis dataene for variablen er organiseret i en tabel over absolutte frekvenser f_jeg og klassecentrene er x₁, x_to,..., x_n, middelværdien beregnes ved:

Sammenfattende notation:

Median

Medianen for en gruppe af n-værdier for variablen x er gruppens centrale værdi, forudsat at værdierne er ordnet i stigende rækkefølge. På denne måde er halvdelen af ​​alle værdier mindre end tilstanden, og den anden halvdel er større..

• Median af ikke-grupperede data

Følgende tilfælde kan forekomme:

-Antal n af værdierne for variablen x  ulige: medianen er den værdi, der er lige midt i gruppen af ​​værdier:

-Antal n af værdierne for variablen x par: i dette tilfælde beregnes medianen som gennemsnittet af de to centrale værdier i datagruppen:

Eksempel

For at finde medianen for dataene fra turisthostellet bestilles de først fra laveste til højeste:

1; 1; 1; 1; 1; 1; 1; to; to; to; to; 3; 3; 3; 4; 4; 4; 4; 5; 5

Antallet af data er lige, derfor er der to centrale data: X₁₀ og X_elleve og da begge er værd 2, er deres gennemsnit også.

Median = 2

• Median af samlede data

Følgende formel anvendes:

Symbolerne i formlen betyder:

-c: bredde på intervallet, der indeholder medianen

-B_M: nedre grænse for det samme interval

-F_m: antal observationer indeholdt i det interval, som medianen hører til.

-n: samlede data.

-F_BM: antal observationer Før af intervallet, der indeholder medianen.

mode

Tilstanden for ikke-grupperede data er den værdi med den højeste frekvens, mens den for grupperede data er den klasse med den højeste frekvens. Mode betragtes som den mest repræsentative data eller klasse for distributionen.

To vigtige egenskaber ved denne foranstaltning er, at et datasæt kan have mere end en tilstand, og tilstanden kan bestemmes for både kvantitative og kvalitative data..

Eksempel

Fortsat med dataene fra turistparadoren er den, der gentages mest, 1, derfor er den mest almindelige ting, at turister bliver 1 dag i paradoren.

Målinger af spredning

Målinger af spredning beskriver, hvor klyngede data er omkring de centrale mål.

Rang

Det beregnes ved at trække de største data og de mindste data. Hvis denne forskel er stor, er det et tegn på, at dataene er spredt, mens små værdier indikerer, at dataene er tæt på gennemsnittet..

Eksempel

Området for data fra turistparador er:

Område = 5−1 = 4

Variation

• Variant for ikke-grupperede data

For at finde variansen s^to Det er nødvendigt først at kende det aritmetiske gennemsnit, derefter den kvadratiske forskel mellem hvert stykke data og gennemsnittet beregnes, alle tilføjes og divideres med det samlede antal observationer. Disse forskelle er kendt som afvigelser.

Variansen, som altid er positiv (eller nul), angiver, hvor langt observationerne er fra gennemsnittet: hvis variansen er høj, er værdierne mere spredte, end når variansen er lille.

Eksempel

Variationen for data fra turisthostel er:

1; 1; to; to; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; to; to; 3; 4; 1

• Variant for grupperede data

For at finde variansen af ​​et grupperet datasæt kræves følgende: i) middelværdien, ii) frekvensen f_jeg  som er de samlede data i hver klasse og iii) x_jeg  eller klasse værdi:

Standardafvigelsen er den positive kvadratrod af variansen, så den har en fordel i forhold til variansen: den kommer i de samme enheder som variablen, der undersøges, og du har således en mere direkte idé om, hvor tæt eller langt variablen er fra gennemsnittet.

• Standardafvigelse for ikke-grupperede data

Det bestemmes simpelthen ved at finde kvadratroden af ​​variansen for ikke-grupperede data:

Standardafvigelsen for data fra turisthostel er:

s = √ (s^to) = √1.95 = 1.40

• Standardafvigelse for grupperede data

Det beregnes ved at finde kvadratroden af ​​variansen for grupperede data:

Positionsmålinger

Måling af position opdeler et ordnet datasæt i stykker af samme størrelse. Medianen, ud over at være et mål for central tendens, er også et mål for position, da den deler helheden i to lige store dele. Men mindre dele kan opnås med kvartiler, deciler og percentiler.

Kvartiler

Kvartilerne opdeler sættet i fire lige store dele, der hver indeholder 25% af dataene. De betegnes som Q₁, Spørgsmål_to og Q₃ og medianen er kvartilen Q_to. På denne måde er 25% af dataene under Q-kvartilen.₁, 50% under Q-kvartilen_to eller median og 75% under Q-kvartilen₃.

• Kvartiler til ikke-grupperede data

Dataene bestilles, og summen er opdelt i 4 grupper med det samme antal data hver. Positionen for det første kvartil findes af:

Spørgsmål₁ = (n + 1) / 4

Hvor n er de samlede data. Hvis resultatet er et heltal, lokaliseres de data, der svarer til denne position, men hvis det er decimal, beregnes dataene svarende til heltalets gennemsnit med det næste, eller for større præcision interpoleres det lineært mellem dataene.

Eksempel

Positionen for det første kvartil Q₁ for data fra turist parador er:

Spørgsmål₁ = (n + 1) / 4 = (20 + 1) / 4 = 5,25

Dette er positionen for kvartil 1, og da resultatet er decimal, søges data X₅ og X_6, som henholdsvis er X₅ = 1 og X₆ = 1 og er gennemsnit, hvilket resulterer i:

Første kvartil = 1

1; 1; 1; 1; 1; 1; 1; to; to; to; to; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Positionen for det andet kvartil Q_to det er:

Spørgsmål_to = 2 (n + 1) / 4 = 10,5

Hvad er gennemsnittet mellem X₁₀ og X_elleve og matcher medianen:

Andet kvartil = Median = 2

Placeringen af ​​det tredje kvartil beregnes af:

Spørgsmål₃ = 3 (n + 1) / 4 = 3 (20 + 1) / 4 = 15,75

Det er også decimal, og derfor beregnes X i gennemsnit_femten og X₁₆:

1; 1; 1; 1; 1; 1; 1; to; to; to; to; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Men da begge er værd 4:

Tredje kvartil = 4

Den generelle formel for placering af kvartiler i ikke-grupperede data er:

Spørgsmål_k = k (n + 1) / 4

Med k = 1,2,3.

• Kvartiler til grupperede data

De beregnes på samme måde som medianen:

Forklaringen på symbolerne er:

-B_Spørgsmål: nedre grænse for intervallet, der indeholder kvartilen

-c: bredden af ​​dette interval

-F_hvad: antal observationer indeholdt i kvartilintervallet.

-n: samlede data.

-F_BQ: antal data Før af intervallet, der indeholder kvartilen.

Deciler og percentiler

Deciler og percentiler opdeler datasættet i henholdsvis 10 lige store dele og 100 lige store dele, og deres beregning udføres på samme måde som kvartilernes.

• Deciler og percentiler til ikke-grupperede data

Formlerne anvendes henholdsvis:

D_k = k (n + 1) / 10

Med k = 1,2,3… 9.

Decile D₅ skal være lig medianen.

P_k = k (n + 1) / 100

Med k = 1,2,3… 99.

P-percentilen_halvtreds skal være lig medianen.

Eksempel

I eksemplet med turisthostel, D's position₃ det er:

D₃ = 3 (20 + 1) / 10 = 6,3

Da det er et decimaltal, beregnes X i gennemsnit₆ og X_7, begge er lig med 1:

1; 1; 1; 1; 1; 1; 1; to; to; to; to; 3; 3; 3; 4; 4; 4; 4; 5; 5

Det betyder, at 3 tiendedele af dataene er under X₇ = 1 og de resterende ovenfor.

• Deciler og percentiler til grupperede data

Formlerne er analoge med dem for kvartiler. D bruges til at betegne deciler og P for percentiler, og symbolerne fortolkes ens:

Den empiriske regel

Når dataene er symmetrisk fordelt, og fordelingen er unimodal, kaldes der en regel  empirisk regel eller regel 68 - 95 - 99, der grupperer dem i følgende intervaller:

• 68% af dataene er inden for området:

• 95% af dataene er i området:

• 99% af dataene er inden for området:

Eksempel

I hvilket interval er 95% af dataene fra turistparadoren?

De er i intervallet: [2.5−1.40; 2,5 + 1,40] = [1,1; 3.9].

Referencer

1. Berenson, M. 1985. Statistik for ledelse og økonomi. Interamericana S.A.
2. Devore, J. 2012. Sandsynlighed og statistik for ingeniørvidenskab og videnskab. 8. plads Udgave. Cengage.
3. Levin, R. 1988. Statistik for administratorer. 2. plads Udgave. Prentice hall.
4. Spiegel, M. 2009. Statistik. Schaum-serien. 4. plads Udgave. Mcgraw bakke.
5. Walpole, R. 2007. Sandsynlighed og statistik for ingeniørvidenskab og videnskab. Pearson.