
Inertimomentformler, ligninger og beregningseksempler

Det inertimoment af et stift legeme i forhold til en bestemt rotationsakse, repræsenterer dets modstand mod at ændre sin vinkelhastighed omkring nævnte akse. Det er proportionalt med massen og også til placeringen af rotationsaksen, da kroppen ifølge sin geometri lettere kan rotere omkring bestemte akser end i andre.
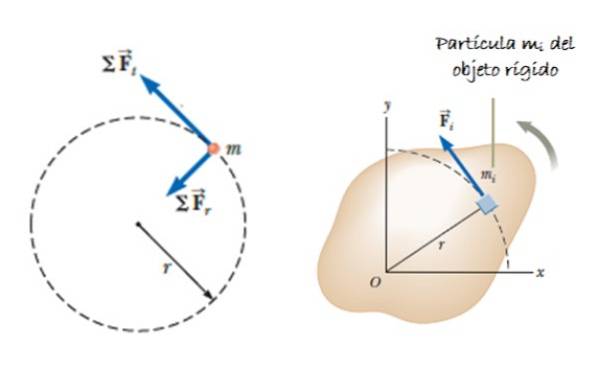
Antag et stort objekt (bestående af mange partikler), som kan rotere omkring en akse. Antag at en styrke virker F, anvendt tangentielt på masseelementet Δmjeg, der producerer et drejningsmoment eller øjeblik, givet af τnet = ∑rjeg x Fjeg. Vektoren rjeg er positionen for Δmjeg (se figur 2).

Dette øjeblik er vinkelret på rotationsplanet (retning +k = kommer ud af papiret). Da kraften og den radiale positionsvektor altid er vinkelret, forbliver krydsproduktet:
τnet = ∑ Fjeg rjeg k = ∑ (Δmjeg tiljeg) rjeg k = ∑ Δmjeg (tiljeg rjeg ) k
Acceleration tiljeg repræsenterer den tangentielle komponent af acceleration, da radial acceleration ikke bidrager til drejningsmoment. Som en funktion af vinkelacceleration α kan vi indikere, at:
tiljeg = α rjeg
Derfor ser nettomomentet sådan ud:
τnet = ∑ Δmjeg (α rjegto) k = (∑ rjegto Δmjeg) a k
Vinkelaccelerationen α er den samme for hele objektet, derfor påvirkes den ikke af abonnementet "i" og kan forlade summeringen, hvilket er netop det øjebliks inerti, der symboliseres med bogstavet I:
I = ∑ rjegto Δmjeg
Dette er inertimomentet for en diskret massefordeling. Når fordelingen er kontinuerlig, erstattes summeringen med en integral og Δm bliver en massedifferentiale dm. Integralet udføres over hele objektet:
Jeg = ∫M(rto) dm
Enhederne af inertimomentet i SI International System er kg x mto. Det er en skalær og positiv størrelse, da det er produktet af en masse og en kvadrat af en afstand.
Artikelindeks
- 1 Eksempler på beregning
- 1.1 Trægningsmoment for en tynd stang i forhold til en akse, der passerer gennem dens centrum
- 1.2 Træghedsmoment for en disk i forhold til en akse, der passerer gennem dens centrum
- 1.3 Trægningsmoment for en fast kugle i forhold til en diameter
- 1.4 Træghedsmoment for en solid cylinder i forhold til den aksiale akse
- 1.5 Trækmoment for et rektangulært ark i forhold til en akse, der passerer gennem dets centrum
- 1.6 Trækmoment for et firkantet ark i forhold til en akse, der passerer gennem dets centrum
- 2 Inerti-sætninger
- 2.1 Steiners sætning
- 2.2 Vinkelret aksesætning
- 3 Øvelse løst
- 4 Referencer
Beregningseksempler
Et udvidet objekt, såsom en bar, disk, sfære eller andet, hvis densitet ρ er konstant og at vide, at densiteten er massevolumenforholdet, massedifferentialet dm er skrevet som:
ρ = dm / dV → dm = ρdV
Ved at erstatte integralet for inertimomentet har vi:
I = ∫rto ρdV = ρ ∫rtodV
Dette er et generelt udtryk, gyldigt for et tredimensionelt objekt, hvis volumen V og position r er funktioner i de geografiske koordinater x, Y Y z. Bemærk at densitet er konstant uden for integralet.
Tætheden ρ Det er også kendt som volumetrisk tæthed, men hvis objektet er meget fladt, som et ark eller meget tyndt og smalt som en stang, kan andre former for tæthed bruges, lad os se:
- For et meget tyndt ark er densiteten, der skal bruges σ, overfladetætheden (masse pr. Arealeenhed) og giver er arealdifferentialet.
- Og hvis det er en tynd stang, hvor kun længden er relevant, anvendes den lineære massefylde λ og en længdeforskel i henhold til den akse, der anvendes som reference.
I de følgende eksempler betragtes alle objekter som stive (ikke deformerbare) og har ensartet tæthed.
Trægemoment for en tynd stang i forhold til en akse, der passerer gennem dens centrum
Her skal vi beregne inertimomentet for en tynd, stiv, homogen stang med længde L og masse M i forhold til en akse, der passerer gennem midten.
For det første er det nødvendigt at etablere et koordinatsystem og opbygge en figur med den passende geometri, sådan:
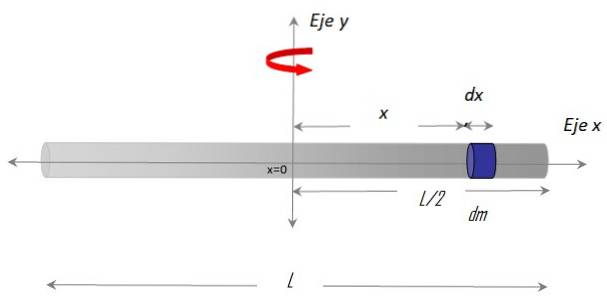
Det X-akse langs baren og Akse y som rotationsaksen. Proceduren for at etablere integralet kræver også at vælge en massedifferentiale over bjælken, kaldet dm, som har en differentiel længde dx og er placeret på positionen x vilkårlig i forhold til centrum x = 0.
Ifølge definitionen af lineær massefylde λ:
λ = M / L
Da densiteten er ensartet, hvilket er gyldig for M og L, er den også gyldig for dm og dx:
λ = dm / dx → dm = λdx.
På den anden side er masseelementet i position x, så ved at erstatte denne geometri i definitionen har vi en bestemt integral, hvis grænser er enderne af bjælken i henhold til koordinatsystemet:
Erstatning af den lineære densitet λ = M / L:

For at finde stregens inertimoment i forhold til en anden rotationsakse, for eksempel en, der passerer gennem en af dens yderpunkter, kan du bruge Steiners sætning (se øvelse løst i slutningen) eller udføre en direkte beregning svarende til den vist her, men ændrer geometrien korrekt.
Træghedsmoment for en disk i forhold til en akse, der passerer gennem dens centrum
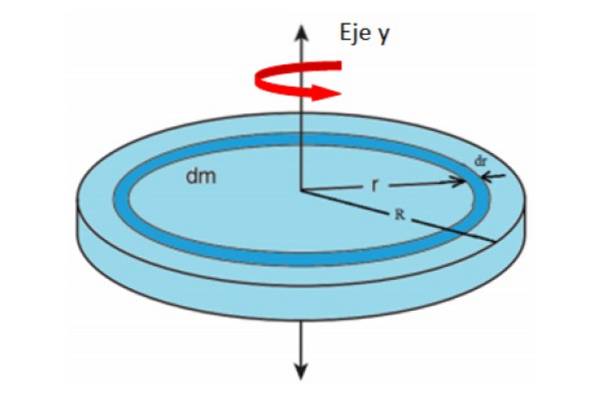
En meget tynd skive med ubetydelig tykkelse er en flad figur. Hvis massen fordeles ensartet over hele overfladen af område A, er massefylden σ:
σ = M / Y
Så meget dm Hvad giver svarer til massen og arealet af differentieringen vist i figuren. Vi antager, at hele samlingen roterer omkring y-aksen.
Du kan forestille dig, at disken er sammensat af mange koncentriske ringe med radius r, hver med sit respektive inertimoment. Tilføjelse af bidragene fra alle ringene, indtil de når radius R, diskens samlede inertimoment vil være.
σ = dm / dA → dm = σgiver

Hvor M repræsenterer hele disken. Arealet på en disk afhænger af dens radius r som:
A = π.rto
Udledning med hensyn til r:
dA / dr = 2 = 2π.r → dA = 2π.rdr
Udskiftning af ovenstående i definitionen af I:

Erstatning af σ = M / (π.Rto ) forbliver:
%5Cleft&space;(%5Cfrac%7BR%5E%7B4%7D%7D%7B4%7D&space;%5Cright&space;)=%5Cfrac%7B1%7D%7B2%7DMR%5E%7B2%7D)
Træghedsmoment for en fast kugle i forhold til en diameter
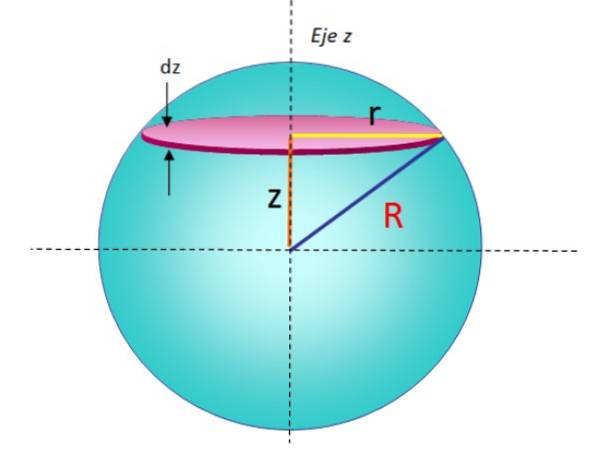
En sfære med radius R kan betragtes som en række diske stablet oven på den anden, hvor hver disk med uendelig masse dm, radio r og tykkelse dz, har et inerti-øjeblik givet af:
gavdisk = (½) rtodm
For at finde denne forskel tog vi simpelthen formlen fra det foregående afsnit og erstattede M Y R til dm Y r, henholdsvis. En disk som denne kan ses i geometrien i figur 5.

Ved at tilføje alle de uendelige minimale øjeblikke af inerti af stablede diske opnås det samlede inertimoment af kuglen:
jegkugle = ∫dIdisk
Hvilket svarer til:
Jeg = ∫kugle (½) rtodm
For at løse integralet skal du udtrykke dm korrekt. Som altid opnås det ud fra densiteten:
ρ = M / V = dm / dV → dm = ρ.dV
Lydstyrken på en differentiel disk er:
dV = Areal af base x højde
Diskens højde er tykkelsen dz, mens bundområdet er πrto, Dermed:
dV = πrtodz
Og ved at erstatte den foreslåede integral vil det se sådan ud:
Jeg = ∫kugle(½) rtodm = ∫ (½) rto(ρπrtodz)
Men inden integrering skal det bemærkes, at r-diskens radius afhænger af z og R-sfæreens radius, som det fremgår af figur 5. Brug af Pythagoras sætning:
Rto = rto + zto → rto = Rto - zto
Hvilket fører os til:
Jeg = ∫kugle(½) ρ rto(πrtodz) = ∫kugle(½) ρ π r4dz= ∫kugle(½) ρ π (Rto - zto)to dz
For at integrere over hele sfæren bemærker vi, at z varierer mellem -R og R, derfor:

At vide det ρ = M / V = M / [(4/3) πR3] endelig opnås det efter forenkling:

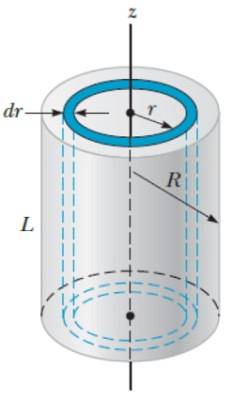
Trægningsmoment for en solid cylinder i forhold til den aksiale akse
Til dette objekt anvendes en metode svarende til den, der anvendes til sfæren, kun denne gang er det lettere, hvis cylinderen forestilles at være dannet af cylindriske skaller med radius r, tykkelse dr og højde H, som om de var lagene af en løg.

Lydstyrken dV af et cylindrisk lag er:
dV = 2π.rL.dr
Derfor er skalmassen:
dm = ρ.dV = ρ. 2π.r.L.dr
Dette udtryk er substitueret i definitionen af inertimoment:

Ovenstående ligning indikerer, at cylinderens inertimoment ikke afhænger af længden, men kun af dens masse og radius. Ja L ændret, ville inertimomentet omkring den aksiale akse forblive det samme. Af denne grund, jeg af cylinderen falder sammen med den for den tidligere beregnede tynde skive.
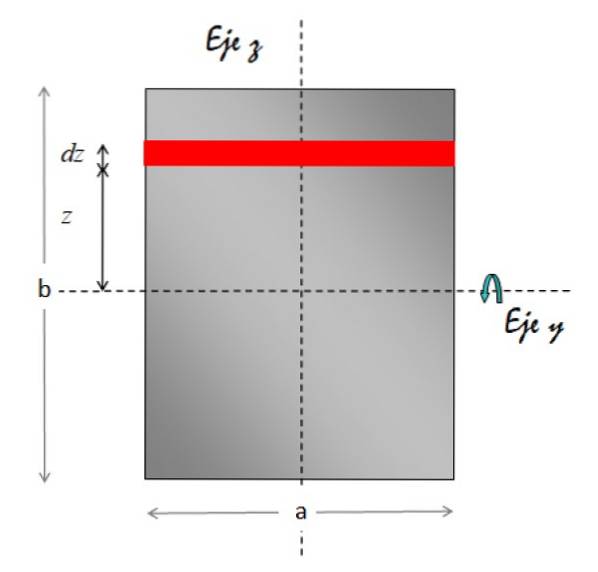
Trækmoment for et rektangulært ark i forhold til en akse, der passerer gennem dets centrum
Det Akse y vandret rotationsakse. Figuren nedenfor viser den geometri, der kræves for at udføre integrationen:

Områdeelementet markeret med rødt er rektangulært. Dets areal er base x højde, derfor:
dA = a.dz
Derfor er massedifferentialet:
dm = σ.dA = σ. (a.dz)
Med hensyn til afstanden fra arealelementet til rotationsaksen er det altid z. Vi erstatter alt dette i integriteten af inertimomentet:
Nu erstattes overflademassefylden σ med:
σ = M / ab
Og det ser bestemt sådan ud:

Bemærk, at det er som det med den tynde stang.
Trækmoment for et firkantet ark i forhold til en akse, der passerer gennem dets centrum
For et sidefyrkant L, i det foregående udtryk gyldigt for et rektangel skal du blot erstatte værdien af b til den af L:

Moment af inerti sætninger
Der er to sætninger, der er særligt nyttige til at forenkle beregningen af inertimomenter omkring andre akser, som ellers kunne være vanskelige at finde på grund af manglende symmetri. Disse sætninger er:
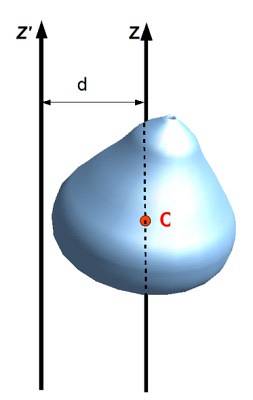
Steiners sætning
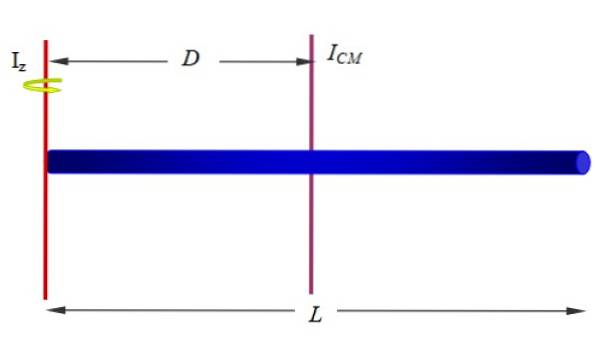
Også kaldet sætning med parallelle akser, vedrører inertimomentet med hensyn til en akse med en anden, der passerer gennem massens centrum af objektet, så længe akserne er parallelle. For at anvende det er det nødvendigt at kende afstanden D mellem begge akser og naturligvis objektets masse M.
Være jegz inertimomentet for et udvidet objekt med hensyn til z-aksen, ICM inertimomentet i forhold til en akse, der passerer gennem massecentret (CM) af objektet, så er det rigtigt, at:
jegz = JegCM + MDto
Eller i notationen af følgende figur: jegz ' = Jegz + Mdto

Vinkelret aksesætning
Denne sætning anvendes på plane overflader og går således: inertimomentet for et plant objekt omkring en akse vinkelret på det er summen af inertimomenterne omkring to akser vinkelret på den første akse:
jegz = Jegx + jegY
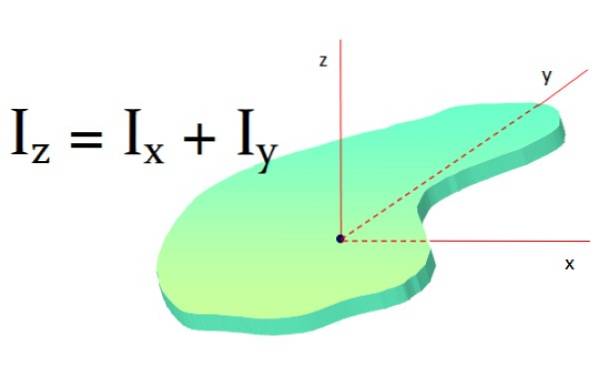
Hvis objektet har en sådan symmetri jegx og jegY er lige, så er det rigtigt, at:
jegz = 2Ix
Træning løst
Find stregens inertimoment i forhold til en akse, der passerer gennem en af dens ender, som vist i figur 1 (nedenfor og til højre) og figur 10.
Opløsning:
Vi har allerede inertimomentet for bjælken omkring en akse, der passerer gennem dens geometriske centrum. Da stangen er homogen, er dens massepunkt på det tidspunkt, så dette vil være vores jegCM at anvende Steiners sætning.
Hvis stangens længde er L, z-aksen er i en afstand D = L / 2, derfor:
jegz = JegCM + MDto= (1/12) MLto+M (L / 2)to= (1/3) MLto
Referencer
- Bauer, W. 2011. Fysik til ingeniørvidenskab. Bind 1. Mc Graw Hill. 313-340
- Rex, A. 2011. Grundlæggende fysik. Pearson. 190-200.
- Parallel akse sætning. Gendannet fra: hyperphysics.phy-astr.gsu.edu.
- Serway, R. 2018. Fysik til videnskab og teknik. Bind 1. Cengage.
- Sevilla Universitet. Inertimoment af sfæriske faste stoffer. Gendannet fra: laplace.us.es.
- Sevilla Universitet. Inertimoment for et partikelsystem. Gendannet fra: laplace.us.es.
- Wikipedia. Parallelakse sætning. Gendannet fra: en.wikipedia.org



Endnu ingen kommentarer