
Momentkarakteristika og formler, øvelser

Det drejningsmoment, moment eller moment af en kraft er en styrkes evne til at forårsage en drejning. Etymologisk modtager det drejningsmomentets navn som en afledning af det engelske ord drejningsmoment, fra latin torquere (vride).
Momentet (i forhold til et givet punkt) er den fysiske størrelse, der er resultatet af fremstilling af vektorproduktet mellem positionsvektorerne for det punkt, hvor kraften påføres, og den for den udøvede kraft (i den angivne rækkefølge). Dette øjeblik afhænger af tre hovedelementer.
Det første af disse elementer er størrelsen af den påførte kraft, det andet er afstanden mellem det punkt, hvor det påføres, og det punkt, i forhold til hvilket kroppen roterer (også kaldet løftearmen), og det tredje element er vinklen af anvendelsen af nævnte kraft.
Jo større kraft, jo større spin. Det samme sker med løftearmen: jo større afstanden er mellem det punkt, hvor kraften påføres, og det punkt, som det drejer sig om, jo større vil dette være.
Selvfølgelig er momentet af særlig interesse i byggeri og industri, såvel som det er til stede i utallige anvendelser til hjemmet, som når en møtrik strammes med en skruenøgle..
Artikelindeks
- 1 Formler
- 1.1 Enheder
- 2 funktioner
- 3 Resulterende drejningsmoment
- 4 applikationer
- 5 Øvelser løst
- 5.1 Øvelse 1
- 5.2 Øvelse 2
- 6 Referencer
Formler
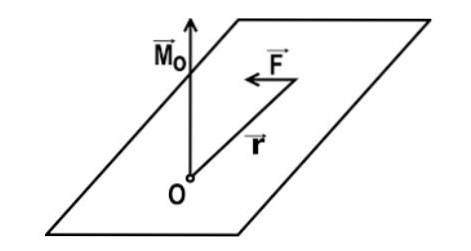
Det matematiske udtryk for drejningsmomentet for en kraft i forhold til et punkt O er givet ved: M = r x F
I dette udtryk er r den vektor, der forbinder punktet O med punktet P for påføring af kraften, og F er vektoren for den påførte kraft.
Momentets måleenheder er N ∙ m, som skønt de er dimensionelt ækvivalente med Joule (J), men har en anden betydning og ikke bør forveksles.
Derfor tager modulets moment moment værdien givet af følgende udtryk:
M = r ∙ F ∙ sin α
I dette udtryk er α vinklen mellem kraftvektoren og vektoren r eller løftearmen. Momentet betragtes som positivt, hvis kroppen roterer mod uret; tværtimod er det negativt, når det drejer med uret.
Enheder
Som allerede nævnt ovenfor er måleenheden for drejningsmoment resultatet af produktet af en kraftenhed og en afstandsenhed. Specifikt bruger det internationale system for enheder den newtonmåler, hvis symbol er N • m.
På et dimensionelt niveau kan newtonmåleren virke svarende til joule; dog må juli under ingen omstændigheder bruges til at udtrykke øjeblikke. Joule er en enhed til måling af værker eller energier, der fra et begrebsmæssigt synspunkt er meget forskellige fra vridningsmomenter.
På samme måde har torsionsmomentet en vektorkarakter, som både er det skalære arbejde og energi.
Egenskaber
Af det, der er set, følger det, at momentet for en kraft i forhold til et punkt repræsenterer kapaciteten af en kraft eller et sæt kræfter til at ændre legemets rotation omkring en akse, der passerer gennem punktet..
Derfor genererer torsionsmomentet en vinkelacceleration på kroppen og er en størrelse af et vektortegn (så det er defineret ud fra et modul, en retning og en følelse), der er til stede i de mekanismer, der er blevet udsat for vridning eller bøjning.
Drejningsmomentet vil være nul, hvis kraftvektoren og vektoren r har samme retning, da værdien af sin α i så fald er nul.
Resulterende drejningsmoment
Givet et bestemt legeme, som en række kræfter virker på, hvis de påførte kræfter virker i samme plan, det drejningsmoment, der er resultatet af anvendelsen af alle disse kræfter; er summen af torsionsmomenter, der skyldes hver kraft. Derfor er det rigtigt, at:
MT = ∑ M = M1 + Mto + M3 +...
Det er selvfølgelig nødvendigt at tage højde for tegnkriteriet for torsionsmomenter, som forklaret ovenfor.
Ansøgninger
Momentet er til stede i applikationer så hver dag som at stramme en møtrik med en skruenøgle, eller åbne eller lukke ethaner eller en dør.
Imidlertid går dens applikationer meget længere; Momentet findes også i maskinens akser eller i resultatet af de bestræbelser, som bjælkerne udsættes for. Derfor er dens applikationer inden for industri og mekanik mange og varierede..

Løst øvelser
Nedenfor er et par øvelser for at lette forståelsen af ovenstående.
Øvelse 1
Givet følgende figur, hvor afstandene mellem punkt O og punkt A og B er henholdsvis 10 cm og 20 cm:
a) Beregn værdien af momentmodulet i forhold til punkt O, hvis der påføres en kraft på 20 N ved punkt A.
b) Beregn, hvad der skal være værdien af den kraft, der påføres i B for at opnå det samme drejningsmoment som opnået i det foregående afsnit.
Opløsning
For det første er det praktisk at overføre dataene til enheder i det internationale system.
rTIL = 0,1 m
rB = 0,2 m
a) For at beregne momentmodulet bruger vi følgende formel:
M = r ∙ F ∙ sin α = 0,1 ∙ 20 ∙ 1 = 2 N ∙ m
b) For at bestemme den krævede styrke skal du fortsætte på en lignende måde:
M = r ∙ F ∙ sin α = 0,2 ∙ F ∙ 1 = 2 N ∙ m
Løsning for F opnås at:
F = 10 N
Øvelse 2
En kvinde udøver en kraft på 20 N på enden af en 30 cm lang skruenøgle. Hvis kraftens vinkel med skruenøglehåndtaget er 30 °, hvad er momentet på møtrikken??
Opløsning
Følgende formel anvendes, og operationen udføres:
M = r ∙ F ∙ sin α = 0,3 ∙ 20 ∙ 0,5 = 3 N ∙ m
Referencer
- Kraftmoment. (nd). På Wikipedia. Hentet den 14. maj 2018 fra es.wikipedia.org.
- Moment (nd). I Wikipedia. Hentet den 14. maj 2018 fra en.wikipedia.org.
- Serway, R. A. og Jewett, Jr. J.W. (2003). Fysik for forskere og ingeniører. 6. udgave Brooks Cole.
- Marion, Jerry B. (1996). Klassisk dynamik af partikler og systemer. Barcelona: Ed. Reverté.
- Kleppner, Daniel; Kolenkow, Robert (1973). En introduktion til mekanik. McGraw-Hill.




Endnu ingen kommentarer