Det ensartet accelereret retlinet bevægelse Det er en, der løber langs en lige linje, og hvor mobilen øger eller formindsker sin hastighed med en konstant hastighed. Denne hastighed er størrelsen, der beskriver den hastighed, hvormed hastigheden ændres og kaldes acceleration.
I tilfælde af ensartet accelereret eller varieret retlinet bevægelse (MRUV) er konstant acceleration ansvarlig for at ændre hastighedens størrelse. I andre typer bevægelser er acceleration også i stand til at ændre retning og følelse af hastighed eller endda bare ændre retning som i ensartet cirkulær bevægelse..
Da acceleration repræsenterer hastighedsændringen over tid, er dens enheder i det internationale system m / sto (meter over sekunder i kvadrat). Ligesom hastighed kan acceleration tildeles et positivt eller negativt tegn, afhængigt af om hastigheden stiger eller falder..
En acceleration på sige +3 m / sto betyder, at for hvert sekund, der går, øges mobilens hastighed med 3 m / s. Hvis mobilens hastighed ved begyndelsen af bevægelsen (ved t = 0) var +1 m / s, så vil den efter et sekund være 4 m / s og efter 2 sekunder vil den være 7 m / s.
I ensartet varieret retlinjet bevægelse tages der højde for de variationer i hastighed, som bevægelige genstande oplever dagligt. Dette er en mere realistisk model end den ensartede retlinede bevægelse. Alligevel er det stadig ret begrænset, da det begrænser mobilen til kun at rejse på en lige linje.
Artikelindeks
Dette er de vigtigste egenskaber ved ensartet accelereret retlinet bevægelse:
-Bevægelse løber altid langs en lige linje.
-Mobilens acceleration er konstant, både i størrelse og i retning og forstand.
-Mobilhastighed stiger (eller falder) lineært.
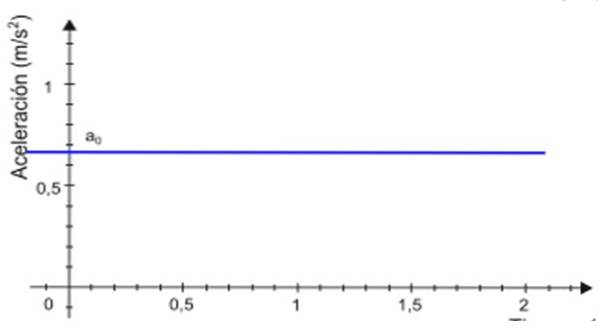
-Siden accelerationen til forbliver konstant over tid t, grafen over dens størrelse som en funktion af tiden er en lige linje. I eksemplet vist i figur 2 er linjen farvet blå, og accelerationsværdien læses på den lodrette akse, ca. +0,68 m / sto.
-Hastighedsgrafen v om t det er en lige linje (i grønt i figur 3), hvis hældning er lig med mobilens acceleration. I eksemplet er hældningen positiv.
-Skæringen med den lodrette akse angiver starthastigheden, i dette tilfælde er den 0,4 m / s.
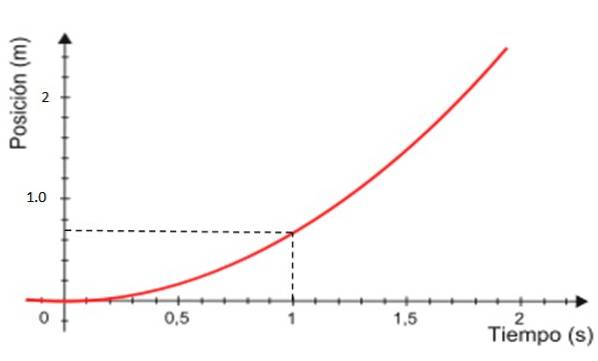
-Endelig er kurven for position x versus tid kurven vist i rødt i figur 4, som altid er en parabel.
Ved at have grafen v vs. t, det er meget let at beregne den tilbagelagte afstand fra mobilen. Den tilbagelagte afstand er lig med området under linjen, der ligger inden for det ønskede tidsinterval.
Antag i det viste eksempel, at du vil vide, hvor lang afstand mobiltelefonen har kørt mellem 0 og 1 sekund. Se figur 5 ved hjælp af denne graf.
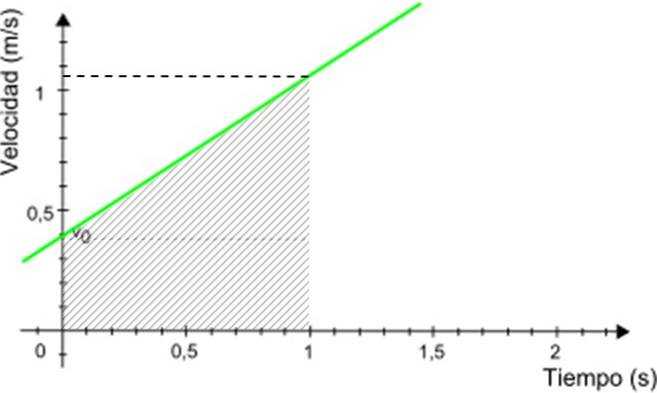
Den ønskede afstand svarer numerisk til det område af trapezformet, der er skraveret i figur 3. Området for trapezoidet er givet ved: (større base + mindre base) x højde / 2
Afstand tilbagelagt = (0,4 + 1,05) x 1/2 m = 0,725 m
Det er også muligt at opdele det skraverede område i en trekant og et rektangel, beregne de tilsvarende områder og tilføje dem sammen. Den tilbagelagte afstand er positiv, selvom partiklen går til højre eller til venstre.
Både den gennemsnitlige acceleration og den øjeblikkelige acceleration har den samme værdi i MRUV, derfor:
-Acceleration: til = konstant
Når accelerationen er lig med 0, er bevægelsen ensartet retlinet, da hastigheden ville være konstant i dette tilfælde. Tegn på til Det kan være positivt eller negativt.
Da accelerationen er hældningen af linjen v versus t, er ligningen v (t):
-Hastighed som en funktion af tiden: v (t) = veller + på
Hvor veller er værdien af mobilens starthastighed
-Position som en funktion af tiden: x (t) = xeller + veller t + ½atto
Når du ikke har tid, men i stedet har hastigheder og forskydninger, er der en meget nyttig ligning, der opnås ved at løse tiden for v (t) = veller + på og erstatte det i den sidste ligning. Er om:
-Ligning, der ikke indeholder tid: vto = vellerto +2.a.Δx
Når man løser en kinematikøvelse, er det vigtigt at sikre sig, at situationen er tilpasset den model, der skal bruges. For eksempel er ligningerne af ensartet retlinet bevægelse ikke gyldige for accelereret bevægelse.
Og de af den accelererede bevægelse er f.eks. Ikke gyldige for en cirkulær eller krumlinjær bevægelse. Den første af disse øvelser løst nedenfor kombinerer to mobiltelefoner med forskellige bevægelser. For at løse det korrekt er det nødvendigt at gå til den relevante bevægelsesmodel.
For at finde ud af dybden af en brønd taber et barn en mønt og aktiverer samtidig sin timer, som stopper lige efter at have hørt mønten ramme vandet. Dens læsning var 2,5 sekunder. Ved at vide, at lydens hastighed i luften er 340 m / s, skal du beregne dybden af brønden.
Være h dybden af brønden. Mønten bevæger sig denne afstand i frit fald, en ensartet varieret lodret bevægelse med starthastighed 0, når mønten falder, og konstant nedadgående acceleration lig med 9,8 m / sto. Tag dig tid tm ved at gøre dette.
Når mønten rammer vandet, bevæger lyden, der forårsages af kliket, opad til barnets øre, som stopper stopuret, når det hører det. Der er ingen grund til at tro, at lydens hastighed ændres, når den stiger op ad brønden, så lydens bevægelse er ensartet retlinet. Lyden tager et stykke tid ts at komme til barnet.
h = ½.g.tm to = 4,9 tm to
Hvor de er blevet udskiftet x Y til af ligningen for positionen, der er givet i det foregående afsnit, af h Y g.
h = vs . ts = 340 ts
Det handler om den velkendte ligning afstand = hastighed x tid. Med disse to ligninger har vi tre ukendte: h, tm og ts. For de tidspunkter, hvor der er et forhold, er det kendt, at alt tager 2,5 sekunder at ske, derfor:
tm + ts = 2,5 sek
Ligning af begge ligninger:
4,9 tm to = 340 ts
Rydde en af gange og erstatte:
4,9 tm to= 340. (2,5 - tm)
Ved at udvikle udtrykket til de rigtige og gennemføre vilkår opnår vi:
4,9 tm to+340 tm - 850 = 0
Dette er en kvadratisk ligning med to løsninger: 2.416 og -71.8. Den positive løsning vælges, hvilket er den, der giver mening, da tiden ikke kan være negativ, og under alle omstændigheder skal den være mindre end 2,5 sekunder. For denne gang opnås det ved at erstatte dybden af brønden:
4,9 tm to= 4,9 x 2,416to m = 28,6 m
En bil, der kører 90 km / t, nærmer sig en gade med trafiklys. Når det er 70 m derfra, tændes det gule lys, som varer i 4 sekunder. Afstanden mellem trafiklyset og det næste hjørne er 50 m.
Føreren har disse to muligheder: a) bremse ved - 4 m / sto eller b) accelerer til + 2 m / sto. Hvilken af de to muligheder giver føreren mulighed for at stoppe eller krydse hele vejen, før lyset bliver rødt?
Førers startposition er x = 0 netop når han ser det gule lys tændes. Det er vigtigt at konvertere enhederne korrekt: 90 km / t svarer til 25 m / s.
I henhold til mulighed a) kører føreren i de 4 sekunder, som det gule lys varer:
x (t) = veller t + ½atto= 25,4 -½. (- 4) .4tom = 68 m (Den stopper 2 meter før trafiklyset)
Analyseringsmulighed b) vi har:
x (t) = veller t + ½atto= 25.t + ½.2.tto
Mens det gule lys varer, kører føreren på denne måde:
x = 25,4 + ½.2.4tom = 116 m
Men 116 m er mindre end den tilgængelige afstand for at komme til det næste hjørne, som er 70 + 50 m = 120 m, derfor kan han ikke krydse hele gaden, før det røde lys tændes. Den anbefalede handling er at bremse og holde sig 2 meter fra trafiklyset.
Folk oplever effekterne af acceleration dagligt: når de kører i bil eller bus, da disse konstant har brug for at bremse og accelerere for at tilpasse hastigheden til forhindringerne på vejen. Acceleration opleves også, når man går op eller ned i en elevator.
Forlystelsesparker er steder, hvor folk betaler for at opleve virkningerne af acceleration og have det sjovt.
I naturen observeres ensartet varieret retlinjet bevægelse, når en genstand falder frit, eller når den smides lodret opad og venter på, at den vender tilbage til jorden. Hvis luftmodstand overses, er accelerationsværdien tyngdekraften: 9,8 m / s2.
Endnu ingen kommentarer