
Euler-metoden, hvad den er til, procedure og øvelser
Det Eulers metode er den mest grundlæggende og enkle af de procedurer, der anvendes til at finde omtrentlige numeriske løsninger til en almindelig differentialligning af første orden, forudsat at dens oprindelige tilstand er kendt.
En almindelig differentialligning (ODE) er ligningen, der relaterer en ukendt funktion af en enkelt uafhængig variabel med dens derivater.
Hvis det største derivat, der vises i ligningen, er af grad 1, er det en almindelig differentialligning af den første grad.
Den mest generelle måde at skrive en ligning af første grad på er:

x = x0
y = y0
Artikelindeks
- 1 Hvad er Eulers metode?
- 2 Løst øvelser
- 2.1 Øvelse 1
- 2.2 Øvelse 2
- 2.3 Øvelse 3
- 3 Newtons dynamik og Eulers metode
- 3.1 Øvelse 4
- 4 Øvelser foreslået til hjemmet
- 4.1 Øvelse 1
- 4.2 Øvelse 2
- 5 Referencer
Hvad er Eulers metode?
Idéen med Eulers metode er at finde en numerisk løsning på differentialligningen i intervallet mellem X0 og XF .
For det første diskretiseres intervallet i n + 1 point:
x0, x1, xto, x3..., xn
Hvilke opnås således:
xjeg= x0+ih
Hvor h er bredden eller trinnet af underintervallerne:

Med den oprindelige betingelse er det også muligt at kende afledningen i starten:
y '(xeller) = f (xeller, Yeller)
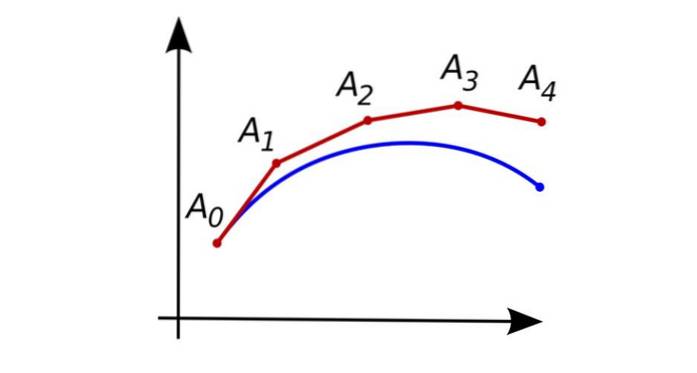
Dette afledte repræsenterer hældningen af tangentlinjen til kurven for funktionen y (x) præcist ved punktet:
Ao = (xeller, Yeller)
Derefter foretages en omtrentlig forudsigelse af værdien af funktionen y (x) på følgende punkt:
y (x1) ≈ og1
Y1 = Yeller +(x1- xeller) f (xeller, Yeller) = ogeller + h f (xeller, Yeller)
Det næste omtrentlige punkt af opløsningen er derefter opnået, hvilket svarer til:
TIL1 = (x1, Y1)
Proceduren gentages for at opnå de successive punkter
TILto, TIL3..., xn
I figuren vist i begyndelsen repræsenterer den blå kurve den nøjagtige opløsning af differentialligningen, og den røde repræsenterer de på hinanden følgende omtrentlige punkter opnået ved Euler-proceduren.
Løst øvelser
Øvelse 1
jeg) Lad differentialligningen være:

Med den oprindelige betingelse x = a = 0; Ytil= 1
Brug Eulers metode til at få en omtrentlig løsning på Y i koordinaten X = b = 0,5, opdeling af intervallet [a, b] i n = 5 dele.
Opløsning

De numeriske resultater er opsummeret som følger:

Fra hvor det konkluderes, at løsningen Y for værdien 0,5 er 1,4851.
Bemærk: for at udføre beregningerne, Smath-studie, gratis at bruge gratis program.
Øvelse 2
II) Fortsæt med differentialligningen fra øvelse I), find den nøjagtige løsning og sammenlign den med resultatet opnået ved Eulers metode. Find fejlen eller forskellen mellem det nøjagtige og omtrentlige resultat.
Opløsning

Den nøjagtige løsning er ikke særlig vanskelig at finde. Afledningen af funktionen sin (x) er kendt for at være funktionen cos (x). Derfor vil løsningen y (x) være:
y (x) = sin x + C
For at den oprindelige betingelse skal være opfyldt, og (0) = 1, skal konstanten C være lig med 1. Det nøjagtige resultat sammenlignes derefter med det omtrentlige:
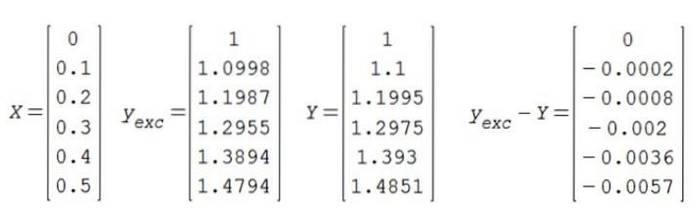
Det konkluderes, at tilnærmelsen i det beregnede interval har tre signifikante præcisionstal.
Øvelse 3
III) Overvej differentialligningen og dens indledende betingelser angivet nedenfor:
y '(x) = - yto
Med den oprindelige betingelse x0 = 0; Y0 = 1
Brug Eulers metode til at finde de omtrentlige værdier af løsningen y (x) i intervallet x = [0, 1,5]. Brug trin h = 0,1.
Opløsning
Eulers metode er meget velegnet til brug sammen med et regneark. I dette tilfælde bruger vi regnearket til geogebra, et gratis og gratis program.
Regnearket i figuren viser tre kolonner (A, B, C), den første er variablen x , den anden kolonne repræsenterer variablen Y, og den tredje kolonne afledt Y '.
Række 2 indeholder de oprindelige værdier for x, Y, Y ' .
Værditrin 0.1 er placeret i den absolutte position celle ($ D $ 4).
Den indledende værdi af y0 er i celle B2, og y1 er i celle B3. For at beregne y1 formlen bruges:
Y1 = Yeller +(x1- xeller) f (xeller, Yeller) = ogeller + h f (xeller, Yeller)
Denne regnearkformel ville være nummer B3: = B2 + $ D $ 4 * C3.
Tilsvarende ville y2 være i celle B4, og dens formel er vist i følgende figur:
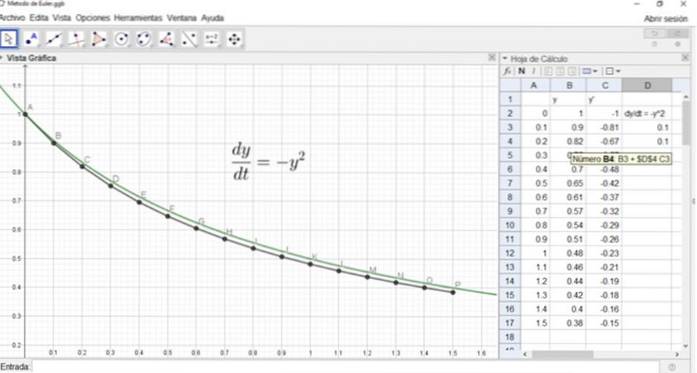
Figuren viser også grafen for den nøjagtige opløsning og punkterne A, B, ..., P for den omtrentlige opløsning efter Eulers metode.
Newtons dynamik og Eulers metode
Klassisk dynamik blev udviklet af Isaac Newton (1643 - 1727). Den oprindelige motivation for Leonard Euler (1707 - 1783) til at udvikle sin metode var netop at løse ligningen af Newtons anden lov i forskellige fysiske situationer.
Newtons anden lov udtrykkes normalt som en differentialligning af anden grad:

Hvor x repræsenterer positionen for et objekt i øjeblikket t. Objektet har en masse m og udsættes for en styrke F. Funktionen F er relateret til kraft og masse som følger:


For at anvende Eulers metode kræves de indledende tidsværdier t, hastighed v og position x.
Den følgende tabel forklarer, hvordan man starter med startværdier t1, v1, x1, en tilnærmelse af hastigheden v2 og positionen x2, i øjeblikket t2 = t1 + Δt, hvor Δt repræsenterer en lille stigning og svarer til trinnet i Eulers metode.

Øvelse 4
IV) Et af de grundlæggende problemer i mekanik er, at en blok af masse M er bundet til en fjeder (eller fjeder) med elastisk konstant K.
Newtons anden lov for dette problem ville se sådan ud:
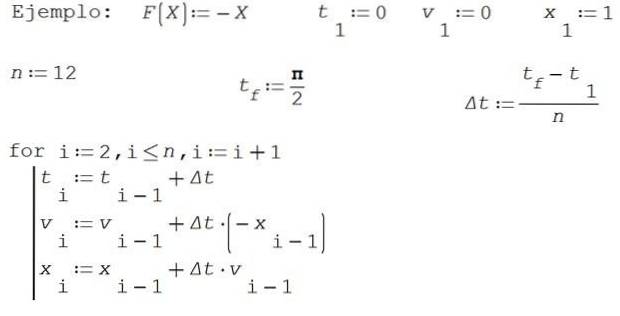
I dette eksempel vil vi for enkelhedens skyld tage M = 1 og K = 1. Find omtrentlige løsninger til position x og hastighed v ved Eulers metode på tidsintervallet [0, π / 2] opdeling af intervallet i 12 dele.
Tag 0 som det første øjeblik, starthastighed 0 og startposition 1.
Opløsning
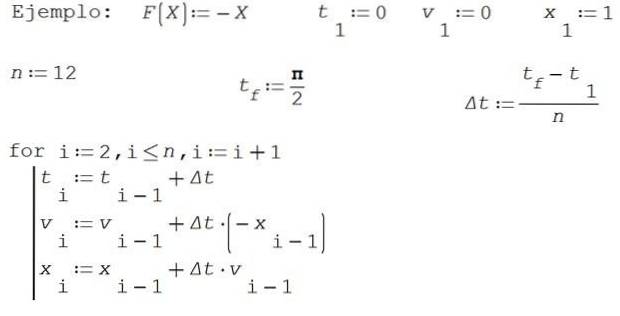
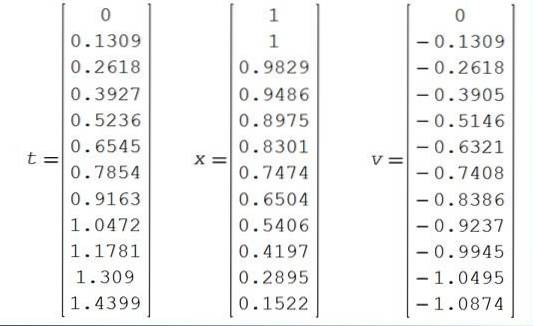
De numeriske resultater er vist i følgende tabel:
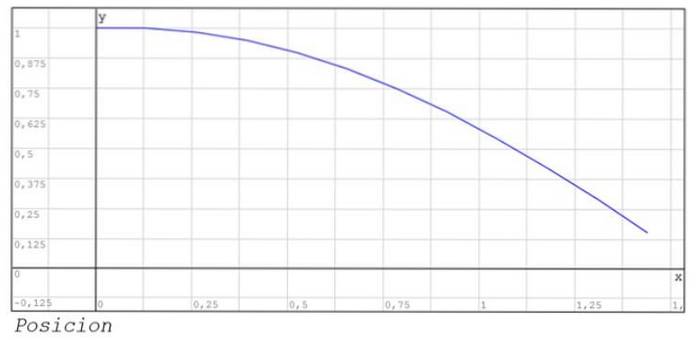
Graferne over position og hastighed mellem øjeblikke 0 og 1,44 er også vist..
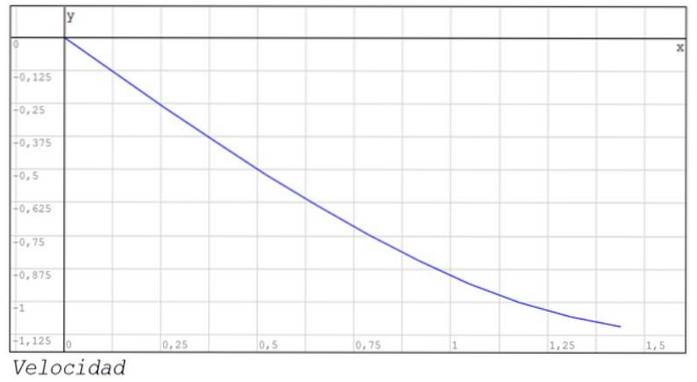
Foreslåede øvelser til hjemmet
Øvelse 1
Brug et regneark til at bestemme en omtrentlig løsning ved hjælp af Eulers metode til differentialligning:
y '= - Exp (-y) med de oprindelige betingelser x = 0, y = -1 i intervallet x = [0, 1]
Start med et 0,1 trin. Plot resultatet.
Øvelse 2
Brug et regneark til at finde numeriske løsninger til følgende kvadratiske ligning, hvor y er en funktion af den uafhængige variabel t.
y "= - 1 / y² med den oprindelige tilstand t = 0; y (0) = 0,5; y '(0) = 0
Find løsningen på intervallet [0,5; 1.0] ved anvendelse af et trin på 0,05.
Plot resultatet: y vs t; y 'vs t
Referencer
- Eurlers metode Hentet fra wikipedia.org
- Euler-løser. Hentet fra en.smath.com



Endnu ingen kommentarer