
Trachtenberg-metoden, hvad den består af, eksempler
Det Trachtenberg-metoden er et system til at udføre aritmetiske operationer, hovedsagelig multiplikation, på en nem og hurtig måde, når dets regler er kendt og mestret.
Det blev udtænkt af den russisk-fødte ingeniør Jakow Trachtenberg (1888-1953), da han var fange af nazisterne i en koncentrationslejr som en form for distraktion for at opretholde sundhed mens han fortsatte i fangenskab..
Artikelindeks
- 1 Hvad det består af, fordele og ulemper
- 2 Eksempler
- 2.1 - Multiplicer et tal med 10 eller med 11
- 2.2 - Multiplikation med tal fra 12 til 19
- 2.3 - Udvidelse af reglerne for multiplikation med 13,… op til 19
- 3 Regler for produkter efter 6, 7 og 5
- 3.1 - Multiplikation med 6
- 3.2 - Multiplikation med 7
- 3.3 - Multiplikation med 5
- 4 Regler for produkter inden 9
- 5 Multiplikation med 8, 4, 3 og 2
- 5.1 - Multiplikation med 8
- 5.2 - Multiplikation med 4
- 5.3 - Multiplikation med 3
- 5.4 - Multiplikation med 2
- 6 Multiplicer med sammensatte tal
- 6.1 Øvelse
- 7 Referencer
Hvad det består af, fordele og ulemper
Fordelen ved denne metode er, at for at udføre multiplikation er det ikke nødvendigt at huske multiplikationstabellerne, i det mindste delvist, er det kun nok at vide, hvordan man tæller og tilføjer, samt at dividere et ciffer med to.
Ulempen er, at der ikke er nogen universel regel for multiplikation med et hvilket som helst tal, snarere varierer reglen alt efter multiplikatoren. Imidlertid er mønstrene ikke vanskelige at huske og tillader i princippet operationer uden hjælp af papir og blyant..
I hele denne artikel vil vi fokusere på reglerne for multiplikation hurtigt.
Eksempler
For at anvende metoden er det nødvendigt at kende reglerne, derfor præsenterer vi dem en efter en og med eksempler:
- Multiplicer et tal med 10 eller med 11
Regel for at multiplicere med 10
-For at gange et tal med 10 skal du blot tilføje et nul til højre. For eksempel: 52 x 10 = 520.
Regler for multiplikation med 11
-Et nul tilføjes til begyndelsen og slutningen af figuren.
-Hvert ciffer tilføjes med sin nabo til højre, og resultatet placeres under det tilsvarende ciffer i den oprindelige figur.
-Hvis resultatet overstiger ni, så noteres enheden, og der placeres en prik på den for at huske, at vi har en enhed, der tilføjes i summen af den næste figur med nabo til højre.
Detaljeret eksempel på multiplikation med 11
Multiplicer 673179 med 11
06731790 x 11 =
--
= 7404969
De nødvendige trin for at nå frem til dette resultat, illustreret med farver, er som følger:
-Enheden af multiplikatorenheden (11) blev ganget med multiplikatorens 9 (0)6731790) og 0 blev føjet til den. Enhedscifret for resultatet blev opnået: 9.
-Derefter multiplicerer vi 1 med 7 og tilføjer ni til 16, og vi bærer 1, vi placerer det ti-cifrede: 6.
-Efter at have ganget 1 med 1, tilføjede naboen til højre 7 plus 1, som han bar, som resultat 9 for hundrede.
-Den næste figur opnås ved at gange 1 med 3 plus naboen 1, det er 4 for tusindcifret.
-Multiplicer 1 med 7, og tilføj nabo 3, hvilket resulterer i 10, placer nul (0) som et ti tusind cifre og tager et.
-Derefter 1 gange 6 plus nabo 7 resultater 13 plus en 1, der havde resultater 14, den 4 som hundrede tusind cifre og tager 1.
-Endelig ganges 1 med det nul, der blev tilføjet i starten, hvilket giver nul plus naboen 6 plus en, der blev båret. Det viser sig endelig 7 for tallet svarende til millioner.
- Multiplikation med tal fra 12 til 19
Sådan multipliceres ethvert tal med 12:
-Et nul tilføjes i starten og et andet nul i slutningen af det tal, der skal ganges.
-Hvert ciffer i figuren, der skal multipliceres, fordobles og tilføjes med nabo til højre.
-Hvis summen overstiger 10, tilføjes en enhed til den næste duplikationsoperation og summen med naboen.
Eksempel på multiplikation med 12
Multiplicer 63247 med 12
0632470 x 12 =
-
758964
Detaljerne for at nå frem til dette resultat, strengt efter de angivne regler, er vist i følgende figur:

- Udvidelse af reglerne for multiplikation med 13, ... op til 19
Metoden til multiplikation med 12 kan udvides til multiplikation med 13, 14 til 19 ved simpelthen at ændre reglen om fordobling ved at tredoble for tilfælde af tretten, firdobling for tilfældet med 14 og så videre, indtil den når 19.
Regler for produkter efter 6, 7 og 5
- Multiplikation med 6
-Tilføj nuller til begyndelsen og slutningen af figuren for at gange med 6.
-Tilføj halvdelen af sin nabo til højre for hvert ciffer, men hvis cifret er ulige, tilføj 5 yderligere.
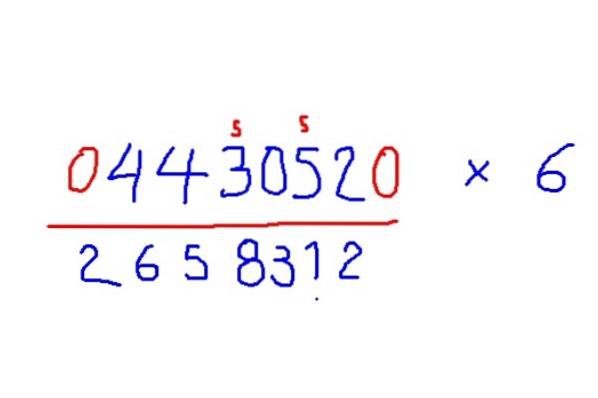
- Multiplikation med 7
-Tilføj nuller til begyndelsen og slutningen af det nummer, der skal multipliceres.
-Dobbelt hvert ciffer og tilføj den nederste hele halvdel af naboen, men hvis cifret er ulige, tilføj derudover 5.
Eksempel på multiplikation med 7
-Multiplicer 3412 med 7
-Resultatet er 23884. For at anvende reglerne anbefales det først at genkende de ulige cifre og placere en lille 5 over dem for at huske at føje denne figur til resultatet..
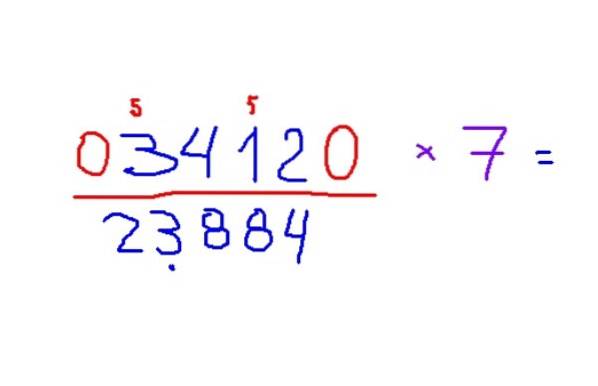
- Multiplikation med 5
-Tilføj nuller til begyndelsen og slutningen af det nummer, der skal multipliceres.
-Placer den nederste helte af naboen under hvert ciffer til højre, men hvis cifret er ulige, skal du tilføje yderligere 5.
Eksempel gang med 5
Multiplicer 256413 med 5
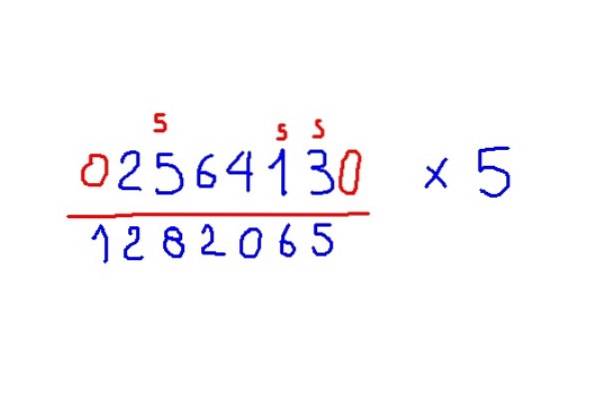
Regler for produkter senest 9
-Et nul tilføjes i begyndelsen, og et andet i slutningen af figuren multipliceres med ni.
-Det første ciffer til højre opnås ved at trække det tilsvarende ciffer af tallet for at gange fra 10.
-Derefter trækkes det næste ciffer fra 9, og naboen tilføjes.
-Det forrige trin gentages, indtil vi når nul i multiplikand, hvor vi trækker 1 fra naboen, og resultatet kopieres til under nul..
Eksempel på multiplikation med 9
Multiplicer 8769 med 9:
087690 x 9 =
--
78921
Operationer
10 - 9 = 1
(9-6) + 9 = 1to (det to og tager 1)
(9-7) + 1 + 6 =9
(9-8) +7 =8
(8-1) = 7
Multiplikation med 8, 4, 3 og 2
-Tilføj nuller til begyndelsen og slutningen af det nummer, der skal multipliceres.
-For det første ciffer fra højre trækkes fra 10, og resultatet fordobles.
-For de følgende cifre trækker vi fra 9, fordobles resultatet, og naboen tilføjes.
-Når du når nul, trækkes 2 fra naboen til højre.
- Multiplikation med 8
Eksempel på multiplikation med 8
-Multiplicer 789 med 8
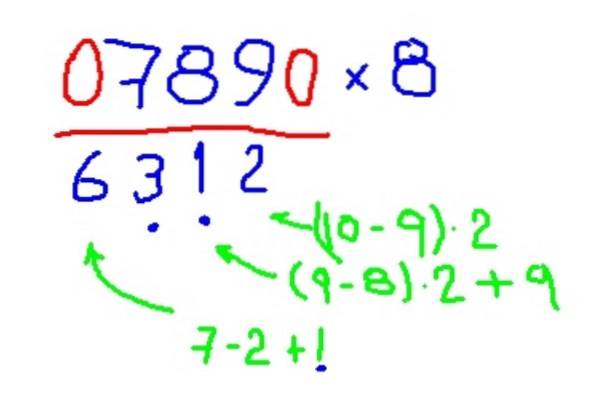
- Multiplikation med 4
-Tilføj nuller til højre og venstre for multiplikatoren.
-Træk det tilsvarende ciffer i enheden fra 10 ved at tilføje 5, hvis det er et ulige ciffer.
-Træk hvert ciffer i multiplikalen fra 9 i formularen, tilføj halvdelen af naboen til højre, og hvis det er et ulige ciffer, tilføj 5 yderligere.
-Når du når nul til begyndelsen af multiplikatoren, skal du placere halvdelen af naboen minus en.
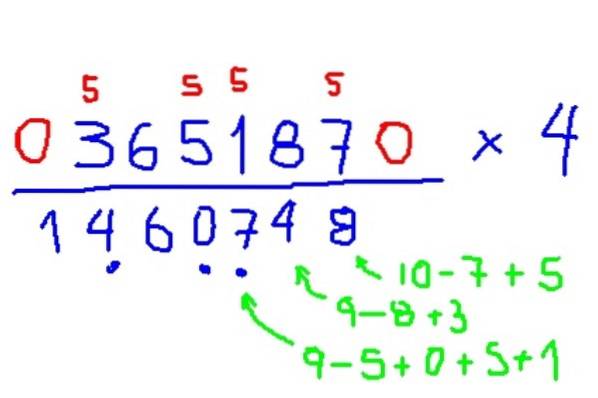
Eksempel på multiplikation med 4
Multiplicer 365187 x 4
- Multiplikation med 3
-Tilføj nul til hver ende af multiplikatoren.
-Træk 10 minus det ene ciffer, og tilføj 5, hvis det er et ulige ciffer.
-For de andre cifre trækker du 9, fordobler resultatet, tilføj halvdelen af naboen og tilføj 5, hvis det er ulige..
-Når du når hovedet nul, skal du placere den nederste heltal halvdel af naboen minus 2.
Eksempel på multiplikation med 3
Multiplicer 2588 med 3

- Multiplikation med 2
-Tilføj nuller i enderne og dobbelt hvert ciffer, hvis det overstiger 10 tilføj et til det næste.
Eksempel gang med 2
Multiplicer 2374 med 2
023740 x 2
04748
Multiplicer med sammensatte tal
Ovennævnte regler gælder, men resultaterne køres til venstre med antallet af steder svarende til tiere, hundreder osv. Lad os se på følgende eksempel:
Dyrke motion
Multiplicer 37654 med 498
0376540 x 498
301232 lineal til 8
338886 regel for 9
150616 lineal til 4
18751692 endelig sum
Referencer
- Cutler, Ann. 1960 Trachtenberg-hastighedssystemet for grundlæggende matematik. Doubleday & CO, NY.
- Dialnet. Hurtigt grundlæggende matematiksystem. Gendannet fra: dialnet.com
- Matematisk hjørne. Hurtig multiplikation ved hjælp af Trachtenberg-metoden. Gendannet fra: rinconmatematico.com
- Trachtenberg Speed System of Basic Mathematics. Gendannet fra: trachtenbergspeedmath.com
- Wikipedia. Trachtenberg-metoden. Gendannet fra: wikipedia.com

Endnu ingen kommentarer