
Konjugere interne og eksterne vinkler eksempler, øvelser
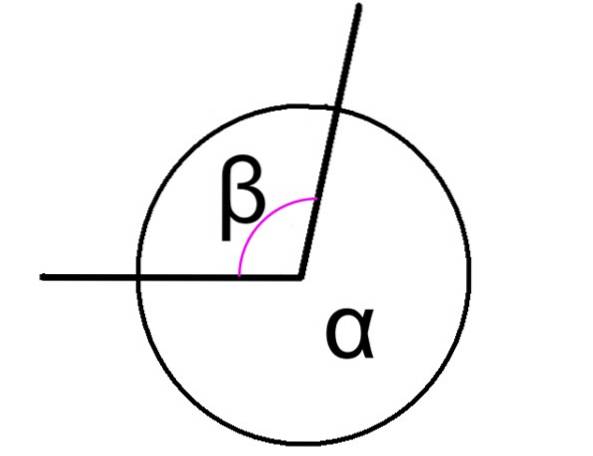
Det konjugerede vinkler Det er dem, der, når de tilføjes, giver 360 ° som et resultat, uanset om disse vinkler er tilstødende eller ej. I figur 1 er to konjugerede vinkler vist, betegnet som α og β.
I dette tilfælde har vinklerne α og β i figuren et fælles toppunkt, og deres sider er fælles, derfor er de tilstødende. Forholdet mellem dem udtrykkes som følger:
α + β = 360 °
På den anden side, lad os nu overveje to parallelle linjer skåret af en sekant, hvis arrangement er vist nedenfor:
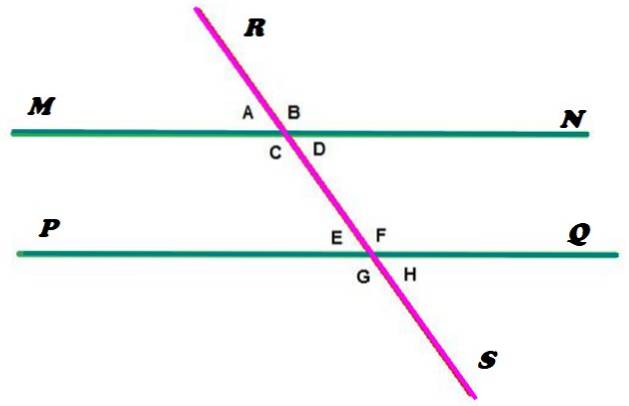
Linjerne MN og PQ er parallelle, mens linjen RS er sekant og skærer parallellerne på to punkter. Som det kan ses, bestemmer denne konfiguration dannelsen af 8 vinkler, der er betegnet med små bogstaver.
I henhold til definitionen givet i starten er vinklerne a, b, c og d konjugeret. Og på samme måde er e, f, g og h, da begge tilfælde er sande:
a + b + c + d = 360º
Y
e + f + g + h = 360º
Til denne konfiguration er to vinkler konjugeret, hvis de er på samme side i forhold til sekantlinjen RS, og begge er interne eller eksterne. I det første tilfælde taler vi om vinkler interne konjugater, mens i det andet er de vinkler eksterne konjugater.
Artikelindeks
- 1 Eksempler
- 2 Indvendige vinkler på en firkant
- 2.1 Eksempler
- 3 Øvelser
- 3.1 - Øvelse 1
- 3.2 - Øvelse 2
- 4 Referencer
Eksempler
I figur 2 er de ydre vinkler dem, der er uden for området afgrænset af linjerne MN og PQ, de er vinklerne A, B, G og H. Mens vinklerne, der ligger mellem de to linjer er C, D, E og F.
Nu er det nødvendigt at analysere, hvilke vinkler der er til venstre og hvilke til højre for sekanten.
Til venstre for RS er vinklerne A, C, E og G. Og til højre er vinklerne B, D, F og H.
Vi fortsætter straks med at bestemme de konjugerede vinkelpar i henhold til definitionen i det foregående afsnit:
-A og G, udvendigt og til venstre for RS.
-D og F, internt og til højre for RS.
-B og H, udvendigt og til højre for RS.
-C og E, internt og til venstre for RS.
Ejendom af konjugerede vinkler mellem parallelle linjer
De konjugerede vinkler mellem parallelle linjer er supplerende, dvs. deres sum er lig med 180º. På denne måde gælder følgende for figur 2:
A + G = 180º
D + F = 180º
B + H = 180º
C + E = 180 °
Par med tilsvarende vinkler til parallelle linjer
Det er dem, der er på samme side af sekantlinjen, de er ikke tilstødende, og den ene er intern og den anden er ekstern. Det er vigtigt at visualisere dem, da deres mål er den samme, fordi de er modsatte vinkler ved toppunktet.
Når vi vender tilbage til figur 2, identificeres de tilsvarende vinkelpar som:
-A og E
-C og G
-B og F
-D og H
Indvendige vinkler af en firkant
Kvadrilaterale er 4-sidede polygoner, blandt andet firkanten, rektanglet, trapezformen, parallelogrammet og romben. Uanset deres form er det rigtigt, at summen af deres indre vinkler er 360 ° i nogen af dem, derfor opfylder de den definition, der blev givet i starten..
Lad os se nogle eksempler på firkanter og hvordan man beregner værdien af deres interne vinkler i henhold til oplysningerne i de foregående afsnit:
Eksempler
a) Tre af vinklerne på et firkantet mål 75º, 110º og 70º. Hvor meget skal den resterende vinkel måle?
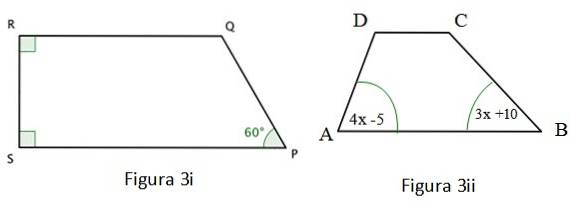
b) Find værdien af vinklen ∠Q i figur 3 i.
c) Beregn målingen for vinklen ∠A i figur 3 ii.
Løsning til
Lad α være den manglende vinkel, det er tilfreds med at:
α + 75º + 110º + 70º = 360º → α = 105º
Løsning b
Figur 3i er vist a trapesformet og to af dens indvendige vinkler er rigtige, som er markeret med en farvet firkant i hjørnerne. For denne firkant er følgende verificeret:
∠R + ∠S + ∠P + ∠Q = 360º; ∠S = ∠R = 90 °; ∠P = 60º
Derfor:
∠ Q = 2 x 90º + 60º = 240º
Løsning c
Kvadrilateralen i figur 3 ii er også en trapezform, for hvilken følgende er sandt:
∠A + ∠B + ∠C + ∠D = 360º
Derfor:
4x -5 + 3x + 10 +180 = 360
7x + 5 = 180
x = (180 - 5) / 7
x = 25
For at bestemme den vinkel, der kræves i udsagnet, bruger vi, at ∠A = 4x - 5. Ved at erstatte den tidligere beregnede værdi af x følger det, at ∠A = (4 × 25) -5 = 95º
Uddannelse
- Øvelse 1
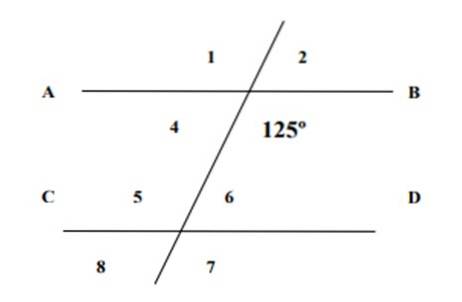
Ved at vide, at en af de viste vinkler er 125º, skal du finde målingerne af de 7 resterende vinkler i den følgende figur og retfærdiggøre svarene.
Opløsning
Vinkel 6 og vinkel 125º er indvendige konjugater, hvis sum er 180º i henhold til egenskaberne af konjugerede vinkler, derfor:
∠6 + 125º = 180º → ∠6 = 180º - 125º = 55º
På den anden side er ∠6 og ∠8 modsatte vinkler ved toppunktet, hvis mål er det samme. Derfor måler ∠8 55º.
Vinklen ∠1 er også modsat af toppunktet ved 125 º, så kan vi bekræfte, at ∠1 = 125 º. Vi kan også appellere til det faktum, at de tilsvarende par vinkler har samme mål. I figuren er disse vinkler:
∠7 = 125 º
∠2 = ∠6 = 55 º
∠1 = ∠5 = 125º
∠4 = ∠8 = 55 º
- Øvelse 2
Find værdien af x i følgende figur og værdierne for alle vinklerne:
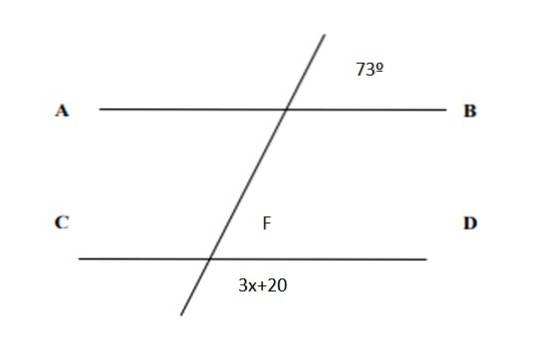
Opløsning
Da de er tilsvarende par, følger det, at F = 73º. Og på den anden side er summen af de konjugerede par 180º, derfor:
3x + 20º + 73º = 180º
3x = 180º - 73º -20º = 87
Endelig er værdien af x:
x = 87/3 = 29
Hvad angår alle vinklerne, er de anført i følgende figur:
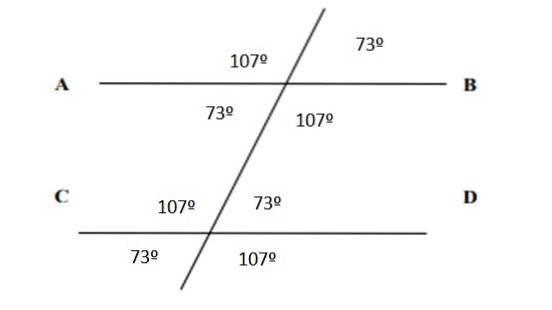
Referencer
- Vinkelgrupper. Supplerende, supplerende og supplerende vinkler Forklaring. Gendannet fra: thisiget.com/
- Baldor, A. 1983. Plane- og rumgeometri og trigonometri. Patria Cultural Group.
- Corral, M. Mathematics LibreTexts: Angles. Gendannet fra: math.libretexts.org.
- Mathmania. Klassificering og konstruktion af vinkler efter deres måling. Gendannet fra: mathematania.com/
- Wentworth, G. Plane Geometry. Gendannet fra: gutenberg.org.
- Wikipedia. Konjugerede vinkler. Gendannet fra: es.wikipedia.org.



Endnu ingen kommentarer