Vinkler i omkredsstyper, egenskaber, løste øvelser

Hedder omkredsvinkler dem, hvor nogle af dets elementer er eller krydser hinanden ved en given omkreds. Blandt dem er følgende:

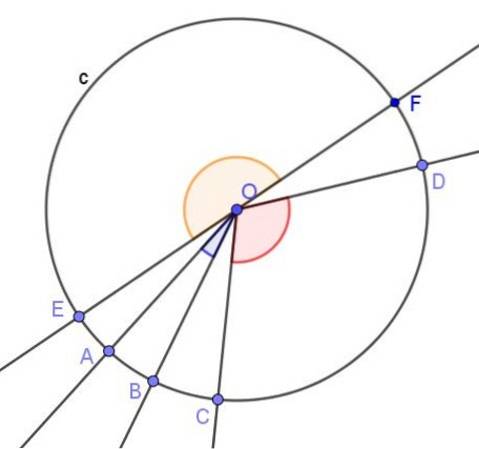
1. - Den central vinkel, hvis toppunkt er i midten af ​​omkredsen, og dens sider er sekant for det, som vi ser på følgende billede:

2. - Den indskrevet vinkel, hvis toppunkt er på omkredsen, og dens sider er sekant eller tangent til omkredsen.

3.- Udenfor vinkel, hvis toppunkt er uden for omkredsen, men dets sider er sekant eller tangent til omkredsen.

4.- Den indvendig vinkel, med toppunktet inde i omkredsen og dets sider er skille til det.

Alle disse vinkler har visse forhold til hinanden, og dette fører os til vigtige egenskaber mellem de vinkler, der hører til en given cirkel.

Artikelindeks

• 1 egenskaber
  • 1.1 - Central vinkel
  • 1.2 - Indskrevet vinkel
  • 1.3 - Udvendig vinkel
  • 1.4 - Indvendig vinkel
• 2 Løst øvelser
  • 2.1 - Øvelse 1
  • 2.2 - Øvelse 2
• 3 Referencer

Ejendomme

- Central vinkel

Den centrale vinkel er defineret som den, hvis toppunkt er i midten af ​​omkredsen, og dens sider skærer omkredsen.

Målingen i radianer af en central vinkel er kvotienten mellem den nedadgående bue, det vil sige buen af ​​omkredsen mellem siderne af vinklen og radius af omkredsen. 

Hvis omkredsen er enhed, det vil sige med radius 1, er målingen af ​​den centrale vinkel længden af ​​buen, hvilket svarer til antallet af radianer.

Hvis du vil have et mål for den centrale vinkel i grader, skal du multiplicere målet i radianer med faktoren 180º / π.

Vinkelmåleinstrumenter, såsom vinkelmåler og goniometer, bruger altid en central vinkel og længden af ​​den udskårne bue.

De er kalibreret i kønssimale grader, hvilket betyder, at når en vinkel måles med dem, i baggrunden, hvad der måles, er længden af ​​buen, der er undertrykket af den centrale vinkel.

Ejendom

Målingen for en central vinkel i radianer er lig med længden af ​​den nedadgående eller opsnappende bue divideret med længden af ​​radius.

- Indskrevet vinkel

Den indskrevne vinkel på en cirkel er en, der har sin toppunkt på omkredsen, og dens stråler er sekant eller tangent til den.. 

Dens egenskaber er:

Ejendomme

-Den indskrevne vinkel er konveks eller plan.

-Når en indskrevet vinkel skærer den samme bue som den centrale vinkel, vil målene for den første vinkel være halvdelen af ​​den anden..

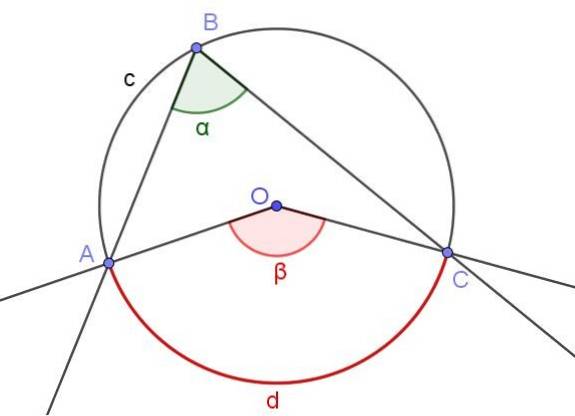
Figur 3 viser to vinkler ∠ABC og ∠AOC, der skærer den samme bue af omkredsen A⌒C.

Hvis målingen for den indskrevne vinkel er α, så er målingen β for den centrale vinkel dobbelt så stor som den indskrevne vinkel (β = 2 α), fordi begge understreger den samme bue af måling d.

- Udenfor vinkel

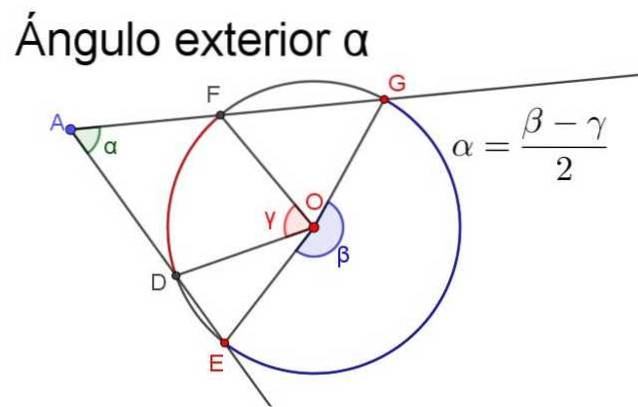
Det er den vinkel, hvis toppunkt er uden for omkredsen, og hver af dens sider skærer omkredsen på et eller flere punkter.

Ejendom

-Dens mål er lig med halvforskellen (eller forskellen divideret med 2) af de centrale vinkler, der opfanger de samme buer.

For at sikre, at målingen er positiv, skal semi-forskellen altid være den for den største centrale vinkel minus målingen for den mindste centrale vinkel, som illustreret i den følgende figur.

- Indre vinkel

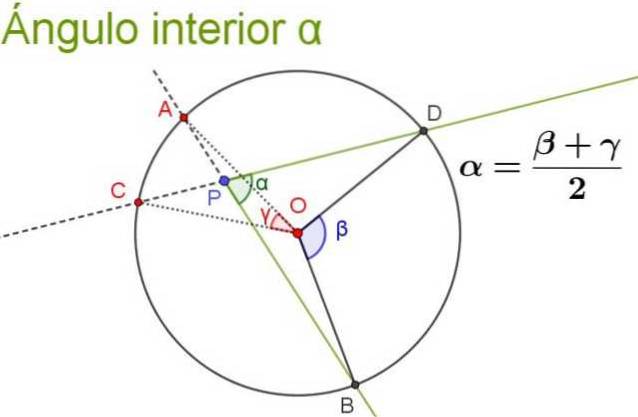
Den indvendige vinkel er den, hvis toppunkt er inden i omkredsen, og dens sider skærer omkredsen.

Ejendom 

Dens mål er lig med halvsummen af ​​den centrale vinkel, der undergraver den samme bue, plus den centrale vinkel, der dækker den samme bue som dens forlængelsesvinkel (dette er den indvendige vinkel dannet af strålerne supplerende med den oprindelige indvendige vinkel ).

Følgende figur illustrerer og tydeliggør egenskaben ved den indvendige vinkel.

Løst øvelser

- Øvelse 1

Antag en indskrevet vinkel, hvor en af ​​dens sider passerer gennem midten af ​​cirklen, som vist i figur 6. Cirkelens radius er OA = 3 cm, og buen d har en længde på π / 2 cm. Bestem værdien af ​​vinklerne α og β.

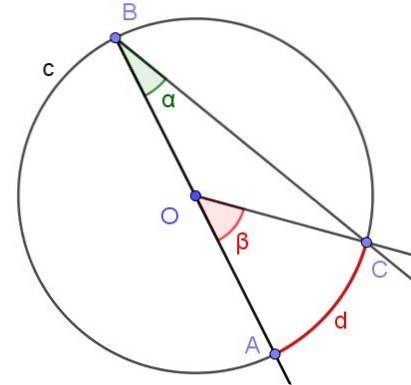
Opløsning

I dette tilfælde dannes den ligebenede trekant COB, da [OC] = [OB]. I en ensartet trekant er vinklerne ved siden af ​​basen ens, derfor er ∠BCO = ∠ABC = α. På den anden side ∠COB = 180º - β. I betragtning af summen af ​​de interne vinkler i trekanten COB har vi:

α + α + (180 º - β) = 180 º

Heraf følger, at 2 α = β, eller hvad der er ækvivalent α = β / 2, hvormed egenskaben (3) i det foregående afsnit er bekræftet, at målingen af ​​den indskrevne vinkel er halv den centrale vinkel, når begge vinkler undertryk den samme akkord [AC].

Nu fortsætter vi med at bestemme de numeriske værdier: vinklen β er central, og dens mål i radianer er kvotienten mellem buen d og radiusen r = OA, så dens mål er:

β = d / r = (π / 2 cm) / (3 cm) = π / 6 rad = 30 º.

På den anden side var det allerede blevet sagt, at α = β / 2 = (π / 6 rad) / 2 = π / 12 rad = 15º. 

- Øvelse 2

I figur 7 er vinklerne α₁ og β_to de har samme mål. Desuden er vinklen β₁ måler 60º. Bestem vinklerne β og α.

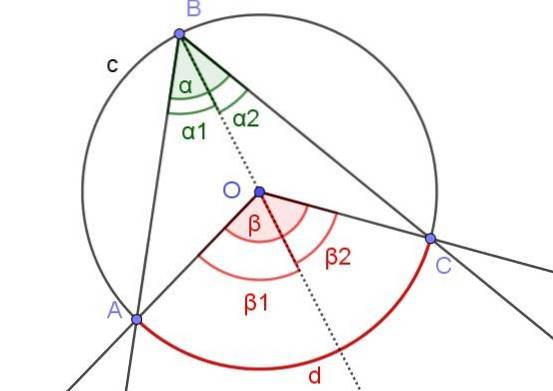
Opløsning

I dette tilfælde har vi en indskrevet vinkel ∠ABC, hvor centrum O af omkredsen er inden for vinklen.

På grund af egenskaben (3) har vi α_to = β_to / 2 og α₁ = β₁ /to. Hvad:

α = α₁ + a_to og β = β₁ + β_to

Derfor følger det, at:

α = α₁ + a_to = β₁ / 2 + β_to / 2 = (β₁ + β_to) / 2 = β / 2.

I henhold til egenskaberne:

α = β / 2

Da vi får at vide, at β₁ = 60º derefter:

a₁ = β₁ / 2 = 60º / 2 = 30º.

De fortæller os også, at α₁ = β_to så det følger, at:

β_to = 30º.

Vinklen β resulterer:

β₁ + β_to = 60º + 30º = 90º.

Og da α = β / 2, så:

α = 90º / 2 = 45º. 

Afslutningsvis:

β = 90º og α = 45º.

Referencer

1. Baldor, A. 1973. Geometri og trigonometri. Centralamerikansk kulturforlag.
2. E. A. 2003. Elementer af geometri: med øvelser og kompasgeometri. University of Medellin.
3. Geometri 1. ESO. Vinkler på omkredsen. Gendannet fra: edu.xunta.es.
4. Al videnskab. Løst problemer med vinkler i omkredsen. Gendannet fra: francesphysics.blogspot.com
5. Wikipedia. Indskrevet vinkel. Gendannet fra: es.wikipedia.com