
Vinkler modsat af Vertex (med øvelse løst)
Det Modsatte vinkler ved toppunktet er dem, der opfylder følgende: siderne på en af dem er forlængelserne af siderne i den anden vinkel. Det grundlæggende sætning af de vinkler, der er modsat af toppunktet, siger sådan: to vinkler modsat af toppunktet har samme mål.
Sprog misbruges ofte ved at sige, at vinklerne over for toppunktet er ens, hvilket ikke er korrekt. Bare fordi to vinkler har samme mål, betyder det ikke, at de er ens. Det er som at sige, at to børn i samme højde er ens.
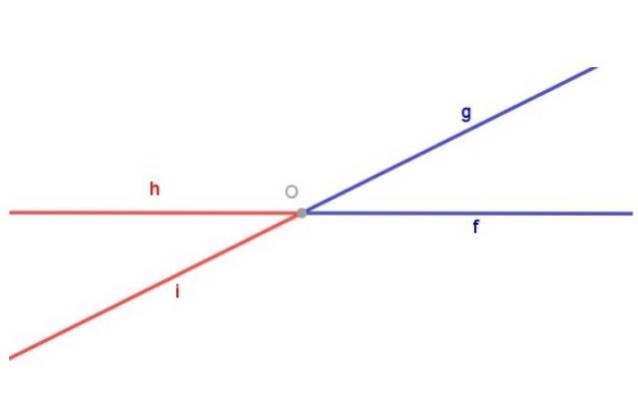
Husk at en vinkel er defineret som den geometriske figur sammensat af to stråler med samme oprindelse.
Figur 1 viser vinklen tåge (blå) sammensat af strålen [Af) og strålen [Og) af fælles oprindelse ELLER. Figur 1 viser også vinklen hej (rød) sammensat af strålen [Jeg hørte) og strålen [Åh) begge med oprindelse ELLER.
To vinkler modsat toppunktet er to forskellige geometriske figurer. For at fremhæve dette er vinklen i figur 1 blevet farvet tåge blå, mens vinklen hej er blevet rødfarvet.
De blå og røde vinkler i figur 1 er modsatte ved toppunktet, fordi: strålen [Af) af den blå vinkel er strålens forlængelse [Åh) af den røde vinkel og strålen [Og) af den blå vinkel er strålingens forlængelse [Jeg hørte) af den røde vinkel.
Artikelindeks
- 1 Vigtige begreber om vinkler
- 1.1 Sider og hjørner af en vinkel
- 1.2 Vinkler dannet af to skæringslinjer
- 2 vinkelrette linjer og ret vinkel
- 2.1 Stråler på samme linje og plan vinkel
- 2.2 Nul vinkel og fuld vinkel
- 3 Vinkelmåling
- 3.1 Sexagesimalt system
- 4 Vertex Angles Theorem
- 4.1 Demo
- 5 Øvelse løst
- 5.1 Løsning
- 6 Referencer
Vigtige begreber om vinkler
Sider og hjørner af en vinkel
Den geometriske figur, der består af to stråler med fælles oprindelse, er en vinkel. Det følgende billede viser vinklen POQ dannet af de to stråler [OP) Y [OQ] af fælles oprindelse ELLER:
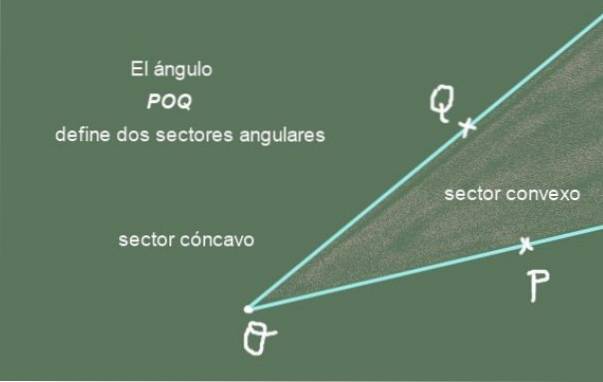
Strålerne [OP) Y [OQ] er de vinkelsider POQ, mens det fælles punkt O kaldes vinkel toppunkt.
Vinkelsektor: En vinkel deler planet, der indeholder det, i to vinkelsektorer. En af dem er den konvekse vinkelsektor og den anden er den konkave vinkelsektor. Foreningen af de to sektorer giver det komplette plan.
Figur 2 viser vinklen POQ og dets to vinklede sektorer. Den konvekse vinkelsektor er den med en spids form, mens den konkave er den vinkelsektor af det plan, der mangler den konvekse sektor.
Vinkler dannet af to linjer, der krydser hinanden
To krydsende linjer i et plan danner fire vinkler og deler planet i fire vinkelsektorer.
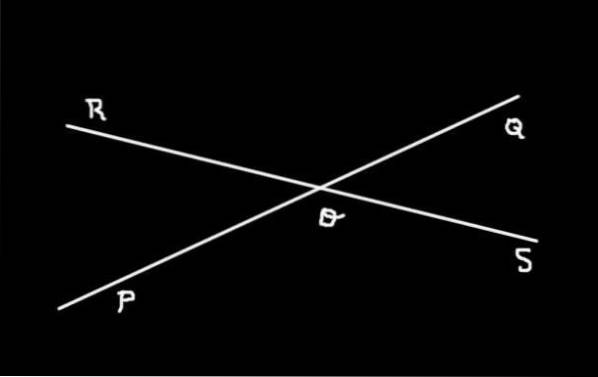
Figur 3 viser de to linjer (PQ) Y (RS) der opfanges i ELLER. Der kan det ses, at fire vinkler bestemmes:
-SOQ, QOR, ROP Y POS
Vinklerne SOQ Y QOR, QOR Y ROP, ROP Y POS, POS Y SOQ De er tilstødende vinkler hinanden, mens SOQ Y ROP de er modsatte i toppen. Det er de også Modsatte vinkler ved toppunktet Vinklerne QOR Y POS.
Vinkelrette linjer og rette vinkler
To secant linjer (krydsende linjer) er Vinkelrette lige linjer hvis de bestemmer fire vinkelsektorer med lige mål. Hvis hver af de fire sektorer er symmetriske med den tilstødende vinkelsektor, har de samme mål.
Hver af de vinkler, der bestemmer de to vinkelrette linjer, kaldes ret vinkel. Alle rette vinkler har samme mål.
Stråler på samme linje og plan vinkel
Med en linje og et punkt på den defineres to stråler. Disse to stråler definerer to plane vinkler.
I figur 3 kan du se linjen (RS) og pointen ELLER som hører til (RS). Vinklen SOR er en plan vinkel. Det kan også siges, at vinklen ROS er en plan vinkel. Alle plane vinkler har samme mål.
Nul vinkel og fuld vinkel
En enkelt stråle definerer to vinkler: den ene af den konvekse vinkelsektor er den null vinkel og den anden, at den konkave vinkelsektor er fuld vinkel. I figur 3 kan du se null vinkel SOS og fuld vinkel SOS.
Vinkelmåling
Der er to nummersystemer, der ofte bruges til at angive et mål for en vinkel.
En af dem er det seksagesimale system, det vil sige baseret på tallet 60. Det er en arv fra de gamle mesopotamiske kulturer. Det andet system for vinkelmåling er radiansystemet, baseret på antallet π (pi) og er en arv fra de antikke græske vismænd, der udviklede geometri.
Sexagesimalt system
Nul vinkel: i sexagesimal-systemet måler nulvinklen 0º (nul grader).
Fuld vinkel: det tildeles mål 360º (tre hundrede og tres grader).
Planvinkel: i sexagesimal-systemet måler planvinklen 180º (hundrede og firs grader).
Ret vinkel: to vinkelrette linier deler planet i fire vinkler med lige mål kaldet retvinkler. Mål for en ret vinkel er den fjerde del af den komplette vinkel, det vil sige 90º (halvfems grader).
Vinkelmåler eller goniometer
Vinkelmåleren er det instrument, der bruges til at måle vinkler. Den består af en halvcirkel (normalt klar plast) opdelt i 180 vinklede sektioner. Da en halvcirkel danner en plan vinkel, er målingen mellem to på hinanden følgende sektioner 1º.
Goniometeret ligner vinkelmåleren og består af en cirkel opdelt i 360 vinklede sektioner.
En vinkel, hvis sider starter fra midten af goniometeret skærer to sektorer, og målene for denne vinkel i grader er lig med antallet af sektioner mellem de to opfangede sektorer, i dette tilfælde vil målingen være nº (det lyder "Jan grader”).
Vertex Angles Theorem
Formelt angives sætningen på denne måde:
Hvis to vinkler er lodret modsatte, har de samme mål.
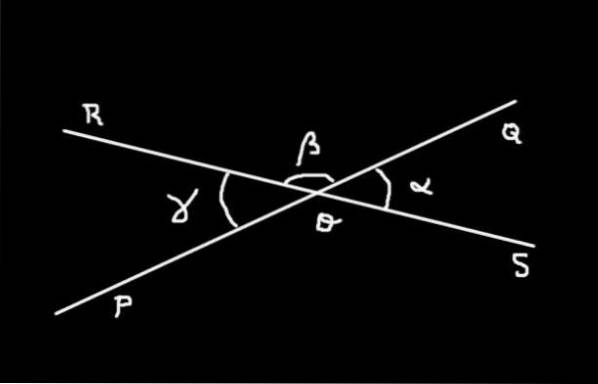
Demonstration
Vinklen SOQ har mål α; vinklen QOR har mål β og vinkel ROP har mål γ. Summen af vinklen SOQ mere ham QOR danner den plane vinkel SOR måler 180º.
Det er:
α + β = 180º
På den anden side og bruger samme ræsonnement med vinklerne QOR Y ROP du har:
β + γ = 180º
Hvis vi observerer de to foregående ligninger, er den eneste måde, hvorpå begge opfyldes, at α er lig med γ.
Hvad SOQ har mål α og er modsat af toppunktet til ROP af måling γ, og da α = γ, konkluderes det, at vinklerne overfor toppunktet har samme mål.
Træning løst
Idet der henvises til figur 4: Antag at β = 2 α. Find målene for vinklerne SOQ, QOR Y ROP i sexagesimal grader.
Opløsning
Som summen af vinklen SOQ mere ham QOR danner den plane vinkel SOR du har:
α + β = 180º
Men de fortæller os, at β = 2 α. Ved at erstatte denne værdi af β har vi:
α + 2 α = 180º
Nemlig:
3 α = 180º
Hvilket betyder, at α er den tredje del af 180º:
α = (180º / 3) = 60º
Så måling af SOQ er α = 60º. Mål for QOR er β = 2 α = 2 * 60º = 120º. Endelig som ROP er modsat af vertex til SOQ så ifølge den allerede bevist sætning har de samme mål. Det vil sige mål for ROP er γ = α = 60º.
Referencer
- Baldor, J. A. 1973. Plane and Space Geometry. Centralamerikansk kultur.
- Matematiske love og formler. Vinkelmålesystemer. Gendannet fra: ingemecanica.com.
- Wikipedia. Modsatte vinkler ved toppunktet. Gendannet fra: es.wikipedia.com
- Wikipedia. Transportør. Gendannet fra: es.wikipedia.com
- Zapata F. Goniómetro: historie, dele, drift. Gendannet fra: lifeder.com


Endnu ingen kommentarer