Det Froude nummer i hydraulik angiver det forholdet, der eksisterer mellem de inertiale kræfter og tyngdekrafterne for en væske. Derfor er det en måde at betegne følgende kvotient på:
HvorF er betegnelsen for Froude-nummeret, en dimensionsløs mængde givet dette navn til ære for den bemærkelsesværdige britiske flådearkitekt og hydraulikingeniør William Froude (1810-1879). Froude og hans søn eksperimenterede ved at trække flade ark gennem vandet for at estimere bådens modstand mod bølger.
I handling af bølgerne forårsaget af en båd under sejlads eller strømmen på en søjle af broen er inertikræfterne og tyngdekraften til stede.
Froude-nummeret er særlig vigtigt i karakteriseringen af væskestrøm i en åben kanal. Et åbent rør eller en kanal er en ledning, hvis øvre overflade er åben for atmosfæren. Eksempler findes i overflod i naturen i form af floder og vandløb.
Og i menneskeskabte konstruktioner har vi:
-Render og afløb i gader og bygninger til ledning af regnvand.
-Grøfter til kunstvanding.
-Deponier og afløb.
-Kølekanaler til industrimaskiner.
Alt dette er eksempler på rør, der er åbne for atmosfæren, hvor Froude-nummeret altid skal tages i betragtning, når flowet karakteriseres..
Artikelindeks
Kvotienten, der blev angivet i begyndelsen, mellem inertikræfterne og tyngdekraften, har følgende form afhængigt af væskens parametre:
Den forrige ligning eller kvadratroden er Froude-nummeret:
Som forklaret i starten er strømmen af vand gennem kanaler, der er åbne for atmosfæren, meget hyppig. I disse tilfælde udføres beregningen af Froude-nummeret ved at anvende følgende formel:
NF = v / (gyh) ½
Hvor Yh er den hydrauliske dybde, v er den gennemsnitlige strømningshastighed og g er værdien af accelerationen på grund af tyngdekraften. Til gengæld beregnes den hydrauliske dybde som følger:
Yh = A / T
I denne formel repræsenterer A nettotværsnitsarealet, og T er bredden af den frie overflade af væsken, den, der udsættes for atmosfæren, øverst på kanalen eller røret. Det gælder for en rektangulær kanal eller en, der er bred nok og med konstant dybde.
Det er vigtigt at fremhæve det faktum, at da NF er dimensionsløs, så er produktet gyh det skal være kvadratet af en hastighed. Det kan faktisk vises, at:
cellerto = gyh
Med celler som formeringshastigheden for en overfladebølge, analog med lydhastigheden i en væske. Derfor er Froude-nummeret også analogt med Mach-nummeret, der ofte bruges til at sammenligne flyhastigheden med lydens..
Væskeflow i en åben kanal klassificeres i tre regimer i henhold til værdien af NF:
-Når nF < 1, se tiene un movimiento en régimen lento o subkritisk.
-UdenF = 1 flowet er navngivet kritisk flow.
-Endelig hvis du har NF > 1 bevægelsen udføres i hurtig eller superkritisk.
Reynolds nummer NR er en anden dimensionsløs størrelse, der er meget vigtig i analysen af væskestrøm, hvorved det er kendt, når væsken har opførsel laminat og hvornår er det turbulent. Disse begreber gælder både for lukkede rør og åbne kanalstrømme..
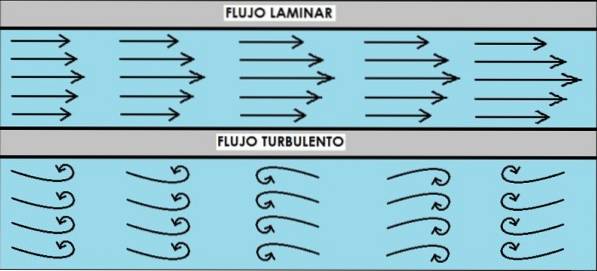
En strømning er laminær, når væsken bevæger sig jævnt og ordentligt i lag, der ikke blandes. På den anden side er den turbulente strøm karakteriseret ved at være kaotisk og uordnet.
En måde at finde ud af, om en vandstrøm er laminær eller turbulent, er ved at injicere en strøm af blæk. Hvis strømmen er laminær, strømmer blækstrømmen adskilt fra vandets, men hvis det er en turbulent strøm, blander blanden sig hurtigt og forsvinder i vandet.
I denne forstand har vi, når vi kombinerer virkningerne af Froude-nummeret med de af Reynolds-nummeret:
-Subkritisk laminar: NR < 500 y NF < 1
-Turbulent subkritisk: NR > 2000 og NF < 1
-Superkritisk laminar: NR < 500 y NF > 1
-Superkritisk turbulent: NR > 2000 og NF > 1
Når strømme forekommer i overgangsregionerne, er det sværere at karakterisere dem på grund af deres ustabilitet.
En flod, der er 4 m bred og 1 m dyb, har en strøm på 3 m3 / s. Find ud af om strømmen er subkritisk eller superkritisk.
For at finde værdien af NF det kræves at kende hastigheden på flodstrømmen. Erklæringen giver os strømningshastigheden, også kendt som volumenstrømningshastigheden, som afhænger af tværsnitsarealet og hastigheden v af strømningen. Det beregnes således:
Q = A.v
Hvor Spørgsmål er strømmen, TIL er tværsnitsarealet og v er hastigheden. Antages et rektangulært tværsnitsareal:
A = bredde x dybde = 4 m x 1 m = 4 mto
Derefter er hastigheden v:
v = Q / A = 3 m3 / s / 4 mto= 0,75 m / s
Den hydrauliske dybde i tilfældet med det rektangulære sektionsrør falder sammen med dybden og erstatter derfor værdier i ligningen for NF, med Yh = 1 m Y g = 9,8 m / sto du har:
NF = v / (gyh) ½ = 0,75 m / s / (9,8 m / sto x 1m) ½ = 0,24
Da NF er mindre end 1, har strømmen en subkritisk adfærd, dvs. langsom.
Endnu ingen kommentarer