Det sammensatte tal er de heltal, der har mere end to delere. Hvis vi ser nøje, er alle tal i det mindste delelige nøjagtigt af sig selv og af 1. De, der kun har disse to skillevægge, kaldes primtal, og dem, der har mere, er forbindelser..
Lad os se på tallet 2, som kun kan deles mellem 1 og 2. Nummeret 3 har også to skillevægge: 1 og 3. Derfor er de begge primære. Lad os nu se på tallet 12, som vi kan dele nøjagtigt med 2, 3, 4, 6 og 12. Ved at have 5 delere er 12 et sammensat tal.
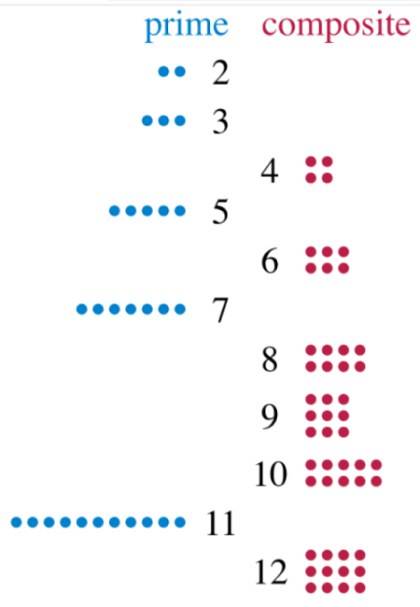
Og hvad sker der med tallet 1, det der deler alle de andre? Nå, det er ikke prime, fordi det ikke har to skillevægge, og det er ikke sammensat, derfor falder 1 ikke i nogen af disse to kategorier. Men der er mange, mange flere tal, der gør..
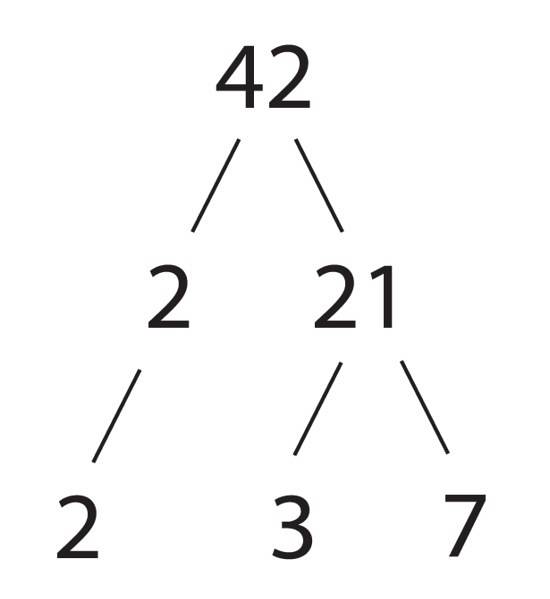
Sammensatte tal kan udtrykkes som produktet af primtal, og dette produkt, bortset fra rækkefølgen af faktorerne, er unikt for hvert nummer. Dette sikres ved den grundlæggende sætning af aritmetik bevist af den græske matematiker Euklid (325-365 f.Kr.).
Lad os gå tilbage til nummer 12, som vi kan udtrykke på forskellige måder. Lad os prøve nogle:
12 = 4 x 3 = 2 x 6 = 12 x 1 = 2to x 3 = 3 x 2to = 3 x 2 x 2 = 2 x 2 x 3 = 2 x 3 x 2
De former, der er fremhævet med fed skrift, er produkter med primtal, og det eneste der ændrer sig er rækkefølgen af faktorer, som vi ved ikke ændrer produktet. De andre former, selvom de er gyldige til at udtrykke 12, består ikke udelukkende af primtal.
Hvis vi ønsker at nedbryde et sammensat tal i dets primære faktorer, skal vi dele det mellem primtal på en sådan måde, at divisionen er nøjagtig, dvs. at resten er 0.
Denne procedure kaldes primær faktorisering eller kanonisk nedbrydning. Primære faktorer kan hæves til positive eksponenter.
Vi vil nedbryde tallet 570 og bemærke, at det er jævnt og derfor deleligt med 2, hvilket er et primtal.
Vi bruger en skråstreg for at adskille nummeret til venstre fra skillelinjerne til højre. De respektive kvotienter placeres under nummeret, når de opnås. Nedbrydningen er fuldført, når den sidste figur i venstre kolonne er 1:
570 │2
285 │
Når vi deler med 2, er kvotienten 285, som kan deles med 5, et andet primtal, der slutter med 5.
570 │2
285 5
57 │
57 kan deles med 3, også et primtal, da summen af dets cifre 5 + 7 = 12 er et multiplum af 3.
570 │2
285 5
57 3
19 │
Endelig får vi 19, hvilket er et primtal, hvis skillevægge er 19 og 1:
570 │2
285 5
57 3
19-19
1 │
Ved at opnå 1 kan vi allerede udtrykke 570 på denne måde:
570 = 2 x 5 x 3 x 19
Og vi ser, at det faktisk er produktet af 4 primtal.
I dette eksempel starter vi med at dividere med 2, men de samme faktorer (i en anden rækkefølge) ville være opnået, hvis vi startede med at dividere med 5 for eksempel.
For at nedbryde et sammensat tal i dets primære faktorer er det nødvendigt at opdele det nøjagtigt. Kriterierne for delbarhed mellem primtal er regler, der gør det muligt at vide, hvornår et tal kan deles af en anden nøjagtigt uden at skulle prøve eller bevise.
Alle lige tal, dem der slutter på 0 eller et lige antal, kan deles med 2.
Hvis summen af cifrene i et tal er et multiplum af 3, så kan tallet også deles med 3.
Tal, der slutter med 0 eller 5, kan deles med 5.
Et tal kan deles med 7, hvis den sidste værdi adskilles, multipliceres med 2 og trækker det resterende tal, den resulterende værdi er et multiplum af 7.
Denne regel virker lidt mere kompliceret end de foregående, men i virkeligheden er den ikke så meget, så lad os se på et eksempel: vil 98 være delelig med 7?
Lad os følge instruktionerne: Vi adskiller den sidste figur, som er 8, vi ganger den med 2, hvilket giver 16. Det antal, der er tilbage, når vi adskiller 8, er 9. Vi trækker 16 - 9 = 7. Og da 7 er et multiplum af sig selv , 98 kan deles mellem 7.
Hvis summen af tallene i lige position (2, 4, 6 ...) trækkes fra summen af figurerne i ulige position (1, 3, 5, 7 ...) og 0 eller et multiplum af 11 opnås, opnås tallet kan deles med 11.
De første multipla af 11 kan let identificeres: de er 11, 22, 33, 44 ... 99. Men pas på, 111 er ikke, i stedet for 110 er.
Lad os som et eksempel se, om 143 er et multiplum af 11.
Dette tal har 3 cifre, det eneste lige ciffer er 4 (det andet), de to ulige cifre er 1 og 3 (første og tredje), og deres sum er 4.
Begge summer trækkes fra: 4 - 4 = 0, og da 0 opnås, viser det sig, at 143 er et multiplum af 11.
Nummeret uden cifret skal trækkes fra 9 gange cifret. Hvis optællingen returnerer 0 eller et multiplum af 13, er tallet et multiplum af 13.
Som et eksempel vil vi verificere, at 156 er et multiplum af 13. Tallene på 6 er 6, og tallet, der forbliver uden det, er 15. Vi multiplicerer 6 x 9 = 54, og nu trækker vi 54 - 15 = 39.
Men 39 er 3 x 13, så 56 er et multiplum af 13.
To eller flere prime- eller sammensatte tal kan være prime eller co-prime. Dette betyder, at den eneste fælles skiller, de har, er 1.
Der er to vigtige egenskaber, du skal huske, når det kommer til coprimes:
-To, tre og flere på hinanden følgende tal er altid primære for hinanden.
-Det samme kan siges for to, tre eller flere ulige numre i træk.
For eksempel er 15, 16 og 17 primtal for hinanden, og det samme er 15, 17 og 19.
Et primtal har to skillevægge, det samme tal og 1. Og hvor mange skillevægge har et sammensat tal? Disse kan være fætre eller forbindelser.
Lad N være et sammensat tal udtrykt i form af dets kanoniske nedbrydning som følger:
N = an . bm. cs... rk
Hvor a, b, c ... r er de primære faktorer og n, m, p ... k de respektive eksponenter. Antallet af delere C, som N har, er givet ved:
C = (n +1) (m + 1) (p +1) ... (k + 1)
Med C = hoveddelere + sammensatte delere + 1
For eksempel 570, som udtrykkes således:
570 = 2 x 5 x 3 x 19
Alle primære faktorer hæves til 1, derfor har 570:
C = (1 + 1) (1 + 1) (1+ 1) (1 +1) = 16 skillevægge
Af disse 10 skillevægge kender vi allerede: 1, 2, 3, 5, 19 og 570. Der mangler yderligere 10 skillevægge, som er sammensatte tal: 6, 10, 15, 30, 38, 57, 95, 114, 190 og 285. De findes ved at observere nedbrydningen i primære faktorer og multiplicere kombinationer af disse faktorer sammen..
Nedbryd følgende tal i hovedfaktorer:
a) 98
b) 143
c) 540
d) 3705
98 │2
49 │7
7 │7
1 │
98 = 2 x 7 x 7
143 11
13-13
1 │
143 = 11 x 13
540 │5
108 │2
54 │2
27 │3
9 │3
3 │3
1 │
540 = 5 x 2 x 2 x 3 x 3 x 3 = 5 x 2to x 33
3705 5
741 │3
247 13
19-19
1 │
3705 = 5 x 3 x 13 x 19
Find ud af, om følgende tal er primære for hinanden:
6, 14, 9
-Delerne på 6 er: 1, 2, 3, 6
-Hvad angår de 14, er den delelig med: 1, 2, 7, 14
-Endelig har 9 som skillevægge: 1, 3, 9
Den eneste skiller, de har til fælles, er 1, derfor er de primære for hinanden.
Endnu ingen kommentarer