Det lineære bølger er dem, hvor superpositionsprincippet er anvendeligt, det vil sige dem, hvor bølgeformen og dens rumtidsudvikling kan opnås som summen af grundlæggende løsninger, for eksempel af en harmonisk type. Ikke alle bølger overholder superpositionsprincippet, dem, der ikke overholder det, kaldes ikke-lineære bølger.
Navnet "lineær" kommer fra det faktum, at lineære bølger altid tilfredsstiller en differentialligning i partielle derivater, hvor alle de termer, der involverer den afhængige variabel eller dens derivater, hæves til den første styrke.
På den anden side tilfredsstiller ikke-lineære bølger bølgeligning, der har kvadratiske termer eller højere grader i den afhængige variabel eller i dens derivater.
Lineære bølger forveksles undertiden med længdebølger, som er dem, hvor vibrationen opstår i samme formeringsretning som lydbølger.
Men langsgående bølger såvel som tværgående bølger kan igen være lineære eller ikke-lineære afhængigt af blandt andre faktorer amplituden af den oprindelige forstyrrelse og det medium, hvori de formerer sig..
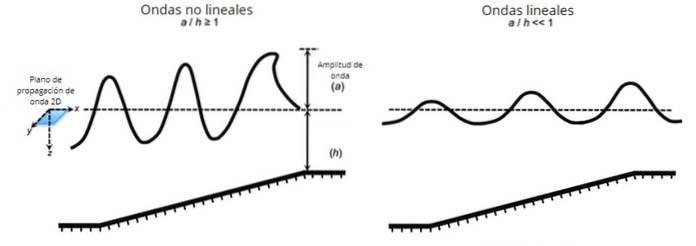
Det sker generelt, at når den oprindelige forstyrrelse er af lille amplitude, er ligningen, der beskriver bølgens udbredelse, lineær eller kan lineæriseres ved visse tilnærmelser, skønt dette ikke altid er tilfældet..
Artikelindeks
I et lineært medium kan en bølgeform begrænset i rum og tid repræsenteres af summen af bølgefunktioner af sinus- eller cosinustypen af forskellige frekvenser og bølgelængder ved hjælp af Fourier-serier.
Lineære bølger har altid associeret en differentialligning af den lineære type, hvis opløsning repræsenterer forudsigelsen af, hvad forstyrrelsen vil være i senere øjeblikke af en indledende forstyrrelse lokaliseret i det første øjeblik.
Den klassiske lineære bølgeligning i en enkelt rumlig dimension, hvis løsninger er lineære bølger er:
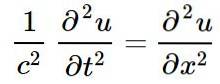
I ovenstående ligning eller repræsenterer forstyrrelsen af en bestemt fysisk størrelse på positionen x og i øjeblikket t, nemlig eller er en funktion af x Y t:
u = u (x, t)
For eksempel, hvis det er en lydbølge i luften, eller kan repræsentere variationen i trykket i forhold til dets værdi uden at forstyrre.
I tilfælde af en elektromagnetisk bølge repræsenterer u det elektriske felt eller magnetfeltet, der oscillerer vinkelret på udbredelsesretningen.
I tilfælde af et stramt reb, eller repræsenterer den tværgående forskydning i forhold til rebets ligevægt, som vist i følgende figur:
Hvis der er to eller flere løsninger af den lineære differentialligning, så vil hver opløsning ganget med en konstant være en løsning, og det samme vil summen af dem.
I modsætning til ikke-lineære ligninger tillader lineære bølge ligninger harmoniske løsninger af typen:
eller1= A⋅sen (k⋅x - ω⋅t) Y ellerto= A⋅sen (k⋅x + ω⋅t)
Dette kan verificeres ved simpel substitution i den lineære bølgeligning.
Den første løsning repræsenterer en vandrende bølge, der bevæger sig til højre, mens den anden løsning til venstre hurtigt c = ω / k.
Harmoniske løsninger er karakteristiske for lineære bølgeligninger.
På den anden side er den lineære kombination af to harmoniske løsninger også en løsning af den lineære bølgeligning, for eksempel:
u = A1 cos (k1⋅x - ω1⋅t) + Ato sen (kto⋅x - ωto⋅t) er løsning.
Det mest relevante kendetegn ved lineære bølger er, at enhver bølgeform, uanset hvor kompleks, kan opnås gennem en summering af enkle harmoniske bølger i sinus og cosinus:
u (x, t) = A0 + ∑n TILn cos (kn⋅x - ωn⋅t) + ∑m Bm sen (km⋅x - ωm⋅t).
I den klassiske lineære bølgeligning, c repræsenterer impulsens forplantningshastighed.
I tilfælde hvor c er en konstant værdi, for eksempel elektromagnetiske bølger i vakuum, derefter en puls i det første øjeblik t = 0 Form f (x) spredes i henhold til:
u (x, t) = f (x - c⋅t)
Uden at lide nogen forvrængning. Når dette sker, siges mediet at være ikke-dispersivt..
I dispersive medier kan udbredelseshastigheden c imidlertid afhænge af bølgelængden λ, det vil sige: c = c (λ).
Elektromagnetiske bølger er spredte, når de rejser gennem et materialemedium. Også vandets overfladebølger bevæger sig med forskellige hastigheder afhængigt af vanddybden.
Den hastighed, hvormed en harmonisk bølge af typen A⋅sen (k⋅x - ω⋅t) det er ω / k = c y kaldes fasehastigheden. Hvis mediet er spredt, så c er en funktion af bølgetallet k: c = c (k), hvor k er relateret til bølgelængde ved k = 2π / λ.
Forholdet mellem frekvens og bølgelængde kaldes dispersionsforhold, end udtrykt i form af vinkelfrekvensen ω og bølgenummeret k det er: ω = c (k) ⋅k.
Nogle karakteristiske spredningsforhold for lineære bølger er som følger:
I havbølger, hvor bølgelængden (afstanden mellem toppen) er meget større end dybden H, men da dens amplitude er meget mindre end dybden, er dispersionsforholdet:
ω = √ (gH) ⋅k
Derfra konkluderes det, at de formerer sig med konstant hastighed √ (gH) (ikke-dispersivt medium).
Men bølger i meget dybe farvande er spredte, da dispergeringsforholdet er:
ω = √ (g / k) ⋅k
Dette betyder, at fasehastigheden ω / k er variabel og afhænger af bølgetallet og derfor af bølgelængden.
Hvis to harmoniske lineære bølger overlapper hinanden, men bevæger sig frem ved forskellige hastigheder, svarer gruppehastigheden (det vil sige af bølgepakken) ikke med fasehastigheden.
Gruppens hastighed vg er defineret som derivatet af frekvensen i forhold til bølgetallet i dispersionsrelationen: vg = ω '(k).
Følgende figur viser superpositionen eller summen af to harmoniske bølger eller1= A⋅sen (k1⋅x - ω1⋅t) Y ellerto= A⋅sen (kto⋅x - ωto⋅t) rejser med forskellige hastigheder v1= ω1/ k1 Y vto= ωto/ kto. Bemærk, hvordan gruppehastigheden er forskellig fra fasehastigheden, i dette tilfælde er gruppehastigheden ∆ω / ∆k.
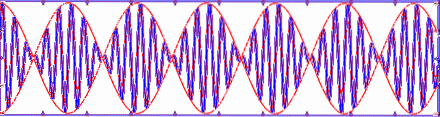
Afhængigt af dispersionsforholdet kan det endda ske, at fasehastigheden og gruppehastigheden i lineære bølger har modsatte retninger..
Elektromagnetiske bølger er lineære bølger. Dens bølgeligning er afledt af ligningerne af elektromagnetisme (Maxwells ligninger), som også er lineære.
Det er ligningen, der beskriver dynamikken i partiklerne på en atomskala, hvor bølgeegenskaberne er relevante, for eksempel tilfældet med elektroner i atomet.
Så "elektronbølgen" eller bølgefunktionen, som den også kaldes, er en lineær bølge.
Lineære bølger er også dem, hvor amplituden er meget mindre end bølgelængden og bølgelængden meget større end dybden. Bølger på dybt vand følger den lineære teori (kendt som Airy wave theory).
Imidlertid er bølgen, der nærmer sig kysten og danner den karakteristiske krøllekam (og som surfere elsker), en ikke-lineær bølge..
Da lyd er en lille forstyrrelse af atmosfærisk tryk, betragtes det som en lineær bølge. Imidlertid er chokbølgen fra en eksplosion eller bølgefronten fra et supersonisk fly typiske eksempler på en ikke-lineær bølge..
Bølgerne, der udbreder sig gennem et stramt reb, er lineære, så længe den oprindelige pulsering er af lille amplitude, dvs. rebets elastiske grænse overskrides ikke..
Lineære bølger i strengene reflekteres ved deres ender og overlapper hinanden, hvilket giver anledning til stående bølger eller vibrationsfunktioner, der giver de harmoniske og subharmoniske toner karakteristiske for strygeinstrumenter..
Endnu ingen kommentarer