
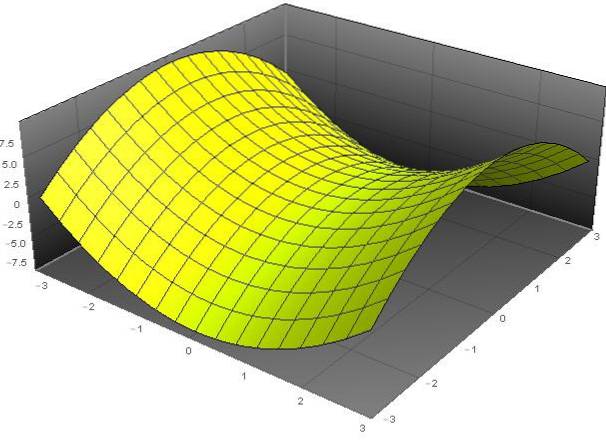
Hyperbolsk paraboloid definition, egenskaber og eksempler

EN hyperbolsk paraboloid er en overflade, hvis generelle ligning i kartesiske koordinater (x, y, z) opfylder følgende ligning:
(til)to - (og / b)to - z = 0.
Navnet "paraboloid" stammer fra det faktum, at variablen z afhænger af kvadraterne for variablerne x og y. Mens adjektivet "hyperbolsk" skyldes det faktum, at ved faste værdier af z har vi ligningen af en hyperbol. Formen på denne overflade svarer til en hestesadel.
Artikelindeks
- 1 Beskrivelse af det hyperbolske paraboloid
- 2 Egenskaber ved hyperbolsk paraboloid
- 3 Arbejdede eksempler
- 3.1 - Eksempel 1
- 3.2 - Eksempel 2
- 3.3 - Eksempel 3
- 4 Det hyperbolske paraboloid i arkitekturen
- 5 Referencer
Beskrivelse af det hyperbolske paraboloid
For at forstå arten af det hyperbolske paraboloid foretages følgende analyse:
1.- Vi vil tage det særlige tilfælde a = 1, b = 1, det vil sige den cartesiske ligning af paraboloid forbliver som z = xto - Yto.
2.- Planer parallelt med ZX-planet betragtes, det vil sige y = ctte.
3.- Med y = ctte forbliver det z = xto - C, som repræsenterer paraboler med forgreninger opad og toppunkt under XY-planet.
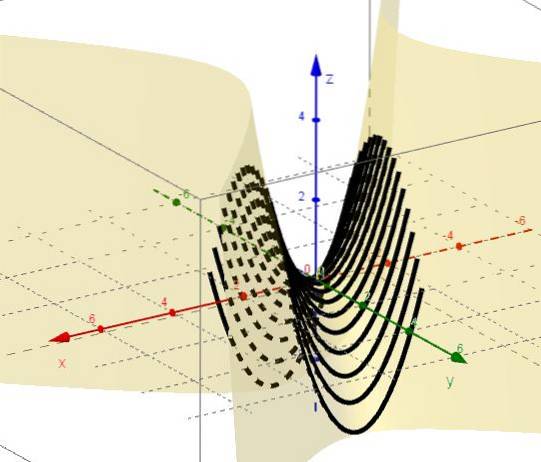
4.- Med x = ctte forbliver det z = C - yto, som repræsenterer paraboler med grene nedad og toppunktet over XY-planet.
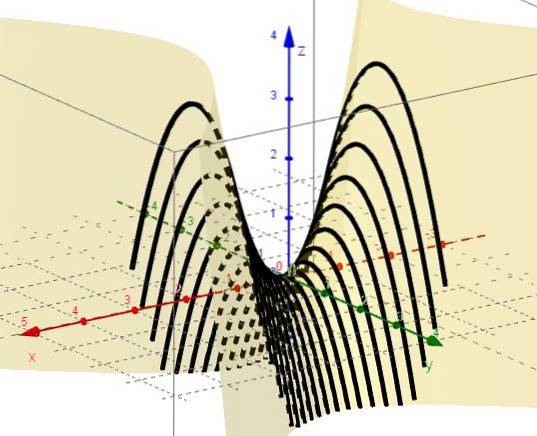
5.- Med z = ctte forbliver det C = xto - Yto, som repræsenterer hyperboler i planer parallelt med XY-planet. Når C = 0 er der to linjer (ved + 45º og -45 ° i forhold til X-aksen), der skærer hinanden ved oprindelsen på XY-planet.
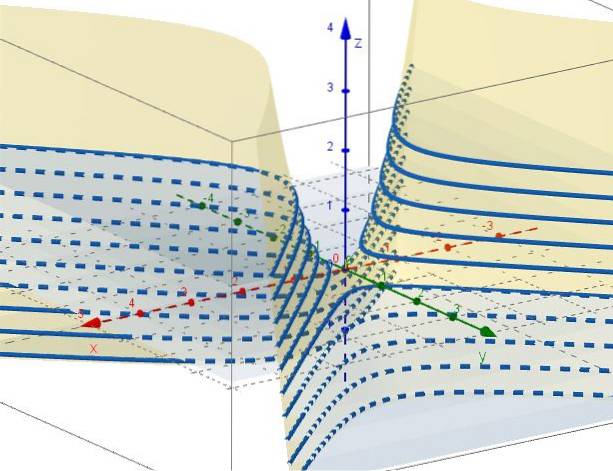
Egenskaber ved det hyperbolske paraboloid
1.- Fire forskellige punkter i det tredimensionelle rum definerer en og kun en hyperbolsk paraboloid.
2.- Den hyperbolske paraboloid er en dobbelt styret overflade. Dette betyder, at til trods for at være en buet overflade, passerer to forskellige linjer gennem hvert punkt i en hyperbolsk paraboloid, der helt hører til den hyperbolske paraboloid. Den anden overflade, der ikke er et plan og er dobbelt styret, er revolution af hyperboloid.
Det er netop den anden egenskab ved det hyperbolske paraboloid, der har tilladt dets store anvendelse i arkitektur, da overfladen kan genereres fra bjælker eller lige reb..
Den anden egenskab ved det hyperbolske paraboloid tillader en alternativ definition af det: er overfladen, der kan genereres af en bevægende lige linje parallelt med et fast plan og skærer to faste linjer, der fungerer som en guide. Følgende figur præciserer denne alternative definition af hyperbolsk paraboloid:
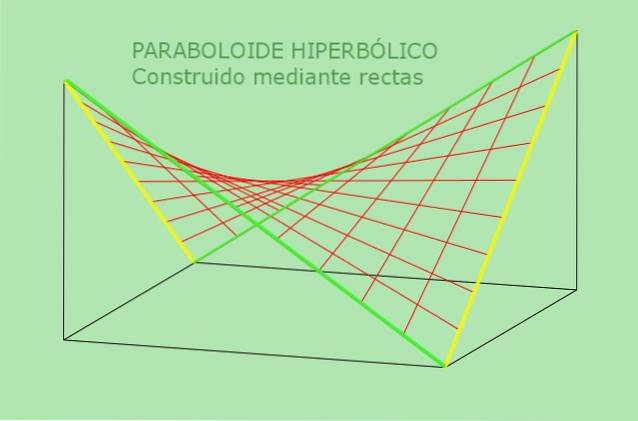
Arbejdede eksempler
- Eksempel 1
Vis, at ligningen: z = xy, svarer til en hyperbolsk paraboloid.
Opløsning
En transformation vil blive anvendt på variablerne x og y svarende til en rotation af de kartesiske akser i forhold til Z-aksen på + 45º. De gamle x- og y-koordinater omdannes til de nye x 'og y' i henhold til følgende forhold:
x = x '- y'
y = x '+ y'
mens z-koordinaten forbliver den samme, det vil sige z = z '.
Ved at erstatte ligningen z = x, og vi har:
z '= (x' - y ') (x' + y ')
Ved at anvende det bemærkelsesværdige produkt af forskellen med summen lig med forskellen i firkanter, har vi:
z '= x'to - Y 'to
hvilket klart svarer til den oprindeligt givne definition af hyperbolsk paraboloid.
Opfangningen af flyene parallelt med XY-aksen med den hyperbolske paraboloid z = x og bestemme ligesidede hyperboler, der har asymptoter på planene x = 0 og y = 0.
- Eksempel 2
Bestem parametrene til Y b af det hyperbolske paraboloid, der passerer gennem punkterne A (0, 0, 0); B (1, 1, 5/9); C (-2, 1, 32/9) og D (2, -1, 32/9).
Opløsning
Ifølge dens egenskaber bestemmer fire punkter i det tredimensionelle rum en enkelt hyperbolsk paraboloid. Den generelle ligning er:
z = (x / a)to - (og / b)to
Vi erstatter de givne værdier:
For punkt A har vi 0 = (0 / a)to - (0 / b)to, ligning, der er tilfreds uanset parametrernes værdier a og b.
Ved at erstatte punkt B opnår vi:
5/9 = 1 / ato - 1 Bto
Mens det for punkt C forbliver:
32/9 = 4 / ato - 1 Bto
Endelig opnår vi for punkt D:
32/9 = 4 / ato - 1 Bto
Hvilket er identisk med den tidligere ligning. I sidste ende skal ligningssystemet løses:
5/9 = 1 / ato - 1 Bto
32/9 = 4 / ato - 1 Bto
At trække den anden ligning fra den første giver:
27/9 = 3 / ato hvilket indebærer, at ento = 1.
Tilsvarende trækkes den anden ligning fra firdoblingen af den første og opnår:
(32-20) / 9 = 4 / ato - 4 / ato -1 Bto + 4 / bto
Hvilket er forenklet som:
12/9 = 3 / bto ⇒ bto = 9/4.
Kort sagt har den hyperbolske paraboloid, der passerer gennem de givne punkter A, B, C og D, en kartesisk ligning givet af:
z = xto - (4/9) ogto
- Eksempel 3
I henhold til egenskaberne ved det hyperbolske paraboloid passerer to linjer gennem hvert punkt, der er helt indeholdt i det. For tilfældet z = x ^ 2 - y ^ 2 find ligningen af de to linjer, der passerer gennem punktet P (0, 1, -1), der klart hører til det hyperbolske paraboloid, således at alle punkterne i disse linjer også hører til til det samme.
Opløsning
Ved hjælp af det bemærkelsesværdige produkt af forskellen i firkanter kan ligningen for det hyperbolske paraboloid skrives således:
(x + y) (x - y) = c z (1 / c)
Hvor c er en ikke-nul konstant.
Ligningen x + y = c z, og ligningen x - y = 1 / c svarer til to plan med normale vektorer n=<1,1,-c> Y m=<1,-1,0>. Vektorproduktet m x n =<-c, -c, -2> giver os retningen af skæringslinjen mellem de to planer. Derefter har en af linjerne, der passerer gennem punktet P og tilhører den hyperbolske paraboloid, en parametrisk ligning:
For at bestemme c erstatter vi punktet P i ligningen x + y = c z og opnår:
c = -1
På en lignende måde, men i betragtning af ligningerne (x - y = k z) og (x + y = 1 / k) har vi den parametriske ligning af linjen:
Sammenfattende er de to linjer:
De er fuldstændigt indeholdt i den hyperbolske paraboloid z = xto - Yto passerer gennem punktet (0, 1, -1).
Antag som en kontrol, at t = 1, som giver os punktet (1,2, -3) på den første linje. Du skal kontrollere, om det også er på paraboloid z = xto - Yto:
-3 = 1to - toto = 1-4 = -3
Hvilket bekræfter, at det faktisk hører til overfladen af det hyperbolske paraboloid.
Den hyperbolske paraboloid i arkitekturen

Den hyperbolske paraboloid er blevet brugt i arkitekturen af de store avantgarde arkitekter, blandt hvilke navnene på den spanske arkitekt Antoni Gaudí (1852-1926) og især den også spanske Félix Candela (1910-1997) skiller sig ud..
Nedenfor er nogle værker baseret på den hyperbolske paraboloid:
-Kapel i byen Cuernavaca (Mexico) arbejder af arkitekten Félix Candela.
-The Oceanographic of Valencia (Spanien), også af Félix Candela.
Referencer
- Encyklopædi for matematik. Reguleret overflade. Gendannet fra: encyclopediaofmath.org
- Llera Rubén. Hyperbolisk paraboloid. Gendannet fra: rubenllera.wordpress.com
- Weisstein, Eric W. "Hyperbolsk paraboloid." Fra MathWorld-A Wolfram Web Resource. Gendannet fra: mathworld.wolfram.com
- Wikipedia. Paraboloid. Gendannet fra: en.wikipedia.com
- Wikipedia. Paraboloid. Gendannet fra: es.wikipedia.com
- Wikipedia. Reguleret overflade. Gendannet fra: en.wikipedia.com


Endnu ingen kommentarer