Det Pascals princip, eller Pascals lov, fastslår, at en ændring i trykket af en væske, der er begrænset i et af dens punkter, transmitteres uden ændring til alle andre punkter i væsken.
Dette princip blev opdaget af den franske videnskabsmand Blaise Pascal (1623 - 1662). På grund af vigtigheden af de bidrag, Pascal har ydet til videnskaben, er presseenheden i det internationale system blevet udnævnt til hans ære..
Da tryk defineres som forholdet mellem kraften vinkelret på en overflade og dens areal, er 1 Pascal (Pa) lig med 1 newton / mto.
Artikelindeks
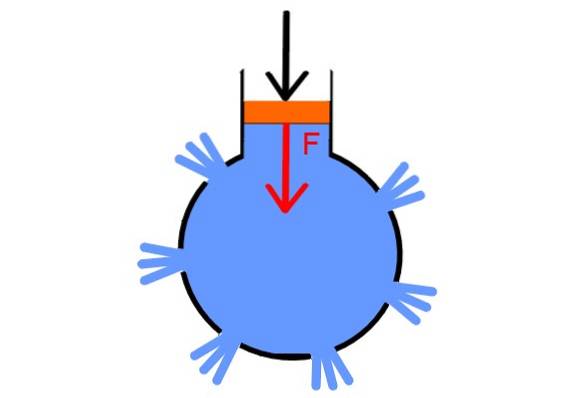
For at teste sit princip udtænkte Pascal et ret kraftigt bevis. Han tog en hul kugle og borede flere steder, satte propper i alle hullerne undtagen en, hvorigennem han fyldte den med vand. I dette placerede han en sprøjte udstyret med et stempel.
Ved tilstrækkeligt at øge trykket i stemplet frigøres propperne på samme tid, fordi trykket overføres ens til alle punkter i væsken og i alle retninger, hvilket viser Pascals lov.
Blaise Pascal havde et kort liv præget af sygdom. Hans utrolige omfang førte ham til at undersøge forskellige aspekter af naturen og filosofien. Hans bidrag var ikke begrænset til at studere væskers opførsel, Pascal var også en pioner inden for computing.
Og det er, at Pascal i en alder af 19 oprettede en mekanisk regnemaskine, som hans far kunne bruge i sit arbejde i det franske skattesystem: pascaline.
Sammen med sin ven og kollega den store matematiker Pierre de Fermat formede de også teorien om sandsynligheder, der er uundværlig inden for fysik og statistik. Pascal døde i Paris i en alder af 39 år.
Følgende eksperiment er ret simpelt: et U-rør er fyldt med vand, og propper placeres i hver ende, der kan glide jævnt og let, som stempler. Der trykkes mod venstre stempel, synker det lidt, og det observeres, at det til højre stiger, skubbet af væsken (figur nedenfor).
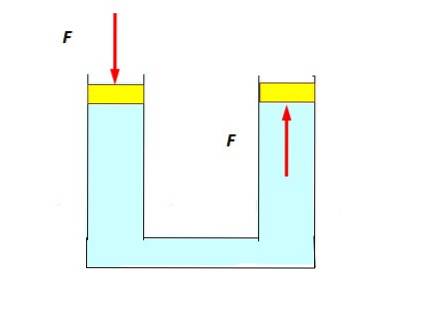
Dette sker, fordi trykket transmitteres uden fald til alle væskepunkter, inklusive dem, der er i kontakt med stemplet til højre..
Væsker som vand eller olie er ikke-komprimerbare, men samtidig har molekylerne tilstrækkelig bevægelsesfrihed, hvilket gør det muligt for trykket at blive fordelt over det rigtige stempel..
Takket være dette modtager det højre stempel en kraft, der er nøjagtig ens i størrelse og retning til den, der påføres til venstre, men i den modsatte retning..
Trykket i en statisk væske er uafhængig af beholderens form. Det vil snart blive vist, at trykket varierer lineært med dybden, og Pascals princip er en konsekvens af dette..
En ændring i tryk på ethvert tidspunkt får trykket på et andet punkt til at ændre sig med samme mængde. Ellers ville der være et ekstra tryk, der ville få væsken til at strømme.
En væske i hvile udøver en kraft på beholdervæggene, der indeholder den, og også på overfladen af ethvert objekt nedsænket i den. I Pascals sprøjteeksperiment ses det, at vandstrålerne kommer ud vinkelret til sfæren.
Væskerne fordeler kraften vinkelret på overfladen, som den virker på, det er derfor det er praktisk at introducere begrebet gennemsnitstryk Pm som den lodrette kraft, der udøves F⊥ Efter område TIL, hvis SI-enhed er pascal:
Pm = F⊥ / TIL
Trykket øges med dybden. Det kan ses ved at isolere en lille del af væske i statisk ligevægt og anvende Newtons anden lov:
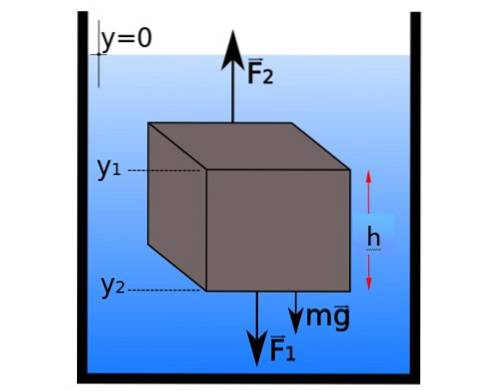
De vandrette kræfter annullerer parvis, men i lodret retning er kræfterne grupperet således:
∑FY = Fto - F1 - mg = 0 → Fto - F1 = mg
Udtrykker masse udtrykt i densitet ρ = masse / volumen:
Pto.A- P1.A = ρ x volumen x g
Volumenet af væskedelen er produktet A x h:
A. (sto - P1) = ρ x A x h x g
ΔP = ρ.g.h Grundlæggende sætning af hydrostatik
Pascals princip er blevet brugt til at opbygge adskillige enheder, der multiplicerer kraft og letter opgaver såsom løft af vægte, stempling på metal eller presning af genstande. Blandt dem er:
-Den hydrauliske presse
-Bilens bremsesystem
-Mekaniske skovle og mekaniske arme
-Den hydrauliske donkraft
-Kraner og elevatorer
Lad os derefter se, hvordan Pascals princip forvandler små kræfter til store kræfter til at udføre alle disse job. Den hydrauliske presse er det mest karakteristiske eksempel og analyseres nedenfor.
For at bygge en hydraulisk presse tages den samme enhed som figuren ovenfor, det vil sige en U-formet beholder, som vi allerede ved, at den samme kraft overføres fra det ene stempel til det andet. Forskellen vil være størrelsen på stemplerne, og det er det, der får enheden til at fungere.
Følgende figur viser Pascals princip i aktion. Trykket er det samme på alle punkter i væsken, både i det lille og store stempel:
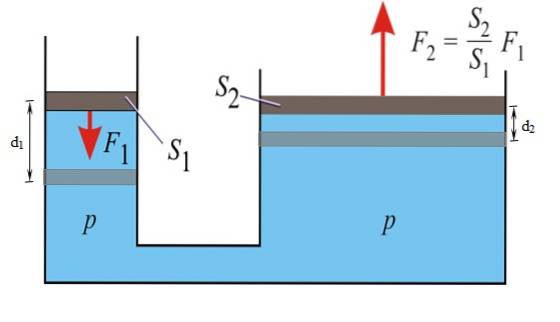
p = F1 / S1 = Fto / Sto
Størrelsen af kraften, der transmitteres til det store stempel, er:
Fto = (Sto / S1). F1
Kan lideto > S1, resulterer i Fto > F1, derfor er outputkraften ganget med den faktor, der er givet af kvotienten mellem områderne.
Dette afsnit præsenterer applikationseksempler.
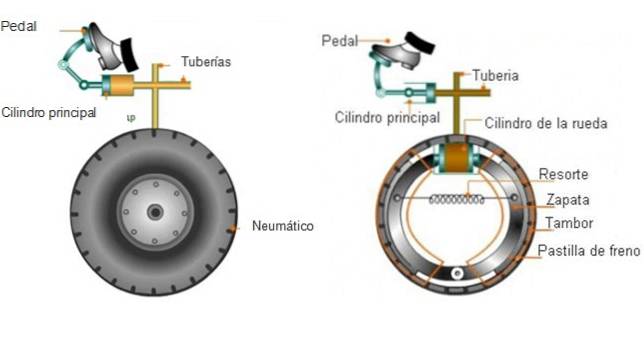
Bilbremser gør brug af Pascals princip gennem en hydraulisk væske, der fylder rør, der er forbundet med hjulene. Når han skal stoppe, anvender føreren en kraft ved at trykke bremsepedalen ned og skabe væsketryk.
På den anden side presser tryk bremseklodserne mod tromlen eller bremseskiverne, der roterer sammen med hjulene (ikke dækkene). Den resulterende friktion får disken til at stoppe og bremser også hjulene.
I den hydrauliske presse i nedenstående figur skal input-arbejdet være lig med output-arbejdet, så længe der ikke tages højde for friktion..
Indgangskraft F1 får stemplet til at køre en afstand d1 går ned, mens outputkraften Fto tillader en rundvisning dto af det stigende stempel. Hvis det mekaniske arbejde udført af begge kræfter er det samme:
F1.d1 = Fto. dto
Den mekaniske fordel M er kvotienten mellem størrelsen af inputkraften og outputkraften:
M = Fto/ F1 = d1/ dto
Og som vist i det foregående afsnit, kan det også udtrykkes som kvotienten mellem områderne:
Fto/ F1 = Sto / S1
Det ser ud til, at der kan arbejdes gratis, men i virkeligheden skabes der ikke energi med denne enhed, da den mekaniske fordel opnås på bekostning af forskydningen af det lille stempel d1.
For at optimere ydelsen tilføjes et ventilsystem til enheden på en sådan måde, at udgangsstemplet stiger takket være korte impulser på indløbsstemplet..
På denne måde pumper operatøren af et hydraulisk garagestykke flere gange for gradvist at løfte et køretøj..
I den hydrauliske presse i figur 5 er stempelarealerne 0,5 kvadrat inches (lille stempel) og 25 kvadrat inches (stort stempel). Finde:
a) Den mekaniske fordel ved denne presse.
b) Den krævede kraft til at løfte en belastning på 1 ton.
c) Den afstand, inputkraften skal virke for at løfte belastningen med 1 tomme.
Udtryk alle resultater i enheder af det britiske system og SI International System.
a) Den mekaniske fordel er:
M = Fto/ F1 = Sto/ S1 = 25 tommerto / 0,5 tommerto = 50
b) 1 ton er lig med 2000 lb-kraft. Den krævede kraft er F1:
F1 = Fto / M = 2000 lb-kraft / 50 = 40 lb-kraft
For at udtrykke resultatet i det internationale system kræves følgende konverteringsfaktor:
1 lb-kraft = 4.448 N
Derfor er størrelsen af F1 177,92 N.
c) M = d1/ d2 → d1 = M.dto = 50 x 1 in = 50 in
Den nødvendige konverteringsfaktor er: 1 in = 2,54 cm
d1 = 127 cm = 1,27 m
Endnu ingen kommentarer