
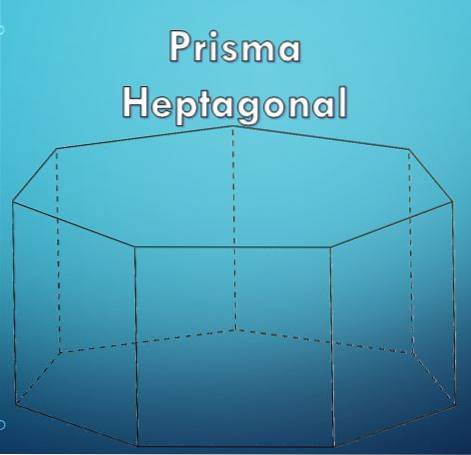
Heptagonal prismeegenskaber, volumen, areal
EN heptagonalt prisme Det er en geometrisk figur, der, som navnet antyder, involverer to geometriske definitioner, der er: prisme og heptagon. Et "prisme" er en geometrisk figur begrænset af to baser, der er ens og parallelle polygoner, og deres laterale flader er parallelogrammer..
En "heptagon" er en polygon, der består af syv (7) sider. Da en heptagon er en polygon, kan den være regelmæssig eller uregelmæssig.
En polygon siges at være regelmæssig, hvis alle dens sider har samme længde og dens indre vinkler måler den samme, de kaldes også ligesidede polygoner; ellers siges polygonen at være uregelmæssig.

Karakteristika for et heptagonalt prisme
Nedenfor er visse karakteristika, som et heptagonalt prisme har, såsom: dets konstruktion, dens basers egenskaber, arealet med alle dens ansigter og dets volumen..
1- Konstruktion
For at opbygge et heptagonalt prisme er to heptagoner nødvendige, hvilket vil være dens baser og syv parallelogrammer, en til hver side af heptagonen..
Du starter med at tegne en heptagon, så trækkes syv lodrette linjer, af samme længde, der kommer ud fra hver af dens hjørner.
Endelig tegnes en anden heptagon således, at dens hjørner falder sammen med slutningen af linjerne trukket i det foregående trin..
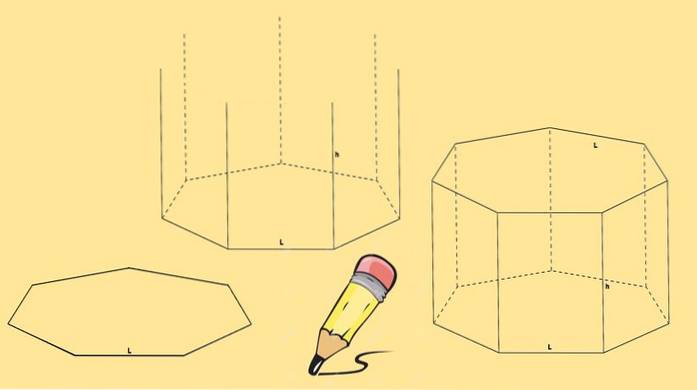
Det heptagonale prisme, der er tegnet ovenfor, kaldes et rigtigt heptagonalt prisme. Men du kan også have et skråt heptagonalt prisme som det i den følgende figur.

2- Egenskaber for dets baser
Da dens baser er heptagoner, tilfredsstiller de, at det diagonale tal er D = nx (n-3) / 2, hvor "n" er antallet af sider af polygonen; i dette tilfælde har vi D = 7 × 4/2 = 14.
Vi kan også se, at summen af de interne vinkler af enhver heptagon (regelmæssig eller uregelmæssig) er lig med 900º. Dette kan bekræftes af følgende billede.
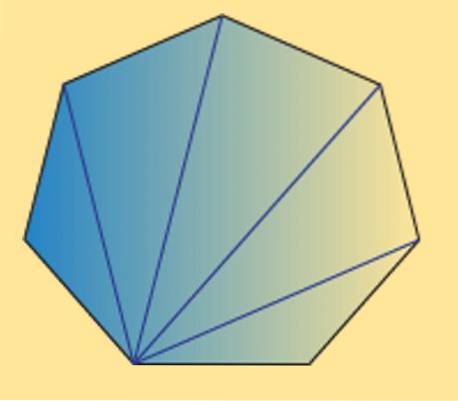
Som det kan ses, er der 5 interne trekanter, og hvis summen af de indre vinkler i en trekant er lig med 180 °, kan det opnås, at det ønskede resultat.
3- Område, der er nødvendigt for at opbygge et heptagonalt prisme
Da dens baser er to heptagoner, og dens sider er syv parallelogrammer, er det område, der er nødvendigt for at opbygge et heptagonalt prisme, lig med 2xH + 7xP, hvor “H” er området for hver heptagon, og “P” er området for hvert parallelogram..
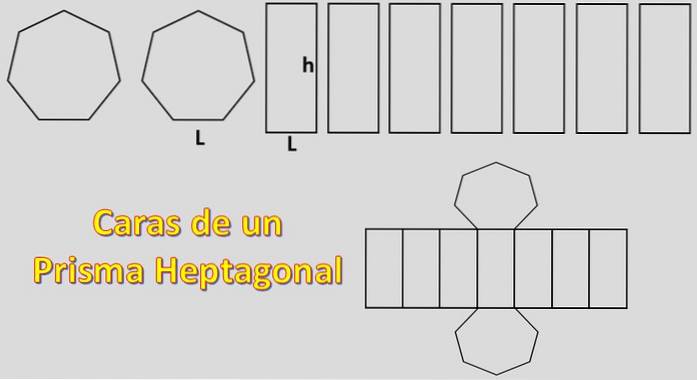
I dette tilfælde beregnes arealet af en almindelig heptagon. Til dette er det vigtigt at kende definitionen af apothem.
Apotemet er en vinkelret linje, der går fra midten af en regelmæssig polygon til midtpunktet på en af dens sider.
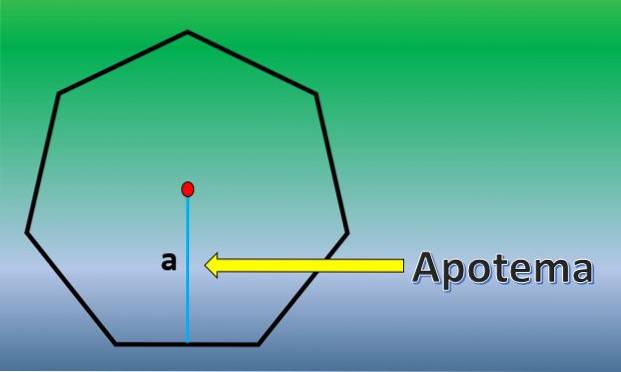
Når apotemet er kendt, er heptagons område H = 7xLxa / 2, hvor "L" er længden af hver side, og "a" er længden af apotemet..
Arealet af et parallelogram er let at beregne, det defineres som P = Lxh, hvor "L" har samme længde som siden af heptagon og "h" er prismaets højde.
Afslutningsvis er mængden af materiale, der er nødvendigt for at opbygge et heptagonalt prisme (med regelmæssige baser) 7xLxa + 7xLxh, det vil sige 7xL (a + h).
4- bind
Når arealet af en base og prismehøjden er kendt, defineres lydstyrken som (areal af basen) x (højde).
I tilfælde af et heptagonalt prisme (med regelmæssig base) er dets volumen V = 7xLxaxh / 2; det kan også skrives som V = Pxaxh / 2, hvor "P" er omkredsen af den almindelige heptagon.
Referencer
- Billstein, R., Libeskind, S., & Lott, J. W. (2013). Matematik: En problemløsningsmetode for lærere i grundskolen. López Mateos Redaktører.
- Fregoso, R. S. og Carrera, S. A. (2005). Matematik 3. Redaktionel Progreso.
- Gallardo, G., og Pilar, P. M. (2005). Matematik 6. Redaktionel Progreso.
- Gutiérrez, C. T. og Cisneros, M. P. (2005). Matematik Kursus 3. Redaktionel Progreso.
- Kinsey, L. og Moore, T. E. (2006). Symmetri, form og rum: En introduktion til matematik gennem geometri (illustreret, genoptrykt red.). Springer Science & Business Media.
- Mitchell, C. (1999). Blændende matematiklinjedesign (Illustreret red.). Scholastic Inc..
- R., M. P. (2005). Jeg trækker 6.. Redaktionel Progreso.



Endnu ingen kommentarer