Det betinget sandsynlighed Det er muligheden for forekomst af en bestemt begivenhed, da en anden forekommer som en tilstand. Disse yderligere oplysninger kan (eller måske ikke) ændre opfattelsen af, at noget vil ske.
For eksempel kan vi spørge os selv: "Hvad er sandsynligheden for, at det regner i dag, i betragtning af at det ikke har regnet i to dage?" Den begivenhed, som vi vil vide sandsynligheden for, er, at det regner i dag, og de yderligere oplysninger, der vil betyde svaret, er at "det har ikke regnet i to dage".
Vær en sandsynligt rum sammensat af Ω (prøveplads), ℬ (tilfældige begivenheder) og P (sandsynligheden for hver begivenhed) plus begivenhederne A og B, der hører til ℬ.
Den betingede sandsynlighed for, at A forekommer, givet at B opstod, der betegnes som P (A│B), er defineret som følger:
P (A│B) = P (A∩B) / P (B) = P (A og B) / P (B)
Hvor: P (A) er sandsynligheden for forekomst af A, P (B) er sandsynligheden for begivenhed B og er forskellig fra 0, og P (A∩B) er sandsynligheden for skæringspunktet mellem A og B, dvs. , sandsynligheden for, at begge begivenheder forekommer (fælles sandsynlighed).
Dette er et udtryk for Bayes 'sætning anvendt på to begivenheder, foreslået i 1763 af den engelske teolog og matematiker Thomas Bayes.
Artikelindeks
-Hver betinget sandsynlighed er mellem 0 og 1:
0 ≤ P (A│B) ≤ 1
-Sandsynligheden for, at begivenhed A forekommer, givet denne begivenhed, er selvfølgelig 1:
P (A│A) = P (A∩A) / P (A) = P (A) / P (A) = 1
-Hvis to begivenheder er eksklusive, dvs. begivenheder, der ikke kan ske samtidigt, er den betingede sandsynlighed for, at en af dem sker, 0, da skæringspunktet er nul:
P (A│B) = P (A∩B) / P (B) = 0 / P (B) = 0
-Hvis B er en delmængde af A, er den betingede sandsynlighed også 1:
P (B│A) = P (A∩B) / P (A) = 1
Vigtig
P (A│B) er generelt ikke lig med P (B│A), derfor skal vi være forsigtige med ikke at udveksle begivenhederne, når vi finder den betingede sandsynlighed.
Mange gange vil du finde den fælles sandsynlighed P (A∩B) snarere end den betingede sandsynlighed. Derefter har vi gennem følgende sætning:
P (A∩B) = P (A og B) = P (A│B). P (B)
Teoremet kan udvides til tre begivenheder A, B og C:
P (A∩B∩C) = P (A og B og C) = P (A) P (B│A) P (C│A∩B)
Og også til forskellige begivenheder, såsom A1, TILto, TIL3 og mere kan det udtrykkes som følger:
P (A1∩ Ato ∩ A3… ∩ An) = P (A.1). P (Ato│A1). P (A3│A1∩ Ato) ... P (An││A1∩ Ato∩… An-1)
Når det er tilfældet med begivenheder, der forekommer i rækkefølge og gennem forskellige faser, er det praktisk at organisere dataene i et diagram eller en tabel. Dette gør det lettere at visualisere mulighederne for at nå den ønskede sandsynlighed..
Eksempler på dette er trædiagram og beredskabstabel. Fra en af dem kan du bygge den anden.
Lad os se på nogle situationer, hvor sandsynligheden for en begivenhed ændres ved forekomsten af en anden:
To typer kager sælges i en sød butik: jordbær og chokolade. Ved at registrere præferencer for 50 klienter af begge køn blev følgende værdier bestemt:
-27 kvinder, hvoraf 11 foretrækker jordbærkage og 16 chokoladekage.
-23 mænd: 15 vælger chokolade og 8 jordbær.
Sandsynligheden for, at en kunde vælger en chokoladekage, kan bestemmes ved at anvende Laplace's regel, ifølge hvilken sandsynligheden for enhver begivenhed er:
P = antal gunstige begivenheder / samlet antal begivenheder
I dette tilfælde foretrækker i alt 31 ud af 50 kunder chokolade, så sandsynligheden ville være P = 31/50 = 0,62. Det vil sige, 62% af kunderne foretrækker chokoladekage.
Men ville det være anderledes, hvis klienten er en kvinde? Dette er et tilfælde af betinget sandsynlighed.
Ved hjælp af en beredskabstabel som denne vises totalerne let:
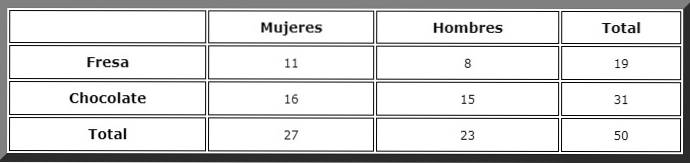
Derefter observeres de gunstige tilfælde, og Laplace's regel anvendes, men først definerer vi begivenhederne:
-B er begivenheden "kvindelig klient".
-A er begivenheden "foretrækker chokoladekage" som kvinde.
Vi går til kolonnen mærket "kvinder", og der ser vi, at det samlede antal er 27.
Derefter søges den gunstige sag i rækken "chokolade". Der er 16 af disse begivenheder, og derfor er sandsynligheden direkte:
P (A│B) = 16/27 = 0,5924
59,24% af de kvindelige kunder foretrækker chokoladekage.
Denne værdi falder sammen, når vi kontrasterer den med den oprindeligt givne definition af betinget sandsynlighed:
P (A│B) = P (A∩B) / P (B)
Vi sørger for at bruge Laplace's regel og værdierne i tabellen:
P (B) = 27/50
P (A og B) = 16/50
Hvor P (A og B) er sandsynligheden for, at kunden foretrækker chokolade og er kvinde. Nu er værdierne erstattet:
P (A│B) = P (A og B) / P (B) = (16/50) / (27/50) = 16/27 = 0,5924.
Og det er bevist, at resultatet er det samme.
I dette eksempel gælder multiplikationsreglen. Antag, at der er bukser i tre størrelser, der vises i en butik: små, mellemstore og store..
I en masse med i alt 24 bukser, hvoraf der er 8 i hver størrelse og alle er blandede, hvad ville sandsynligheden for at udtrække to af dem og at begge var små?
Det er klart, at sandsynligheden for at fjerne en lille bukser ved første forsøg er 8/24 = 1/3. Nu er den anden udtrækning betinget af den første begivenhed, da når man fjerner et par bukser, er der ikke længere 24, men 23. Og hvis en lille bukse fjernes, er der 7 i stedet for 8.
Begivenhed A trækker en lille buks efter at have trukket en til ved første forsøg. Og begivenhed B er den første gang med de små bukser. Derfor:
P (B) = 1/3; P (A│B) = 7/24
Endelig ved hjælp af multiplikationsreglen:
P (A∩B) = (7/24). (1/3) = 7/72 = 0,097
I en undersøgelse af punktlighed på kommercielle flyvninger er følgende data tilgængelige:
-P (B) = 0,83, er sandsynligheden for, at et fly starter til tiden.
-P (A) = 0,81, er sandsynligheden for landing til tiden.
-P (B∩A) = 0,78 er sandsynligheden for, at flyvningen ankommer til tiden og tager fart til tiden.
Det bliver bedt om at beregne:
a) Hvad er sandsynligheden for, at flyet lander til tiden i betragtning af at det startede til tiden?
b) Er den tidligere sandsynlighed den samme som sandsynligheden for, at han forlod til tiden, hvis det lykkedes ham at lande til tiden??
c) Og endelig: hvad er sandsynligheden for, at den ankommer til tiden i betragtning af det ikke kom ud til tiden?
For at besvare spørgsmålet anvendes definitionen af betinget sandsynlighed:
P (A│B) = P (A∩B) / P (B) = P (A og B) / P (B) = 0,78 / 0,83 = 0,9398
I dette tilfælde udveksles begivenhederne i definitionen:
P (B│A) = P (A∩B) / P (A) = P (A og B) / P (A) = 0,78 / 0,81 = 0,9630
Bemærk, at denne sandsynlighed er lidt anderledes end den forrige, som vi tidligere har påpeget.
Sandsynligheden for ikke at rejse til tiden er 1 - P (B) = 1 - 0,83 = 0,17, vi kalder det P (BC), fordi det er den supplerende begivenhed at tage af sted til tiden. Den ønskede betingede sandsynlighed er:
P (A│BC) = P (A∩BC) / P (BC) = P (A og B.C) / P (BC)
På den anden side:
P (A∩BC) = P (landing til tiden) - P (landing til tiden og start til tiden) = 0,81-0,78 = 0,03
I dette tilfælde er den ønskede betingede sandsynlighed:
P (A│BC) = 0,03 / 0,17 = 0,1765
Endnu ingen kommentarer