Det kartografisk konisk projektion Det er kendetegnet ved at projicere punkterne på en sfærisk overflade på overfladen af en kegle, hvis toppunkt er placeret på aksen, der passerer gennem polerne og er tangent eller secant til sfæren. Keglen er en overflade, der kan åbnes i et plan og danner en vinkelsektor uden at deformere de linjer, der er projiceret på den.
Matematikeren Johann Heinrich Lambert (1728 - 1777) var den, der udtænkte denne projektion, og dukkede op for første gang i sin bog Freye Perspektiv (1759), hvor han samlede forskellige teorier og refleksioner over fremskrivninger.
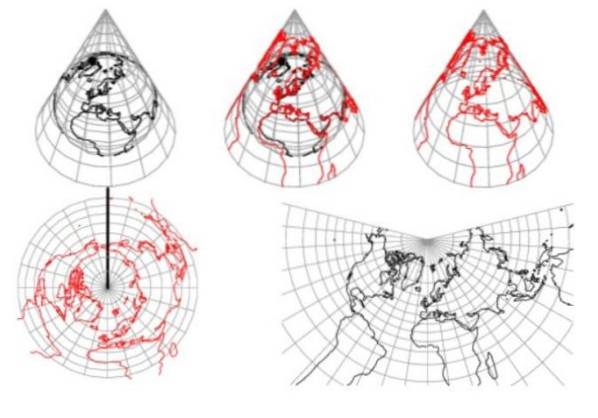
I koniske fremspring på jordoverfladen bliver meridianerne radiale linjer centreret på toppunktet med lige vinkelafstand, og de jordiske paralleller bliver cirkelbuer koncentriske til toppunktet.
Figur 1 viser, at den koniske fremspring ikke tillader at repræsentere begge halvkugler. Derudover bemærkes det tydeligt, at afstandene er forvrænget væk fra parallellerne, der opfanger keglen.
Af disse grunde anvendes denne type projektion til at repræsentere regioner i mellembreddegrad, omfattende fra øst til vest og i mindre nord-sydlig udstrækning. Sådan er det i det kontinentale USA.
Artikelindeks
Jorden kan tilnærmes til en kugle med en radius på 6378 km, i betragtning af at alle land- og vandmasser er på den store kugle. Det handler om at konvertere denne overflade, der dækker et objekt i tre dimensioner, såsom en kugle, til et andet objekt i to dimensioner: et fladt kort. Dette medfører ulejligheden, at den buede overflade er forvrænget, når man ønsker at projicere den på flyet.
Kortfremspring, såsom den koniske fremspring, forsøger at løse dette problem med så lidt tab af nøjagtighed som muligt. Derfor er der flere muligheder for at lave en projektion afhængigt af de egenskaber, du vil fremhæve..
Blandt disse vigtige egenskaber er afstande, overfladeareal, vinkler og mere. Den bedste måde at bevare dem alle på er at repræsentere Jorden i 3D til målestok. Men det er ikke altid praktisk.
At bære en klode overalt er ikke let, da det optager volumen. Du kan heller ikke se hele jordoverfladen på én gang, og det er umuligt at gengive alle detaljerne på en skalamodel..
Vi kan forestille os, at planeten er en appelsin, vi skræller appelsinen og spreder skrælen på bordet og forsøger at rekonstruere billedet af appelsinens overflade. Det er klart, at en masse information går tabt i processen.
Projektionsmulighederne er som følger:
- Projekter på et fly eller
- På en cylinder, der kan udvikles som et rektangulært plan.
- Endelig på en kegle.
Det koniske projektionssystem har den fordel, at det er nøjagtigt i forhold til de paralleller, der er valgt til at opfange projektionskeglen..
Derudover holder det orientering langs meridianerne praktisk talt intakt, selvom det kan fordreje skalaen langs meridianerne noget for breddegrader langt fra standard- eller referenceparalleller. Derfor er det hensigtsmæssigt at repræsentere meget store lande eller kontinenter.
Det er det koniske projektionssystem, der oprindeligt blev brugt af Ptolemaios, en græsk geograf, der boede mellem 100-170 e.Kr. Senere i 1745 blev det forbedret.
Det bruges ofte i atlaserne i regioner med mellemliggende breddegrader. Det er velegnet til at vise områder med et par breddegrader, og som hører til en af ækvatoriale halvkugler.
I denne projektion er afstandene sande langs meridianerne og i de to standardparalleller, det vil sige de paralleller, der er valgt til at opfange med projektionskeglen..
I den ækvidistante koniske fremspring strækker et punkt på sfæren sig radialt indtil dets skæringspunkt med tangent- eller sekantkeglen og tager midten af sfæren som projektionscenteret.
Ulemper
Den største ulempe ved den koniske fremspring er, at den ikke gælder for ækvatoriale regioner.
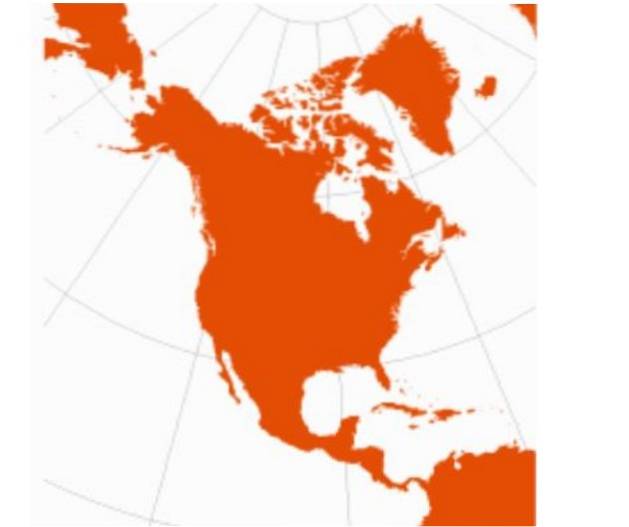
Derudover er den koniske fremspring ikke passende til kortlægning af store regioner, men snarere bestemte områder, såsom Nordamerika..
Brug to standardparalleller og bevar arealet, men ikke skala og form. Denne type konisk fremspring blev introduceret af H. C. Albers i 1805.
Alle områder på kortet er proportionale med dem på Jorden. I begrænsede regioner er retningen ret nøjagtig. Afstande svarer til afstandene fra den sfæriske overflade på standardparallellerne.
I USA bruges dette projektionssystem til kort, der viser grænserne for Unionens stater, for hvilke 29,5 º N og 45,5 º N vælges som standardparalleller, hvilket resulterer i en maksimal skalafejl på 1, 25%.
Kort lavet med denne projektion bevarer ikke de vinkler, der svarer til kuglens vinkler, og de bevarer heller ikke perspektiv eller ækvivalens.
Det blev foreslået i 1772 af den schweiziske matematiker og geograf med samme navn. Dets hovedkarakteristik er, at den bruger en kegle tangent eller sekant til kuglen, og fremspringet holder vinklerne uændrede. Disse kvaliteter gør det meget nyttigt i luftfartstab..
United States Geological Survey (USGS) bruger Lambert Conic-projektionen. I denne projektion er afstandene sande langs standardparallellerne.
I Lambert-konisk projektion forbliver retningerne ret rimelige. Områderne og formerne er let forvrængede i positioner tæt på standardparallellerne, men ændringen af form og areal øges med adskillelse til dem..
Fordi formålet med denne projektion er at opretholde retninger og vinkler, der er lig med de originale på kuglen eller ellipsoiden, er der ingen geometrisk metode til at opnå den, i modsætning til den lige store projektion af Ptolemaios..
Det er snarere en analytisk projektionsmetode, der er baseret på matematiske formler.
USGS-basekortene til de 48 kontinentale stater bruger 33ºN og 45ºN som standardparalleller, hvilket giver en maksimal kortfejl på 2,5%..
For navigationskort i Alaska er de anvendte basisparalleller 55ºN og 65ºN. I stedet bruger det nationale atlas i Canada 49ºN og 77ºN.
Endnu ingen kommentarer