
Hvad er spændingsdeleren? (med eksempler)
Det spændingsdeler eller spændingsdeler består af en sammenslutning af modstande eller impedanser i serie forbundet med en kilde. På denne måde spændingen V leveret af kilden - indgangsspænding - fordeles proportionalt i hvert element i henhold til Ohms lov:
Vjeg = I.Zjeg.
Hvor Vjeg er spændingen på tværs af kredsløbselementet, jeg er strømmen, der strømmer gennem det og Zjeg den tilsvarende impedans.
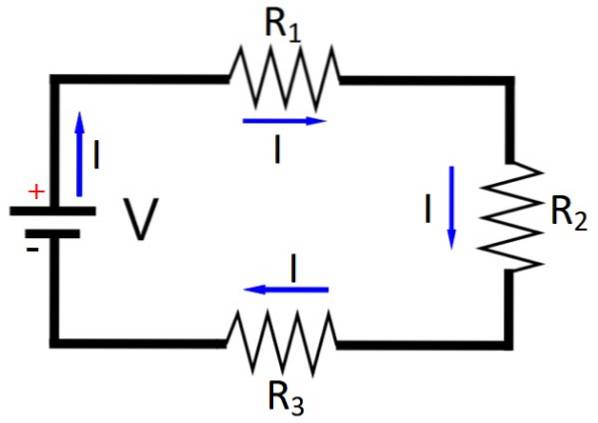
Når kilden og elementerne arrangeres i et lukket kredsløb, skal Kirchhoffs anden lov være opfyldt, som siger, at summen af al spænding falder og stiger er lig med 0.
For eksempel, hvis kredsløbet, der skal overvejes, er rent modstandsdygtigt, og en 12 volt kilde er tilgængelig, simpelthen ved at placere to identiske modstande i serie med kilden, vil spændingen blive delt: hver modstand vil have 6 volt. Og med tre identiske modstande opnås 4 V i hver enkelt.
Da kilden repræsenterer en spændingsstigning, så er V = +12 V. Og i hver modstand er der spændingsfald, der er repræsenteret af negative tegn: - henholdsvis - 6 V og - 6 V. Det er let at se, at Kirchoffs anden lov er opfyldt:
+12 V - 6 V - 6 V = 0 V
Det er her navnet på spændingsdeleren kommer fra, fordi der ved hjælp af seriemodstande let kan opnås lavere spændinger startende fra en kilde med en højere spænding.
Artikelindeks
- 1 Spændingsdelerligningen
- 1.1 Spændingsdeler med 2 modstande
- 2 Arbejdede eksempler
- 2.1 - Eksempel 1
- 2.2 - Eksempel 2
- 3 Referencer
Spændingsdelerligningen
Lad os fortsætte med at overveje et rent resistivt kredsløb. Vi ved, at strømmen I, der går gennem et kredsløb af modstande i serie forbundet med en kilde som vist i figur 1, er den samme. Og ifølge Ohms lov og Kirchoffs anden lov:
V = IR1 + AT GÅto + AT GÅ3 +… AT GÅjeg
Hvor R1, Rto... Rjeg repræsenterer hver seriemodstand i kredsløbet. Derfor:
V = I ∑ Rjeg
Så strømmen viser sig at være:
I = V / ∑ Rjeg
Lad os nu beregne spændingen over en af modstandene, modstanden Rjeg for eksempel:
Vjeg = (V / ∑ Rjeg) Rjeg
Den forrige ligning omskrives som følger, og vi har spændingsdelerreglen klar til et batteri og N-modstande i serie:
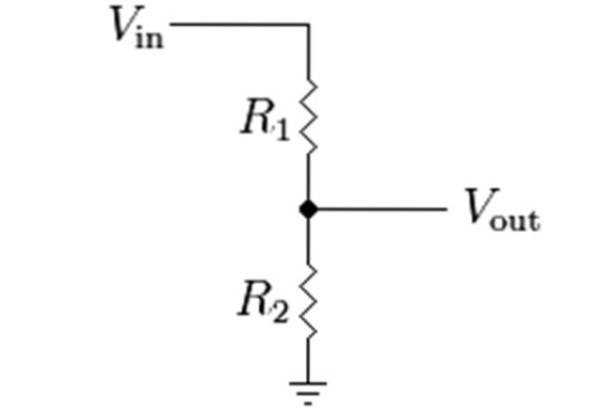
Spændingsdeler med 2 modstande
Hvis vi har et spændingsdelerkredsløb med 2 modstande, bliver ovenstående ligning:

Og i det specielle tilfælde hvor R1 = Rto, Vjeg = V / 2, uanset strøm, som angivet i starten. Dette er den enkleste spændingsdeler af alle.
I den følgende figur er diagrammet for denne skillevæg, hvor V, indgangsspændingen, er symboliseret som Vi, og Vjeg er spændingen opnået ved at dividere spændingen mellem modstandene R1 og Rto.

Arbejdede eksempler
Spændingsdelerreglen vil blive anvendt i to resistive kredsløb for at opnå lavere spændinger.
- Eksempel 1
En 12 V kilde er tilgængelig, som skal opdeles i 7 V og 5 V ved hjælp af to modstande R1 og Rto. Der er en 100 Ω fast modstand og en variabel modstand, hvis område er mellem 0 og 1 kΩ. Hvilke muligheder er der for at konfigurere kredsløbet og indstille værdien af modstanden Rto?
Opløsning
For at løse denne øvelse anvendes spændingsdelerreglen for to modstande:

Antag at R1 er modstanden fundet ved en spænding på 7 V, og der er den faste modstand R placeret1 = 100 Ω
Den ukendte modstand Rto skal være ved 5 V:

Og R1 ved 7 V:

5 (Rto +100) = 12 Rto
500 = 7 Rto
Rto = 71,43 Ω
På samme måde kan du bruge den anden ligning til at opnå den samme værdi eller erstatte det opnåede resultat for at kontrollere ligestilling.
Hvis nu den faste modstand er placeret som Rto, så bliver det R1 er ved 7 V:


5 (100 + R.1) = 100 x 12
500 + 5R1 = 1200
R1 = 140 Ω
På samme måde er det muligt at kontrollere, at denne værdi opfylder den anden ligning. Begge værdier er i det variable modstandsområde, derfor er det muligt at implementere det ønskede kredsløb på begge måder.
- Eksempel 2
Et jævnstrøms voltmeter til måling af spændinger i et bestemt område er baseret på spændingsdeleren. For at bygge et sådant voltmeter kræves et galvanometer, for eksempel D'Arsonval.
Det er en måler, der registrerer elektriske strømme, udstyret med en gradueret skala og en indikationsnål. Der er mange modeller af galvanometre, den i figuren er en meget enkel med to tilslutningsterminaler på bagsiden..

Galvanometeret har en intern modstand RG, der kun tåler en lille strøm, kaldet maksimal strøm IG. Derfor er spændingen over galvanometeret V.m = JegGRG.
For at måle enhver spænding placeres voltmeteret parallelt med det element, der skal måles, og dets interne modstand skal være stor nok til ikke at trække strøm fra kredsløbet, ellers vil det ændre det..
Hvis vi vil bruge galvanometeret som en måler, må den spænding, der skal måles, ikke overstige det maksimalt tilladte, hvilket er den maksimale afbøjning af nålen, som enheden har. Men vi antager, at Vm er lille, da jegG og RG de er.
Når galvanometeret imidlertid er forbundet i serie med en anden modstand RS, opkald begrænsende modstand, vi kan udvide måleområdet for galvanometeret fra det lille V.m op til en bestemt højere spænding ε. Når denne spænding er nået, oplever instrumentnålen maksimal afbøjning.
Designskemaet er som følger:
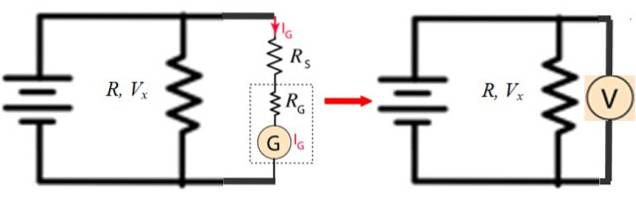
I figur 4 til venstre er G galvanometeret, og R er enhver modstand, som du vil måle spændingen V overx.
Figuren til højre viser, hvordan kredsløbet med G, RG og RS svarer til et voltmeter, der er placeret parallelt med modstanden R.
1V fuldskala voltmeter
Antag for eksempel, at galvanometerets interne modstand er RG = 50 Ω, og den maksimale strøm, den understøtter, er IG = 1 mA, den begrænsende modstand RS for voltmeteret bygget med dette galvanometer til måling af en maksimal spænding på 1 V beregnes som følger:
jegG (RS + RG) = 1 V.
RS = (1 V / 1 x 10-3 A) - RG
RS = 1000 Ω - 50 Ω = 950 Ω
Referencer
- Alexander, C. 2006. Grundlæggende om elektriske kredsløb. 3. Udgave. Mc Graw Hill.
- Boylestad, R. 2011. Introduktion til kredsløbsanalyse. 2. plads Udgave. Pearson.
- Dorf, R. 2006. Introduktion til elektriske kredsløb. 7. Udgave. John Wiley & Sons.
- Edminister, J. 1996. Elektriske kredsløb. Schaum-serien. 3. Udgave. Mc Graw Hill
- Figueroa, D. Physics Series for Sciences and Engineering. Vol. 5 elektrostatik. Redigeret af D. Figueroa. USB.
- Hyperfysik. Design af et voltmeter. Gendannet fra: hyperphysics.phy-astr.gsu.edu.
- Wikipedia. Spændingsdeler. Gendannet fra: es.wikipedia.org.



Endnu ingen kommentarer