
Hvad er dynamisk ligevægt? (Med eksempel)
Det dynamisk balance Det er den tilstand, hvor et bevægeligt objekt ideelt er repræsenteret som en partikel, når dets bevægelse er ensartet retlinet. Dette fænomen opstår, når summen af eksterne kræfter, der virker på det, annulleres..
Det antages ofte, at hvis der ikke er nogen netto eller resulterende kraft på et objekt, er hvile den eneste mulige konsekvens. Eller også at for at et legeme skal være i balance, må der ikke være nogen kraft, der virker.
-

Figur 1. Denne kat bevæger sig i dynamisk ligevægt, hvis den bevæger sig med konstant hastighed. Kilde: Pixabay.
I virkeligheden er ligevægt fraværet af acceleration, og derfor er konstant hastighed perfekt mulig. Katten i figuren bevæger sig muligvis uden acceleration.
Et objekt med ensartet cirkulær bevægelse er ikke i dynamisk ligevægt. Selvom dens hastighed er konstant, er der en acceleration rettet mod centrum af omkredsen, der holder den på stien. Denne acceleration er ansvarlig for at ændre hastighedsvektoren korrekt.
Nulhastigheden er en bestemt situation for en partikels ligevægt, svarende til at bekræfte, at objektet er i ro.
Hvad angår betragtning af objekter som partikler, er dette en meget nyttig idealisering, når man beskriver deres globale bevægelse. I virkeligheden er de bevægelige objekter, der omgiver os, sammensat af et stort antal partikler, hvis individuelle undersøgelse ville være besværlig..
Artikelindeks
- 1 Princippet om superposition
- 2 Rotations- og ligevægtsbetingelser
- 2.1 Moment eller moment af en kraft
- 2.2 Ligevægtsbetingelser for et udvidet objekt
- 2.3 Løsning
- 3 Referencer
Princippet om superposition
Dette princip gør det muligt at erstatte virkningen af flere kræfter på et objekt med en ækvivalent kaldet resulterende kraft FR eller nettokraft FN, som i dette tilfælde er nul:
F1 + F2 + F3 +…. = FR = 0
Hvor kræfterne F1, F2, F3…., Fi er de forskellige kræfter, der virker på kroppen. Summationsnotationen er en kompakt måde at udtrykke den på:
Så længe en ubalanceret kraft ikke griber ind, kan objektet bevæge sig på ubestemt tid med konstant hastighed, da kun en kraft kan ændre dette panorama.
Med hensyn til komponenterne i den resulterende kraft udtrykkes betingelsen for en partikels dynamiske ligevægt som følger: Fx = 0; Fy = 0; Fz = 0.
Rotations- og ligevægtsbetingelser
For partikelmodellen er betingelsen FR = 0 tilstrækkelig garanti for ligevægt. Men når man tager højde for dimensionerne på den mobile enhed, der undersøges, er der muligheden for, at objektet kan rotere.
Rotationsbevægelsen indebærer eksistensen af en acceleration, derfor er de roterende kroppe ikke i dynamisk ligevægt. Drejning af et legeme kræver ikke kun deltagelse af en styrke, men det er nødvendigt at anvende det på et passende sted.
For at kontrollere dette kan en tynd stang i længden placeres på en friktionsfri overflade, såsom en frossen overflade eller et højpoleret spejl eller glas. Normalen afbalancerer vægten lodret, og ved at påføre to kræfter F1 og F2 af samme størrelse vandret i henhold til diagrammet i den følgende figur, bekræftes hvad der sker:
-
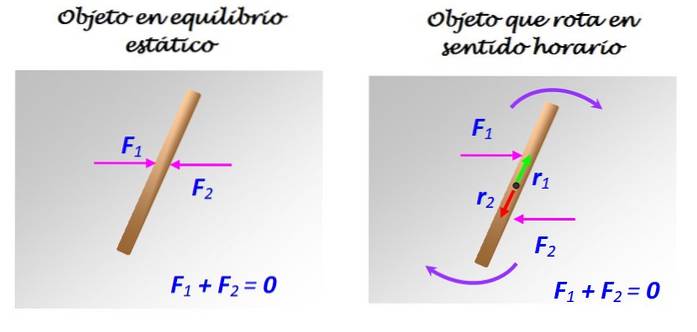
Figur 2. En stang på en friktionsfri overflade kan eller ikke være i ligevægt, afhængigt af hvordan kræfterne 1 og 2. påføres. Kilde: egen udførelse.
Hvis F1 og F2 anvendes som vist til venstre med en fælles handlingslinje, vil stangen forblive i ro. Men hvis F1 og F2 anvendes som vist til højre med forskellige handlingslinjer, selvom de er parallelle, sker der en rotation med uret omkring aksen, der passerer gennem midten.
I dette tilfælde udgør F1 og F2 et par kræfter eller blot et par.
Moment eller moment af en kraft
Virkningen af drejningsmoment er at producere en rotation på en udvidet genstand som stangen i eksemplet. Vektorens størrelsesstyrke kaldes drejningsmoment eller også moment af en kraft. Det betegnes som τ og beregnes af:
τ = r x F
I dette udtryk er F den påførte kraft, og r er vektoren, der går fra rotationsaksen til kraftens påføringspunkt (se figur 2). Retningen af τ er altid vinkelret på det plan, hvor F og r ligger, og dens enheder i det internationale system er N.m.
For eksempel er retningen af de øjeblikke, der produceres af F1 og F2, mod papiret i henhold til reglerne for vektorproduktet.
Selvom kræfterne annullerer hinanden, gør deres drejningsmomenter det ikke. Og resultatet er den viste rotation.
Ligevægtsbetingelser for et udvidet objekt
Der er to betingelser, der skal være opfyldt for at garantere balancen mellem et udvidet objekt:
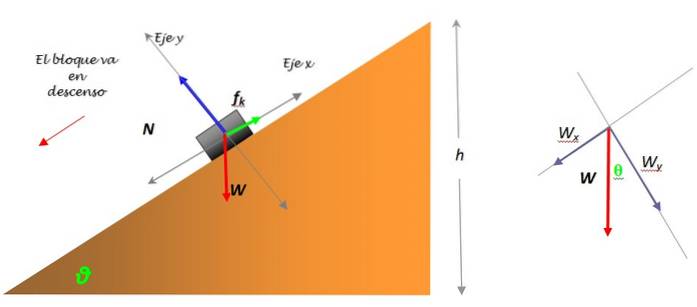
Der er en kasse eller bagagerum, der vejer 16 kg-f, som glider ned ad et skråt plan med konstant hastighed. Kilens hældningsvinkel er θ = 36º. Svar:
a) Hvad er størrelsen af den dynamiske friktionskraft, der er nødvendig for at bagagerummet glider med konstant hastighed?
b) Hvor meget er kinetisk friktionskoefficient?
c) Hvis højden h af det skråplan er 3 meter, skal du finde bagagerumets nedstigningshastighed og vide, at det tager 4 sekunder at nå jorden.
Opløsning
Bagagerummet kan behandles som om det var en partikel. Af denne grund vil kræfterne blive påført et sted, der ligger omtrent i dets centrum, hvor al dens masse kan antages at være koncentreret. Det er på dette tidspunkt, du bliver sporet.
-

Figur 3. Diagram med frit krop for bagagerum, der glider ned ad bakke og vægtnedbrydning (til højre). Kilde: selvfremstillet.
Vægten W er den eneste kraft, der ikke falder på en af koordinatakserne og skal nedbrydes i to komponenter: Wx og Wy. Denne nedbrydning er vist i diagrammet (figur 3).
Det er også praktisk at overføre vægten til enheder i det internationale system, for hvilket det er nok at gange med 9,8:
Wy = W. cosθ = 16 x 9,8 x cos 36º N = 126,9 N
Wx = W. sinθ = 16 x 9,8 x sin 36º = 92,2 N
Punkt a
Langs den vandrette akse er den vandrette komponent af vægten Wx og den dynamiske eller kinetiske friktionskraft fk, som modsætter sig bevægelsen.
Ved at vælge den positive retning i retning af bevægelsen er det let at se, at Wx er ansvarlig for, at blokken går ned ad bakke. Og da friktion modsættes, i stedet for at glide hurtigt, har blokken muligheden for at glide med konstant hastighed ned ad bakke.
Den første ligevægtstilstand er tilstrækkelig, da vi behandler bagagerummet som en partikel, hvilket vi er sikre på i udsagnet om, at det er i dynamisk ligevægt:
Wx - fk = 0 (ingen acceleration i vandret retning)
fk = 92,2 N
Afsnit b
Størrelsen af den dynamiske friktion er konstant og er givet af fk = μk N. Dette betyder, at den dynamiske friktionskraft er proportional med det normale, og størrelsen af dette kræves for at kende friktionskoefficienten.
Ved at observere det frie legemsdiagram kan det ses, at vi på den lodrette akse har den normale kraft N, som kilen udøver på bagagerummet og er rettet opad. Hun er afbalanceret med den lodrette del af vægten Wy. At vælge op som en positiv sans og gøre brug af Newtons anden lov og ligevægtstilstand resulterer:
N - Wy = 0 (der er ingen bevægelse langs den lodrette akse)
Derfor:
N = Wy = 126,9 N
fk = μk N
μk = fk / N = 92,2 /126,9= 0,73
Afsnit c
Den samlede afstand, som kufferten har kørt fra toppen af kilen til jorden, findes ved trigonometri:
d = h / sin 36º = 3 / sin 36º m = 5,1 m.
For at beregne hastigheden anvendes definitionen for ensartet retlinet bevægelse:
v = d / t = 5,1 m / 4 s = 1,3 m / s
Referencer
- Rex, A. 2011. Grundlæggende fysik. Pearson. 76 - 90.
- Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 1. 7. Ed. Cengage Learning. 120 - 124.
- Serway, R., Vulle, C. 2011. Fundamentals of Physics. 9. udgave Cengage Learning. 99-112.
- Tippens, P. 2011. Fysik: begreber og applikationer. 7. udgave. MacGraw Hill. 71 - 87.
- Walker, J. 2010. Fysik. Addison Wesley. 148-164.



Endnu ingen kommentarer