
Hvad er modulet for forskydning, stivhed eller forskydning? (Øvelser løst)
Det skæremodul beskriver reaktionen fra et materiale på påføringen af en forskydningsspænding, der deformerer det. Andre hyppigt anvendte navne på forskydningsmodul er forskydningsmodul, forskydningsmodul, tværgående elasticitet eller tangentiel elasticitet..
Når spændingerne er små, er deformationerne proportionale med dem ifølge Hookes lov, hvor forskydningsmodulet er konstanten af proportionaliteten. Derfor:
Forskydningsmodul = Forskydningsspænding / belastning
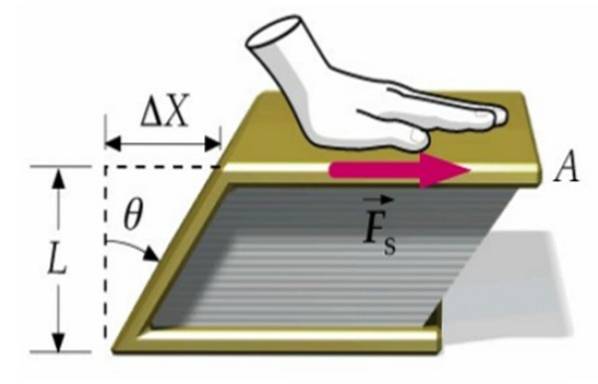
Antag, at den ene kraft påføres omslaget til en bog, mens den anden er fastgjort på overfladen af bordet. På denne måde bevæger bogen sig som helhed ikke, men deformeres, når det øverste omslag bevæger sig i forhold til det nederste med mængden Δx.
Bogen går fra at have et rektangulært tværsnit til et parallelogramformet snit, som vi ser på billedet ovenfor.
Være:
τ = F / A
Forskydningsspændingen eller spændingen, væren F størrelsen af den påførte kraft og TIL det område, som det handler på.
Deformationen forårsaget af kvotienten:
δ = Δx / L
Derfor er forskydningsmodulet, som vi vil betegne som G:

Og da Δx / L ikke har nogen dimensioner, er enhederne af G de samme som forskydningsspændingen, hvilket er forholdet mellem kraft og areal..
I det internationale enhedssystem er disse enheder Newton / kvadratmeter eller pascal, forkortet Pa. Og i angelsaksiske enheder er det pund / kvadrat tomme, forkortet psi.
Artikelindeks
- 1 Skæremodul til forskellige materialer
- 1.1 Eksperimentel måling af forskydningsmodul
- 1.2 Sådan finder du G?
- 2 Øvelser med løsning
- 2.1 - Øvelse 1
- 2.2 - Øvelse 2
- 3 Referencer
Skæremodul til forskellige materialer
Under påvirkning af forskydningskræfter som de beskrevne tilbyder genstandene en modstand svarende til bogen, hvor de indre lag glider. Denne form for deformation kan kun forekomme i faste kroppe, som har tilstrækkelig stivhed til at modstå deformation..
På den anden side tilbyder væsker ikke denne form for modstand, men de kan gennemgå volumendeformationer.

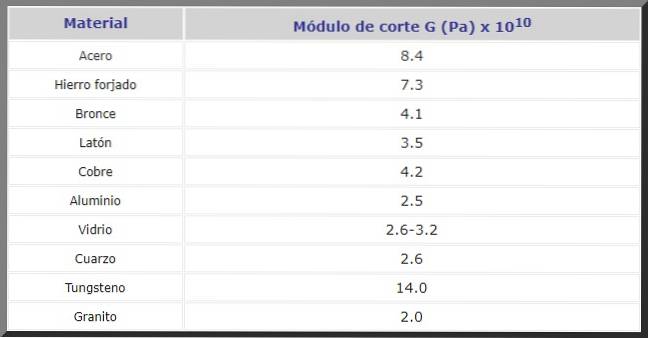
Nedenfor er G in Pa skæremodul til forskellige materialer, der ofte bruges i konstruktion og til fremstilling af maskiner og reservedele af enhver art:
Eksperimentel måling af forskydningsmodul
For at finde værdien af forskydningsmodulet skal prøver af hvert materiale testes, og deres svar på anvendelsen af en forskydningsspænding undersøges..
Prøven er en stang lavet af materialet med radius R og længde L kendt, som er fastgjort i den ene ende, mens den anden er forbundet med akslen på en remskive, der er fri til at rotere.
Remskiven er bundet med et reb, i hvis frie ende der hænges en vægt, der udøver en kraft F på stangen gennem rebet. Og denne kraft producerer igen et øjeblik M på stangen, som derefter roterer en lille vinkel θ.
Et diagram over samlingen kan ses i følgende figur:
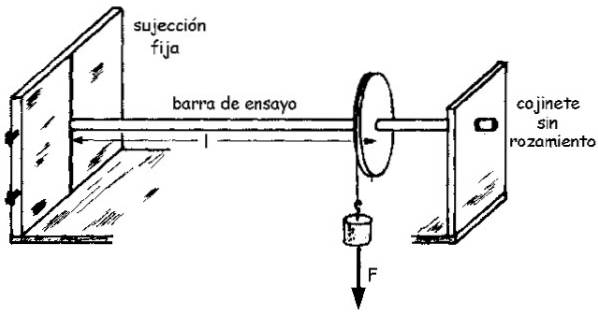
Øjeblikkets størrelse M, som vi betegner som M (ingen fed) er relateret til den roterede vinkel θ gennem forskydningsmodulet G ifølge følgende ligning (udledt af en simpel integral):

Da momentets størrelse er lig med produktet af modulet af kraften F og remskiven R's radiuss:
M = F.Rs
Og styrke er den vægt, der hænger W, derefter:
M = W.Rs
Udskiftning af ligningen for øjeblikkets størrelse:

Der er forholdet mellem vægt og vinkel:

Sådan finder du G?
Dette forhold mellem variablerne W Y θ er lineær, så de forskellige vinkler, der produceres ved at hænge forskellige vægte, måles.
Vægt- og vinkelparene er afbildet på grafpapir, den bedste linje, der passerer gennem de eksperimentelle punkter, monteres, og hældningen beregnes. m af nævnte linje.


Øvelser med løsning
- Øvelse 1
En stang 2,5 meter lang og radius 4,5 mm er fastgjort i den ene ende. Den anden er forbundet med en 75 cm radius remskive, der har en hængende vægt W på 1,3 kg. Den roterede vinkel er 9,5º.
Med disse data anmodes det om at beregne stangens forskydningsmodul G.
Opløsning
Fra ligningen:

G er ryddet:

Og værdierne i erklæringen erstattes, idet man sørger for at udtrykke alle data i det internationale system for enheder SI:
R = 4,5 mm = 4,5 x 10 -3 m
Rs = 75 cm = 0,075
At gå fra kilogram (som faktisk er kg - kraft) til newton ganges med 9,8:
W = 1,3 kg kraft = 1,3 x 9,8 N = 12,74 N.
Og endelig skal graderne være i radianer:
9,5 º = 9,5 x2π / 360 radianer = 0,1665 radianer.
Med alt dette har du:

= 2.237 x 1010 Pa
- Øvelse 2
En terning lavet af gel har en side på 30 cm. Den ene af dens ansigter er fast, men samtidig påføres en parallel kraft på 1 N på den modsatte side, som takket være den bevæger sig 1 cm (se eksemplet på bogen i figur 1).
Det anmodes om at beregne med disse data:
a) Størrelsen af forskydningsspændingen
b) Stamme δ
c) Værdien af forskydningsmodulet
Løsning til
Forskydningsspændingens størrelse er:
τ = F / A
Med:
A = sideto = (30 x 10-to cm)to = 0,09 mto
Derfor:
τ = 1 N / 0,09 mto = 11,1 Pa
Løsning b
Stamme er ingen ringere end værdien af δ, givet af:
δ = Δx / L
Forskydningen af ansigtet, der udsættes for kraften, er 1 cm, derefter:
δ = 1/30 = 0,0333
Løsning c
Forskydningsmodulet er kvotienten mellem forskydningsspændingen og belastningen:
G = forskydningsspænding / belastning
Derfor:
G = 11,1 Pa / 0,033 = 336,4 Pa
Referencer
- Beer, F. 2010. Mekanik af materialer. McGraw Hill. 5. plads Udgave.
- Franco García, A. Solid Rigid. Måling af forskydningsmodul. Gendannet fra: sc.ehu.es.
- Giancoli, D. 2006. Fysik: Principper med applikationer. 6. Ed prentice hall.
- Resnick, R. (1999). Fysisk. Bind 1. 3. udgave på spansk. Compañía Editorial Continental S.A. af C.V.
- University of Valladolid. Institut for Fysik for kondenseret materiale. Valg af problemer. Gendannet fra: www4.uva.es.



Endnu ingen kommentarer