
Hvad er dalen i fysik? (med eksempler)
Det dal i fysik Det er en betegnelse, der anvendes i studiet af bølgefænomener for at angive den mindste eller laveste værdi af en bølge. Således betragtes en dal som en konkavitet eller depression.
I tilfælde af den cirkulære bølge, der dannes på vandoverfladen, når en dråbe eller en sten falder, er fordybningerne bølgedalene, og bulerne er rygge.

Et andet eksempel er den bølge, der genereres i en stram streng, hvor den ene ende er lavet til at svinge lodret, mens den anden holdes fast. I dette tilfælde forplantes den producerede bølge med en vis hastighed, har en sinusform og består også af dale og højderyg..
Ovenstående eksempler henviser til tværgående bølger, fordi dale og kamme løber på tværs eller vinkelret på udbredelsesretningen..
Imidlertid kan det samme koncept anvendes på langsgående bølger såsom lyd i luften, hvis svingninger forekommer i samme formeringsretning. Her vil bølgedalene være de steder, hvor luftens tæthed er minimal og rygge, hvor luften er mere tæt eller komprimeret.
Artikelindeks
- 1 Parametre for en bølge
- 1.1 Dale og højderyg i en harmonisk bølge
- 2 Eksempel på dale: tørresnoren
- 2.1 Harmonisk bølgefunktion for strengen
- 2.2 Dalenes placering på rebet
- 3 Referencer
Parametre for en bølge
Afstanden mellem to dale eller afstanden mellem to kamme kaldes bølgelængde og betegnes med det græske bogstav λ. Det samme punkt i en bølge skifter fra at være i en dal til at være et kam, når svingningen udbreder sig.
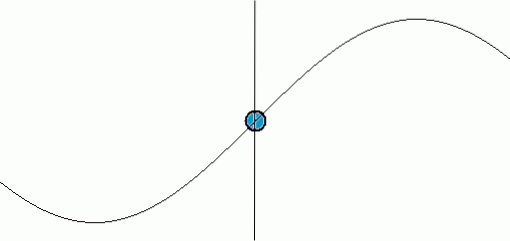
Den tid, der går fra en dal-kam-dal, i en fast position, kaldes svingeperiode og denne gang er betegnet med store bogstaver: T.
I en periode T bølgen bevæger sig en bølgelængde λ, Derfor siges det hastighed v hvormed bølgen skrider frem er:
v = λ / T
Adskillelsen eller den lodrette afstand mellem dalen og toppen af en bølge er dobbelt så meget som svingningens amplitude, dvs. afstanden fra en dal til midten af den lodrette svingning er amplitude A. bølge.
Dale og højderyg i en harmonisk bølge
En bølge er harmonisk, hvis dens form er beskrevet af de matematiske funktioner sinus eller cosinus. Generelt er en harmonisk bølge skrevet som:
y (x, t) = A cos (k⋅x ± ω⋅t)
I denne ligning er variablen Y repræsenterer afvigelsen eller forskydningen fra ligevægtspositionen (y = 0) ved position x I øjeblikket t.
Parameter TIL er svingningens amplitude, en altid positiv størrelse, der repræsenterer afvigelsen fra bølgedalen til svingningens centrum (y = 0). I en harmonisk bølge er det tilfreds, at afvigelsen Y, fra dalen til højderyggen er det A / 2.
Bølgenummer
Andre parametre, der vises i den harmoniske bølgeformel, specifikt i argumentet for sinusfunktionen, er bølgetallet k og vinkelfrekvensen ω.
Bølgenummer k er relateret til bølgelængde λ ved hjælp af følgende udtryk:
k = 2π / λ
Vinkelfrekvens
Vinkelfrekvens ω er relateret til perioden T igennem:
ω = 2π / T
Bemærk, at ± vises i argumentet for sinusfunktionen, det vil sige i nogle tilfælde anvendes det positive tegn og i andre det negative tegn.
Hvis en bølge formerer sig i den positive retning af x, så er det minustegnet (-), der skal anvendes. Ellers, dvs. i en bølge, der formerer sig i negativ retning, påføres det positive tegn (+)..
Harmonisk bølgehastighed
Formationshastigheden for en harmonisk bølge kan skrives som en funktion af vinkelfrekvensen og bølgetallet som følger:
v = ω / k
Det er let at vise, at dette udtryk er fuldstændig ækvivalent med det, vi gav tidligere som en funktion af bølgelængde og periode.
Daleeksempel: tørresnoren
Et barn spiller bølger med rebet på en tøjlinje, som han løsner den ene ende for og får det til at svinge med en lodret bevægelse med en hastighed på 1 svingning pr. Sekund.
Under denne proces forbliver barnet stille på det samme sted og bevæger kun armen op og ned og omvendt..
Mens drengen genererer bølgerne, tager hans ældre bror et billede af ham med sin mobil. Når du sammenligner størrelsen på bølgerne med bilen, der er parkeret lige bag rebet, bemærker du, at den lodrette adskillelse mellem dale og højderyg er den samme som højden på bilvinduerne (44 cm).
På billedet kan det også ses, at adskillelsen mellem to på hinanden følgende dale er den samme som mellem bagkanten af bagdøren og frontkanten af hoveddøren (2,6 m).
Harmonisk bølgefunktion for strengen
Med disse data foreslår den ældre bror at finde den harmoniske bølgefunktion, idet den antager som det første øjeblik (t = 0) det øjeblik, hvor hans lillebrors hånd var på det højeste punkt..
Det antages også, at x-aksen starter (x = 0) på håndstedet med en positiv fremadgående retning og passerer gennem midten af den lodrette svingning. Med denne information kan du beregne parametrene for den harmoniske bølge:
Amplituden er halvdelen af en dals højde til en højderyg, det vil sige:
A = 44 cm / 2 = 22 cm = 0,22 m
Bølgetallet er
k = 2π / (2,6 m) = 2,42 rad / m
Når barnet løfter og sænker hånden i løbet af et sekund, vil vinkelfrekvensen være
ω = 2π / (1 s) = 6,28 rad / s
Kort sagt er formlen for den harmoniske bølge
y (x, t) = 0,22m cos (2,42⋅x - 6.28⋅t)
Udbredelseshastigheden for bølgen vil være
v = 6,28 rad / s/ 2,42 rad / m = 15,2 m / s
Dalenes placering på rebet
Den første dal inden for et sekund efter start af håndbevægelsen vil være på afstand d af barnet og givet af følgende forhold:
y (d, 1s) = -0,22m = 0,22m cos (2,42d - 6.28⋅1)
Hvilket betyder at
cos (2,42d - 6,28) = -1
Nemlig
2,42⋅d - 6,28 = -π
2.42⋅d = π
d = 1,3 m (position af dalen nærmest t = 1s)
Referencer
- Giancoli, D. Fysik. Principper med applikationer. 6. udgave. Prentice Hall. 80-90
- Resnick, R. (1999). Fysisk. Bind 1. tredje udgave på spansk. Mexico. Compañía Editorial Continental S.A. de C.V. 100-120.
- Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 1. 7. Udgave. Mexico. Cengage Learning Editors. 95-100.
- Strenge, stående bølger og harmoniske. Gendannet fra: newt.phys.unsw.edu.au
-
Bølger og mekaniske enkle harmoniske bølger. Gendannet fra: physicskey.com.


Endnu ingen kommentarer