
Hvad er akustisk impedans? Ansøgninger og øvelser
Det akustisk impedans eller specifik akustisk impedans er materialemediets modstand mod passage af lydbølger. Det er konstant for et bestemt medium, der går fra et stenet lag i det indre af jorden til det biologiske væv.
Betegner den akustiske impedans som Z, i matematisk form har vi:
Z = ρ.v
Hvor ρ er densiteten og v lydens hastighed på mediet. Dette udtryk er gyldigt for en plan bølge, der bevæger sig i en væske.
I SI International System-enheder er densiteten i kg / m3 og hastigheden i m / s. Derfor er enhederne med akustisk impedans kg / mto.s.
Ligeledes er den akustiske impedans defineret som kvotienten mellem trykket p og hastigheden:
Z = p / v
Udtrykt på denne måde er Z analog med elektrisk modstand R = V / I, hvor tryk spiller rollen som spænding og hastighed for strømmen. Andre SI-enheder af Z ville være Pa.s / m eller N.s / m3, fuldstændig svarende til dem, der er givet tidligere.
Artikelindeks
- 1 Transmission og refleksion af lydbølgen
- 1.1 Transmissions- og reflektionskoefficienter
- 2 Ansøgninger og øvelser
- 2.1 - Øvelse løst 1
- 2.2 - Øvelse løst 2
- 3 Referencer
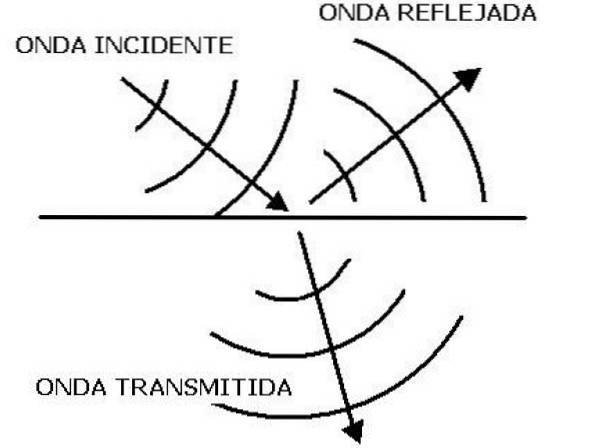
Lydbølgetransmission og refleksion
Når du har to midler til forskellige impedanser Z1 og Zto, en del af en lydbølge, der rammer begge grænseflader, kan overføres, og en anden del kan reflekteres. Denne reflekterede bølge eller ekko er den, der indeholder vigtig information om det andet medium..
Den måde, hvorpå energien transporteret af bølgen fordeles, afhænger af reflektionskoefficienterne R og transmissionskoefficienten T, to meget nyttige størrelser til at studere lydbølgens forplantning. For reflektionskoefficienten er det kvotienten:
R = Ir / Jegeller
Hvor jegeller er intensiteten af hændelsesbølgen og jegr er intensiteten af den reflekterede bølge. På samme måde har vi transmissionskoefficienten:
T = It / Jegeller
Nu kan det vises, at intensiteten af en plan bølge er proportional med dens amplitude A:
I = (1/2) Z.ωto .TILto
Hvor Z er den akustiske impedans af mediet, og ω er bølgefrekvensen. På den anden side er kvotienten mellem den transmitterede amplitude og den indfaldende amplitude:
TILt/TILeller = 2Z1/ (Z1 +Zto)
Hvilket tillader kvotienten It / Jegeller udtrykkes i form af amplituden af hændelsen og transmitterede bølger som:
jegt / Jegeller = ZtoTILtto / Z1TILellerto
Ved hjælp af disse udtryk opnås R og T i form af den akustiske impedans Z.
Transmissions- og reflektionskoefficienter
Ovennævnte kvotient er netop transmissionskoefficienten:
T = (Zto/ Z1) [2.Z1/ (Z1 +Zto)]to = 4Z1Zto / (Z1 +Zto)to
Da der ikke overvejes tab, er det sandt, at hændelsesintensiteten er summen af den transmitterede intensitet og den reflekterede intensitet:
jegeller = Jegr + jegt → (Ir / Jegeller) + (It / Jegeller) = 1
Dette giver os mulighed for at finde et udtryk for refleksionskoefficienten med hensyn til de to mediers impedanser:
R + T = 1 → R = 1 - T
Ved at udføre en lille algebra for at omarrangere vilkårene er refleksionskoefficienten:
R = 1 - 4Z1Zto / (Z1 +Zto)to = (Z1 - Zto)to/ (Z1 +Zto)to
Og da informationen relateret til det andet medium findes i den reflekterede puls, er reflektionskoefficienten af stor interesse..
Når de to medier således har en stor forskel i impedans, bliver tælleren for det foregående udtryk større. Derefter er intensiteten af den reflekterede bølge høj og indeholder god information om mediet..
Hvad angår den del af bølgen, der transmitteres til det andet medium, falmer den gradvist, og energien spredes som varme..
Ansøgninger og øvelser
Transmissions- og refleksionsfænomener giver anledning til flere meget vigtige anvendelser, for eksempel ekkolod udviklet under anden verdenskrig og brugt til at opdage genstande. Forresten har nogle pattedyr som flagermus og delfiner et indbygget ekkolodssystem.
Disse egenskaber bruges også i vid udstrækning til at studere det indre af jorden i seismiske prospekteringsmetoder, i medicinsk ultralydsbilleddannelse, måling af knogletæthed og billeddannelse af forskellige strukturer for fejl og mangler..
Akustisk impedans er også en vigtig parameter, når man vurderer lydresponset på et musikinstrument..
- Løst øvelse 1
Ultralydsteknikken til billede af biologisk væv gør brug af højfrekvente lydimpulser. Ekkoerne indeholder information om de organer og væv, de passerer igennem, som en software er ansvarlig for at oversætte til et billede.
En ultralydspuls rettet mod fedt-muskel-grænsefladen er skåret. Find de data, du finder:
a) Den akustiske impedans af hvert væv.
b) Procentdelen af ultralyd reflekteret ved grænsefladen mellem fedt og muskler.
Fedt
- Massefylde: 952 kg / m3
- Lydhastighed: 1450 m / s
Muskel
- Massefylde: 1075 kg / m3
- Lydhastighed: 1590 m / s
Løsning til
Den akustiske impedans af hvert væv findes ved at erstatte i formlen:
Z = ρ.v
På denne måde:
Zfedt = 952 kg / m3 x 1450 m / s = 1,38 x 106 kg / mto.s
Zmuskel = 1075 kg / m3 x 1590 m / s = 1,71 x 106 kg / mto.s
Løsning b
For at finde den procentvise intensitet, der reflekteres ved grænsefladen mellem de to væv, anvendes reflektionskoefficienten givet af:
R = (Z1 - Zto)to/ (Z1 +Zto)to
Her Zfedt = Z1 og Zmuskel = Zto. Refleksionskoefficienten er en positiv størrelse, som er garanteret af kvadraterne i ligningen.
Udskiftning og evaluering:
R = (1,38 x 106 - 1,71 x 106 )to / (1,38 x 106 + 1,71 x 106 )to = 0,0114.
Når vi multiplicerer med 100, reflekteres procentdelen: 1,14% af hændelsesintensiteten.
- Træning løst 2
En lydbølge har et intensitetsniveau på 100 decibel og falder normalt på vandoverfladen. Bestem intensitetsniveauet for den transmitterede bølge og den for den reflekterede bølge.
Data:
Vand
- Massefylde: 1000 kg / m3
- Lydhastighed: 1430 m / s
Luft
- Massefylde: 1,3 kg / m3
- Lydhastighed: 330 m / s
Opløsning
Intensitetsniveauet i decibel af en lydbølge, betegnes som L, er dimensionsløst og er givet ved formlen:
L = 10 log (I / 10-12)
Hæve til 10 på begge sider:
10 L / 10 = I / 10-12
Da L = 100 resulterer det i:
I / 10-12 = 1010
Enhedsintensiteter er angivet i kraft pr. Arealenhed. I det internationale system er de Watt / mto. Derfor er intensiteten af den indfaldende bølge:
jegeller = 1010 . 10-12 = 0,01 W / mto.
For at finde intensiteten af den transmitterede bølge beregnes transmissionskoefficienten og derefter ganges med hændelsesintensiteten.
De respektive impedanser er:
ZVand = 1000 kg / m3 x 1430 m / s = 1,43 x 106 kg / mto.s
Zluft = 1,3 kg / m3 x 330 m / s = 429 kg / mto.s
Udskiftning og evaluering i:
T = 4Z1Zto / (Z1 +Zto)to = 4 × 1,43 x 106 x 429 / (1,43 x 106 + 429)to = 1,12 x 10-3
Så intensiteten af den transmitterede bølge er:
jegt = 1,12 x 10-3 x 0,01 W / mto = 1,12 x 10-5 W / mto
Dens intensitetsniveau i decibel beregnes af:
Lt = 10 log (It / 10-12) = 10 log (1,12 x 10-5 / 10-12) = 70,3 dB
Refleksionskoefficienten er for sin del:
R = 1 - T = 0,99888
Med dette er intensiteten af den reflekterede bølge:
jegr = 0,99888 x 0,01 W / mto = 9,99 x 10-3 W / mto
Og dens intensitetsniveau er:
Lt = 10 log (Ir / 10-12) = 10 log (9,99 x 10-3 / 10-12) = 100 dB
Referencer
- Andriessen, M. 2003. HSC Physics Course. Jacaranda.
- Baranek, L. 1969. Akustik. Anden version. Redaktionel Hispano Americana.
- Kinsler, L. 2000. Fundamentals of Acoustics. Wiley og sønner.
- Lowrie, W. 2007. Grundlæggende om geofysik. 2. plads Udgave. Cambridge University Press.
- Wikipedia. Akustisk impedans. Gendannet fra: en.wikipedia.org.



Endnu ingen kommentarer