Det deterministisk eksperiment, i statistik er det et, der har et forudsigeligt og reproducerbart resultat, så længe de samme indledende betingelser og parametre opretholdes. Det vil sige, forholdet mellem årsag og virkning er fuldt kendt.
For eksempel er det tid, det tager for et urs sand at bevæge sig fra det ene rum til det andet, et deterministisk eksperiment, fordi resultatet er forudsigeligt og reproducerbart. Så længe forholdene er de samme, vil det tage samme tid at rejse fra kapsel til kapsel.
Mange fysiske fænomener er deterministiske, hvoraf nogle eksempler er følgende:
- En genstand, der er tættere end vand, såsom en sten, vil altid synke.
- En flyder, der er mindre tæt end vand, vil altid flyde op (medmindre der udøves en kraft for at holde den nedsænket).
- Vandets kogetemperatur ved havoverfladen er altid 100 ºC.
- Den tid det tager for en matrice, der falder fra hvile til fald, da den bestemmes af højden, hvorfra den blev droppet, og denne gang er altid den samme (når den falder fra samme højde).
Udnytte eksemplet med terningerne. Hvis det tabes, selv når man sørger for at give det samme retning og altid i samme højde, er det vanskeligt at forudsige, hvilken side det vil dukke op, når det er stoppet på jorden. Dette ville være et tilfældigt eksperiment.
Teoretisk, hvis data som: position var kendt med uendelig præcision; starthastighed og orientering af matricen; form (med afrundede eller kantede kanter); og restitutionskoefficient for overfladen, hvorpå den falder, måske ville det være muligt at forudsige ved komplekse beregninger, som vender mod matrisen, vil dukke op, når den stopper. Men enhver lille variation i startbetingelserne vil give et andet resultat..
Sådanne systemer er deterministiske og samtidig kaotiske, da en lille ændring af de oprindelige forhold ændrer det endelige resultat på en tilfældig måde..
Artikelindeks
Deterministiske eksperimenter er helt målbare, men alligevel er målingen af deres resultat ikke uendeligt præcis og har en vis usikkerhedsmargen.
Tag for eksempel følgende fuldstændig deterministiske eksperiment: smid en legetøjsbil ned ad et skrånende lige spor.
Det frigøres altid fra det samme udgangspunkt, og pas på ikke at give nogen impuls. I dette tilfælde skal den tid, det tager for bilen at køre på banen, altid være den samme.
Nu sætter et barn ud for at måle den tid, det tager for vognen at rejse på banen. Til dette vil du bruge stopuret, der er indbygget i din mobiltelefon.
At være en opmærksom dreng er det første, du bemærker, at dit måleinstrument har en begrænset præcision, fordi den mindste tidsforskel, som stopuret kan måle, er 1 hundrededel af et sekund..
Derefter fortsætter barnet med at udføre eksperimentet, og med det mobile stopur måler 11 gange - lad os sige for at være sikker - den tid, det tog for klapvognen at rejse det skrånende plan og opnå følgende resultater:
3.12s 3.09s 3.04s 3.04s 3.10s 3.08s 3.05s 3.10s 3.11s 3.06s og 3.03s.
Barnet er overrasket, fordi de i skolen havde fortalt ham, at dette er et deterministisk eksperiment, men i hver måling opnåede han et lidt andet resultat.
Hvad kan være årsagerne til, at hver måling har et andet resultat??
En årsag kan være instrumentets præcision, som som nævnt er 0,01 sek. Men bemærk, at forskellene i målingerne er over den værdi, så andre årsager skal overvejes, såsom:
- Små variationer fra udgangspunktet.
- Forskelle i stopurets start og pause på grund af barnets reaktionstid.
Med hensyn til reaktionstiden er der bestemt en forsinkelse, fra barnet ser, at vognen begynder at bevæge sig, indtil han trykker på stopuret..
Tilsvarende er der en ankomstforsinkelse på grund af tid til reaktionstid. Men start- og ankomstforsinkelserne kompenseres, så den opnåede tid skal være meget tæt på den sande..
Under alle omstændigheder er kompensationen for reaktionsforsinkelsen ikke nøjagtig, fordi reaktionstiderne kan have små variationer i hver test, hvilket forklarer forskellene i resultaterne..
Hvad er så det virkelige resultat af eksperimentet?
For at rapportere det endelige resultat skal vi bruge statistikker. Lad os først se, hvor ofte resultaterne gentages:
- 3.03s (1 gang)
- 3.04s (2 gange)
- 3.05s (1 gang)
- 3.06s (1 gang)
- 3.08s (1 gang)
- 3.09s 1 gang
- 3.10s (2 gange)
- 3.11s (1 gang)
- 3.12s (1 gang)
Når vi bestiller dataene, indser vi, at en mode eller flere gentagne resultater. Derefter er resultatet, der skal rapporteres, det aritmetiske gennemsnit, som kan beregnes således:
(1 × 3.03 + 2 × 3.04 + 1 × 3.05 + 1x 3.06 + 1 × 3.08 + 1 × 3.09 + 2 × 3.10 + 1 × 3.11 + 1 × 3.12) / (1 + 2 + 1 + 1 + 1 + 1 + 2 + 1 + 1).
Resultatet af ovenstående beregning er 3.074545455. Logisk set giver det ikke mening at rapportere alle disse decimaler i resultatet, fordi hver måling kun har 2 decimaler af præcision..
Anvendelse af afrundingsreglerne kan angives, at den tid det tager for vognen at køre på banen er det aritmetiske gennemsnit afrundet til to decimaler.
Resultatet, som vi kan rapportere til vores eksperiment er:
3,08 sekunder er den tid det tager for legetøjsbilen at køre skråningen.
Som vi har set i vores eksempel på et deterministisk eksperiment, har hver måling en fejl, da den ikke kan måles med uendelig præcision..
Under alle omstændigheder er det eneste, der kan gøres, at forbedre instrumenterne og målemetoderne for at opnå et mere præcist resultat..
I det foregående afsnit gav vi et resultat for vores deterministiske eksperiment med den tid, det tager for legetøjsbilen at køre et skrånende spor. Men dette resultat indeholder en fejl. Nu vil vi forklare, hvordan man beregner denne fejl.
I tidsmålingerne noteres en dispersion i de foretagne målinger. Det standardafvigelse er en form, der ofte bruges i statistikker til at rapportere spredning af data.
Måden at beregne standardafvigelsen på er sådan: først finder du variansen af data, defineret på denne måde:
Summen af forskellene i hvert resultat med det aritmetiske gennemsnit, kvadreret og divideret med det samlede antal data
Hvis variansen tages kvadratroden, opnås standardafvigelsen.
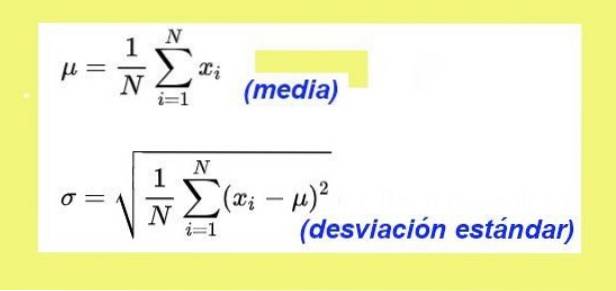
Standardafvigelsen for data om nedstigning af legetøjsbiler er:
σ = 0,03
Resultatet blev afrundet til 2 decimaler, fordi nøjagtigheden af hver af dataene er 2 decimaler. I dette tilfælde repræsenterer 0,03 sek den statistiske fejl for hver af dataene..
Imidlertid har det gennemsnitlige eller aritmetiske gennemsnit af de opnåede tider en mindre fejl. Den gennemsnitlige fejl beregnes ved at dividere standardafvigelsen med kvadratroden af det samlede antal data..
Gennemsnitlig fejl = σ / √N = 0,03 / √11 = 0,01
Det vil sige, at den statistiske fejl for tidsgennemsnittet er 1 hundrededel af et sekund, og i dette eksempel falder det sammen med appreciering af stopuret, men dette er ikke altid tilfældet..
Som et endeligt resultat af målingen rapporteres det derefter:
t = 3.08s ± 0.01s er den tid, det tager for legetøjsbilen at køre det skrå spor.
Det konkluderes, at selv når det er et deterministisk eksperiment, har resultatet af dets måling ikke uendelig præcision og har altid en fejlmargen..
Og også for at rapportere det endelige resultat er det nødvendigt, selv når det er et deterministisk eksperiment, at bruge statistiske metoder.
Endnu ingen kommentarer