
Hvad er en geoid?
Det geoid Jordens figur er den teoretiske overflade på vores planet, bestemt af havenes gennemsnitlige niveau og med en ret uregelmæssig form. Matematisk er det defineret som den ækvipotentiale overflade af Jordens effektive tyngdepotentiale ved havets overflade.
Da det er en imaginær (ikke-materiel) overflade, krydser den kontinenter og bjerge, som om alle have var forbundet med vandkanaler, der passerer gennem landmasser..

Jorden er ikke en perfekt sfære, da rotation omkring sin akse gør det til en slags kugle, der er fladt af polerne med dale og bjerge. Derfor er den sfæroide form stadig unøjagtig.
Den samme rotation tilføjer en centrifugalkraft til jordens tyngdekraft, hvis resulterende eller effektive kraft ikke peger på Jordens centrum, men har et vist tyngdepotentiale forbundet med det..
Hertil kommer, at de geografiske ulykker skaber uregelmæssigheder i densitet, og derfor ophører tyngdekraftens tiltrækningskraft i nogle områder helt sikkert med at være central..
Så forskere, der begyndte med C. F. Gauss, der udtænkte den oprindelige geoid i 1828, skabte en geometrisk og matematisk model for at repræsentere jordens overflade mere præcist..
Til dette antages et hav i hvile uden tidevand eller havstrømme og med konstant tæthed, hvis højde tjener som reference. Jordens overflade betragtes derefter som forsigtigt bølget, stiger hvor lokal tyngdekraft er størst og synker, når den falder.
Lad under disse forhold den effektive tyngdeacceleration altid være vinkelret på overfladen, hvis punkter har samme potentiale, og resultatet er geoiden, som er uregelmæssig, da ekvipotentialet ikke er symmetrisk.
Artikelindeks
- 1 Fysisk fundament for geoiden
- 1.1 Jordens tyngdepotentiale
- 2 Forskelle mellem geoid og ellipsoid
- 2.1 Geoidens bølger
- 3 Fordele ved at repræsentere Jorden som en geoid
- 4 Referencer
Geoidets fysiske fundament
For at bestemme geoidens form, som er blevet raffineret over tid, har forskere udført mange målinger under hensyntagen til to faktorer:
- Den første er, at værdien af g, Jordens tyngdefelt svarende til tyngdekraftens acceleration, afhænger af breddegrad: maksimum ved polerne og minimum ved ækvator.
- Det andet er, at som vi sagde før, er densiteten af jorden ikke homogen. Der er steder, hvor det stiger, fordi klipperne er tættere, der er akkumulering af magma, eller der er meget jord på overfladen, som f.eks. Et bjerg.
Hvor tætheden er højere, g det er det også. Noter det g er en vektor, og det er derfor, det er angivet med fed skrift.
Jordens tyngdepotentiale
For at definere geoid er potentialet på grund af tyngdekraft nødvendigt, for hvilket tyngdefeltet skal defineres som tyngdekraften pr. Masseenhed.
Hvis en testmasse m er placeret i det nævnte felt, er den kraft, som jorden udøver på det, dets vægt P = mg, derfor er feltets størrelse:
Kraft / masse = P / m = g
Vi kender allerede dens middelværdi: 9,8 m / sto og hvis Jorden var sfærisk, ville den være rettet mod dens centrum. Tilsvarende ifølge Newtons lov om universel tyngdekraft:
P = Gm M / rto
Hvor M er jordens masse, og G er den universelle gravitationskonstant. Derefter størrelsen af tyngdefeltet g det er:
g = GM / rto
Det ligner meget et elektrostatisk felt, så der kan defineres et tyngdepotentiale, der er analogt med elektrostatisk:
V = -GM / r
Den konstante G er den universelle konstant for tyngdekraften. Nå kaldes overfladerne, hvor tyngdepotentialet altid har den samme værdi ækvipotentiale overflader Y g det er altid vinkelret på dem, som sagt før.
For denne specifikke klasse af potentiale er de ækvipotentiale overflader koncentriske kugler. Arbejdet, der kræves for at flytte en masse på dem, er nul, fordi kraften altid er vinkelret på enhver sti på potentialet.
Sidekomponent af tyngdeacceleration
Da jorden ikke er sfærisk, skal tyngdeaccelerationen have en lateral komponent gl på grund af centrifugalacceleration forårsaget af planetens rotationsbevægelse omkring sin akse.
Følgende figur viser denne komponent i grønt, hvis størrelse er:
gl = ωtotil
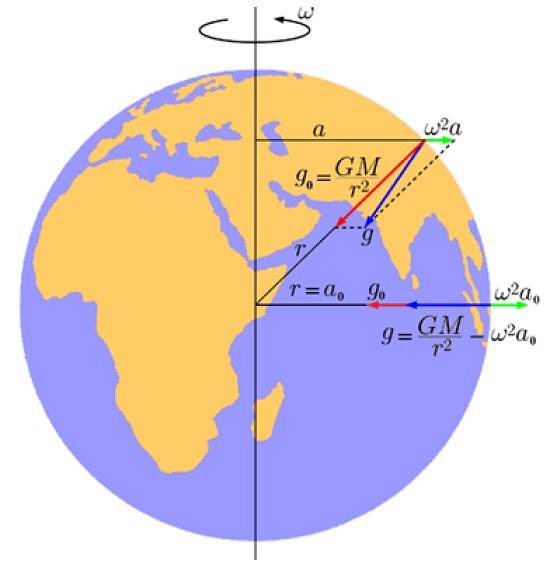
I denne ligning ω er jordens rotationshastighed og til er afstanden mellem punktet på jorden på en bestemt breddegrad og aksen.
Og i rødt er den komponent, der skyldes planetarisk tyngdekraftsattraktion:
geller = GM / rto
Som et resultat ved at tilføje vektor geller + gl, en resulterende acceleration opstår g (i blåt), som er den sande tyngdeacceleration på jorden (eller effektiv acceleration), og at som vi ser det ikke peger nøjagtigt mod centrum.
Desuden afhænger den laterale komponent af breddegrad: den er nul ved polerne, og tyngdefeltet er derfor maksimalt der. Ved ækvator modsætter den sig tyngdekraften og reducerer den effektive tyngdekraft, hvis størrelse forbliver:
g = GM / rto - ωtoR
Med R = Jordens ækvatoriale radius.
Det er nu forstået, at Jordens ækvipotentiale overflader ikke er sfæriske, men har en sådan form, at g altid være vinkelret på dem på alle punkter.
Forskelle mellem geoid og ellipsoid
Her er den anden faktor, der påvirker variationen i jordens tyngdefelt: de lokale variationer i tyngdekraften. Der er steder, hvor tyngdekraften øges, fordi der er mere masse, for eksempel på bakken i figur a).
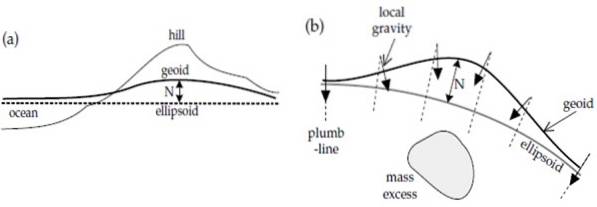
Eller der er en ophobning eller et overskud af masse under overfladen, som i b). I begge tilfælde er der en højde i geoiden, fordi jo større masse, jo større er tyngdefeltets intensitet..
På den anden side er tætheden over havet lavere, og som følge heraf synker geoiden, som vi ser til venstre for figur a), over havet..
Fra figur b) kan det også ses, at lokal tyngdekraft, angivet med pile, altid er vinkelret på geoidens overflade, som vi har sagt. Dette sker ikke altid med reference-ellipsoiden.
Geoidens bølger
Figuren angiver også med en tovejs pil forskellen i højden mellem geoiden og ellipsoiden, der kaldes bølget y betegnes som N. Positive bølger er relateret til overskydende masse og negative bølger til mangler.
Bølgerne overstiger næsten aldrig 200 m. Faktisk afhænger værdierne af, hvordan det havniveau, der fungerer som reference, vælges, da nogle lande vælger forskelligt i henhold til deres regionale karakteristika.
Fordele ved at repræsentere Jorden som en geoid
-På geoiden er det effektive potentiale, resultatet af potentialet på grund af tyngdekraften og centrifugalpotentialet, konstant.
-Tyngdekraften virker altid vinkelret på geoiden, og horisonten er altid tangential for den.
-Geoiden giver en reference til kortlægningsapplikationer med høj præcision.
-Ved hjælp af geoiden kan seismologer registrere dybden, hvor jordskælv opstår.
-GPS'ens placering afhænger af den geoid, der skal bruges som reference.
-Havoverfladen er også parallel med geoiden.
-Geoidens højder og nedstigninger indikerer overdreven eller massefejl, som er gravimetriske anomalier. Når en anomali opdages, og afhængigt af dens værdi, er det muligt at udlede den geologiske struktur af undergrunden i det mindste til visse dybder..
Dette er grundlaget for gravimetriske metoder inden for geofysik. En gravimetrisk anomali kan indikere ophobning af visse mineraler, strukturer begravet under jorden eller endda tomme rum. Saltkuplerne i undergrunden, der kan detekteres ved gravimetriske metoder, er i nogle tilfælde vejledende for tilstedeværelsen af olie.
Referencer
- AT. Euronews. Tyngdekraftens greb på jorden. Gendannet fra: youtube.com.
- GLÆDE. Geoid. Gendannet fra: youtube.com.
- Griem-Klee, S. Minedrift: gravimetri. Gendannet fra: geovirtual2.cl.
- Lowrie, W. 2007. Grundlæggende om geofysik. 2. plads Udgave. Cambridge University Press.
- NOAA. Hvad er geoid? Gendannet fra: geodesy.noaa.gov.
- Sheriff, R. 1990. Anvendt geofysik. 2. plads Udgave. Cambridge University Press.



Endnu ingen kommentarer