
Hvad er en icosagon? Egenskaber og egenskaber

EN icosagon eller isodecagon er en polygon, der har 20 sider. En polygon er en plan figur dannet af en endelig sekvens af linjesegmenter (mere end to), der omslutter en region af planet.
Hvert linjesegment kaldes en side, og skæringspunktet mellem hvert sidepar kaldes et toppunkt. I henhold til antallet af sider får polygonerne bestemte navne.

De mest almindelige er trekanten, firsidet, femkant og sekskant, som har henholdsvis 3, 4, 5 og 6 sider, men kan bygges med det antal sider, du ønsker.
Karakteristika for en icosagon
Nedenfor er nogle karakteristika ved polygoner og deres anvendelse i en ikosagon.
1- Klassifikation
En ikosagon, der er en polygon, kan klassificeres som regelmæssig og uregelmæssig, hvor ordet regelmæssigt henviser til det faktum, at alle sider har samme længde, og de indvendige vinkler alle måler de samme; ellers siges det, at icosagon (polygon) er uregelmæssig.
2- Isodecagon
Den almindelige icosagon kaldes også en regelmæssig isodecagon, for for at opnå en regelmæssig icosagon er det, du skal gøre, at halvere (opdele i to lige store dele) hver side af en regelmæssig decagon (10-sidet polygon).
3- Omkreds
For at beregne omkredsen "P" for en almindelig polygon ganges antallet af sider med længden af hver side.
I det særlige tilfælde af en icosagon er omkredsen lig med 20xL, hvor "L" er længden på hver side.
Hvis du f.eks. Har en almindelig icosagon med en 3 cm side, er dens omkreds lig med 20x3cm = 60cm.
Det er klart, at hvis isogonen er uregelmæssig, kan ovenstående formel ikke anvendes.
I dette tilfælde skal de 20 sider tilføjes separat for at opnå omkredsen, det vil sige omkredsen “P” er lig med ∑Li, med i = 1,2,…, 20.
4- Diagonaler
Antallet af diagonaler "D", som en polygon har, er lig med n (n-3) / 2, hvor n repræsenterer antallet af sider.
I tilfælde af en icosagon følger det, at den har D = 20x (17) / 2 = 170 diagonaler.
5- Summen af de interne vinkler
Der er en formel, der hjælper med at beregne summen af de indre vinkler af en regelmæssig polygon, som kan anvendes på en almindelig icosagon.
Formlen består i at trække 2 fra antallet af sider på polygonen og derefter multiplicere dette tal med 180º.
Sådan opnås denne formel er, at vi kan dele en polygon med n sider i n-2 trekanter, og ved at bruge det faktum, at summen af de indre vinkler i en trekant er 180 °, får vi formlen.
Følgende billede illustrerer formlen for en almindelig enegon (9-sidet polygon).
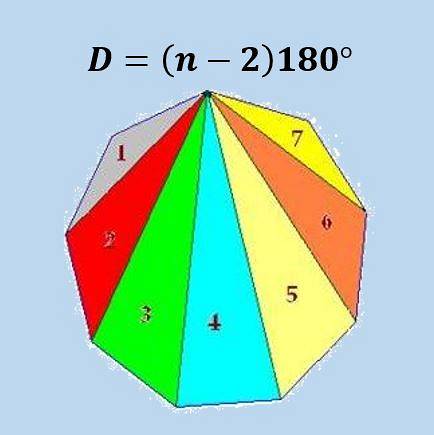
Ved hjælp af ovenstående formel opnås det, at summen af de indre vinkler for enhver icosagon er 18 × 180º = 3240º eller 18π.
6- Område
For at beregne arealet af en regelmæssig polygon er det meget nyttigt at kende begrebet apothem. Apotemet er en vinkelret linje, der går fra midten af den regelmæssige polygon til midtpunktet på en af dens sider.
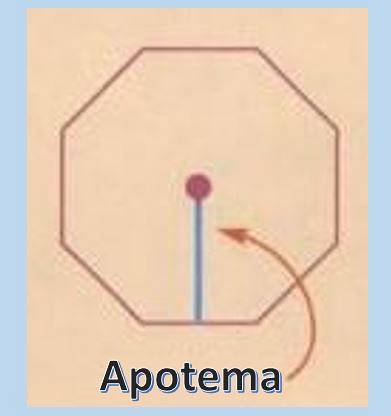
Når først apotemets længde er kendt, er arealet af en regelmæssig polygon A = Pxa / 2, hvor "P" repræsenterer omkredsen og "a" apotemet..
I tilfælde af en almindelig icosagon er dens areal A = 20xLxa / 2 = 10xLxa, hvor "L" er længden på hver side, og "a" er dens apotem.
På den anden side, hvis du har en uregelmæssig polygon med n sider, skal du beregne dens areal, opdele polygonen i n-2 kendte trekanter, derefter beregne arealet af hver af disse n-2 trekanter og til sidst tilføje alle disse områder.
Metoden beskrevet ovenfor er kendt som triangulering af en polygon.
Referencer
- C., E. Á. (2003). Geometrielementer: med adskillige øvelser og kompasgeometri. University of Medellin.
- Campos, F. J., Cerecedo, F. J., og Cerecedo, F. J. (2014). Matematik 2. Grupo Redaktionel Patria.
- Freed, K. (2007). Opdag polygoner. Benchmark Education Company.
- Hendrik, v. M. (2013). Generelle polygoner. Birkhäuser.
- IGER. (s.f.). Matematik Første semester Tacaná. IGER.
- jrgeometri. (2014). Polygoner. Lulu Press, Inc..
- Mathivet, V. (2017). Kunstig intelligens for udviklere: koncepter og implementering i Java. ENI-udgaver.
- Miller, Heeren & Hornsby. (2006). Matematik: ræsonnement og applikationer 10 / e (Tiende udgave). Pearson Uddannelse.
- Oroz, R. (1999). Ordbog over det spanske sprog. University Publishing House.
- Patiño, M. d. (2006). Matematik 5. Redaktionel Progreso.
- Rubió, M. d.-M. (1997). Formerne for byvækst. Univ. Politèc. fra Catalunya.


Endnu ingen kommentarer