
Bravais netværk koncept, egenskaber, eksempler, øvelser
Det Bravais-net De er sættet med fjorten tredimensionelle enhedsceller, hvor en krystalatomer kan placeres. Disse celler består af et tredimensionelt arrangement af punkter, der danner en grundlæggende struktur, der gentages periodisk i de tre rumlige retninger..
Oprindelsen af denne betegnelse for de grundlæggende krystallinske strukturer kommer fra 1850, da Auguste Bravais viste, at der kun er 14 mulige tredimensionelle basiske enhedsceller.

Sættet med 14 Bravais-netværk er opdelt i syv grupper eller strukturer i henhold til cellernes geometri, disse syv grupper er:
1- Kubisk
2- Tetragonal
3- Orthorhombisk
4- Trigonal-sekskantet
5- Monoklinik
6- Triklinik
7- Trigonal
Hver af disse strukturer definerer en enhedscelle, dette er den mindste del, der bevarer det geometriske arrangement af atomerne i krystallen..
Artikelindeks
- 1 Egenskaber ved Bravais-netværk
- 1.1 Kubiske netværk
- 2 Eksempler
- 2.1 - Jern
- 2.2 - Kobber
- 2.3 - Ædle perler
- 2.4 Topas
- 3 Løst øvelser
- 3.1 Øvelse 1
- 3.2 Øvelse 2
- 3.3 Øvelse 3
- 4 Referencer
Kendetegn ved Bravais-netværk
De fjorten Bravais-netværk, som nævnt ovenfor, er opdelt i syv grupper. Men hver af disse grupper har sine enhedsceller med sine karakteristiske parametre, som er:
1- Netværksparameteren (a, b, c)
2- Antal atomer pr. Celle
3- Forholdet mellem netværksparameter og atomradius
4- Koordineringsnummer
5- Pakningsfaktor
6- mellemrum
7- Gennem oversættelser langs vektorerne a, b, c gentages krystalstrukturen.
Kubiske netværk
Den består af det enkle kubiske eller kubiske netværk P, ansigt-centreret kubisk netværk eller kubisk netværk F og det kropscentrerede kubiske netværk eller kubiske netværk I.
Alle kubiske netværk har alle tre netværksparametre svarende til retningerne x, y, z med den samme værdi:
a = b = c
Kubisk netværk P
Det skal bemærkes, at atomer er repræsenteret af kugler, hvis centre er ved hjørnerne af den kubiske enhedscelle P.
I tilfælde af det kubiske gitter P antal atomer pr. celle er 1, fordi der ved hvert toppunkt kun en ottendedel af atomet er inde i enhedscellen, så 8 * ⅛ = 1.
Det koordinationsnummer angiver antallet af atomer, der er tætte naboer i krystalgitteret. For det kubiske gitter P er koordinationsnummeret 6.
Kubisk netværk I
I denne type netværk er der ud over atomer i terningens hjørner et atom i midten af terningen. Så antal atom pr. celle enhed i kubisk gitter P er 2 atomer.

Kubisk netværk F
Det er det kubiske gitter, der ud over atomerne i hjørnerne har et atom i midten af hver ternings ansigt. Det antal atomer pr. celle er 4, da hvert af de seks atomer i ansigtet har halvdelen inde i cellen, det vil sige 6 * ½ = 3 plus 8 * ⅛ = 1 i hjørnerne.

Sekskantet net
I dette tilfælde er enhedscellen et lige prisme med en sekskantet base. Sekskantede netværk har alle tre netværksparametre svarende til at opfylde følgende forhold:
a = b ≠ c
Vinklen mellem vektor a og b er 120º, som vist i figuren. Mens der mellem vektorer a og c samt mellem b og c dannes rette vinkler.

Det antal atomer pr. celle beregnes som følger:
- I hver af de to baser i det sekskantede prisme er der 6 atomer ved de seks hjørner. Hvert af disse atomer optager ⅙ af enhedscellen.
- I midten af hver af de 2 sekskantede baser er der 1 atom, der optager 1/2 enhedscelle.
- På de seks sideflader af det sekskantede prisme er der 3 atomer, der hver optager ⅔ af enhedscellen, og 3 atomer, der hver besætter ⅓ af enhedens cellevolumen.
(6 x ⅙) x 2 + ½ x 2 + ⅔ x 3 + ⅓ x 3 = 6
Forholdet mellem gitterparametrene a og b med atomradius R under den antagelse, at alle atomer har samme radius og er i kontakt er:
a / R = b / R = 2
Eksempler
Metaller er de vigtigste eksempler på krystallinske strukturer og også de enkleste, fordi de generelt kun består af en type atom. Men der er andre ikke-metalliske forbindelser, der også danner krystallinske strukturer, såsom diamant, kvarts og mange andre..
- Strygejernet
Jern har en enkelt kubisk enhedscelle med gitter eller kantparameter a = 0,297 nm. I 1 mm er der 3,48 x 10 ^ 6 enhedsceller.
- Kobber
Den har en ansigtscentreret kubisk krystallinsk struktur, der udelukkende består af kobberatomer..
- Dyrebare ædelstene
Ædle perler er krystallinske strukturer med stort set den samme forbindelse, men med små portioner urenheder, der ofte er ansvarlige for deres farve..
Diamant
Det består udelukkende af kulstof og indeholder ikke urenheder, hvorfor det er farveløst. Diamanten har kubisk krystalstruktur (isometrisk-hexoctahedral) og er det hårdeste kendte materiale.
Kvarts
Den består af silicaoxid, den er generelt farveløs eller hvid. Dens krystallinske struktur er trigonal-trapezohedral.
Rubin
Det er sammensat af aluminiumoxid med chromurenheder, der giver det sin karakteristiske røde farve. Form a sekskantet krystalgitter.
Safir
Det er også en krystal af aluminiumoxid, men med urenheder af titanium og jern, som er ansvarlige for dens blå farve i forskellige nuancer. Som rubinen har sekskantet struktur.
Jade
Ædelsten generelt grøn i farve, har monoklinisk struktur og er sammensat af jern-magnesium-calciumsilicat.
Topaz
Det er farveløst med en orthorhombisk struktur aluminiumfluorid-hydroxidsilicat.
Løst øvelser
Øvelse 1
Find forholdet mellem gitterparameteren og atomradius for et kubisk gitter F.
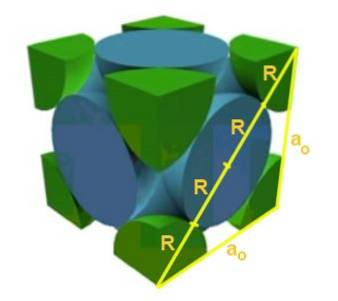
Opløsning: For det første antages det, at atomerne er repræsenteret som kugler hele radius R i "kontakt" med hinanden, som vist i figuren. En rigtig trekant dannes, hvor det er sandt, at:
(4 R) ^ 2 = a ^ 2 + a ^ 2 = 2 a ^ 2
Derfor er forholdet mellem kant og radius:
a / R = 4 / √2
Øvelse 2
Find forholdet mellem gitterparameteren og atomradius for et kubisk gitter I (kropscentreret).
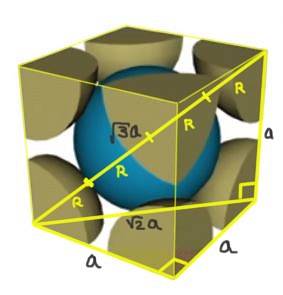
Opløsning: Atomer antages at være repræsenteret som kugler hele radius R i "kontakt" med hinanden, som vist i figuren.
To rigtige trekanter dannes, den ene af hypotenusen √2a og den anden af hypotenusen √3a som det kan bevises ved hjælp af Pythagoras sætning. Derfra følger det, at forholdet mellem gitterparameteren og atomradien for et kubisk gitter I (centreret i kroppen) er:
a / R = 4 / √3
Øvelse 3
Find pakningsfaktoren F for en enhedscelle med en kubisk struktur F (ansigt-centreret kubik), hvor atomerne har radius R og er i "kontakt".
Opløsning: Pakningsfaktoren F defineres som kvotienten mellem volumenet optaget af atomerne i enhedscellen og cellens volumen:
F = Vatomer / Vcelle
Som vist ovenfor er antallet af atomer pr. Enhedscelle i et ansigt-centreret kubisk gitter 4, så pakningsfaktoren vil være:
F = 4 [4πR ^ 3/3] / [a ^ 3] =…
… 4 [4πR ^ 3/3] / [4R / √2] ^ 3 = (√2) π / 6 = 0,74
Referencer
- Crystal Structures Academic Resource Center. [PDF]. Hentet den 24. maj 2018 fra: web.iit.edu
- Krystaller. Hentet den 26. maj 2018 fra: thoughtco.com
- Pressebøger. 10.6 Gitterstrukturer i krystallinske faste stoffer. Hentet den 26. maj 2018 fra: opentextbc.ca
- Ming. (2015, 30. juni). Typer Krystalstrukturer. Hentet den 26. maj 2018 fra: crystalvisions-film.com
- Helmenstine, Anne Marie, Ph.D. (31. januar 2018). Typer af
- Kittel Charles (2013) Solid State Physics, Condensed matter Physics (8. udgave). Wiley.
- KHI. (2007). Krystallinske strukturer. Hentet den 26. maj 2018 fra: folk.ntnu.no
- Wikipedia. Bravais gitter. Gendannet fra: en.wikipedia.com.



Endnu ingen kommentarer