
Simpsons regelformel, bevis, eksempler, øvelser
Det Simpsons hersker er en metode til på en omtrentlig måde at beregne bestemte integraler. Det er baseret på at opdele integrationsintervallet i et lige antal med lige store mellemrum.
De ekstreme værdier af to på hinanden følgende underintervaller definerer tre punkter, hvorved en parabel, hvis ligning er et andet graders polynom, passer.
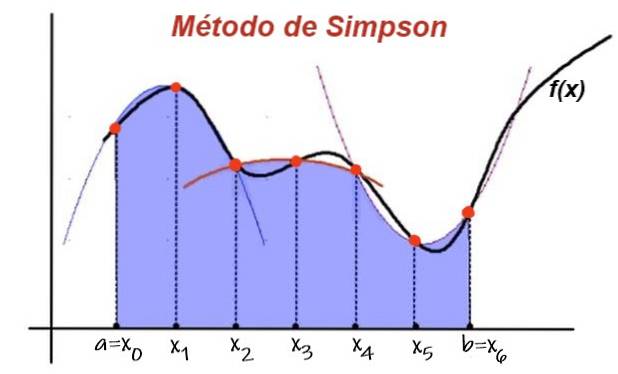
Derefter tilnærmes området under funktionens kurve i de to på hinanden følgende intervaller af området for interpolationspolynomet. Når vi tilføjer bidraget til området under parabolen af alle de efterfølgende delintervaller, har vi den omtrentlige værdi af integralen.
På den anden side, da integriteten af en parabel kan beregnes algebraisk nøjagtigt, er det muligt at finde en analytisk formel til den omtrentlige værdi af den bestemte integral. Det er kendt som Simpsons formel.
Fejlen i det således opnåede omtrentlige resultat falder, da antallet af underinddelinger n er større (hvor n er et lige antal).
Et udtryk vil blive givet nedenfor, der tillader estimering af den øvre grænse for fejlen i tilnærmelsen til integralet I, når der er foretaget en partition af n regelmæssige underintervaller af det samlede interval [a, b].
Artikelindeks
- 1 Formel
- 2 demo
- 2.1 Koefficienter for interpolationspolynomet
- 2.2 Beregning af den omtrentlige integral i [Xi, Xi + 2]
- 2.3 Omtrentlig beregning af integralen i [a, b]
- 2.4 Fejl i tilnærmelse
- 3 Arbejdede eksempler
- 3.1 - Eksempel 1
- 3.2 - Eksempel 2
- 3.3 - Eksempel 3
- 4 Foreslået øvelse
- 5 Referencer
Formel
Integrationsintervallet [a, b] er opdelt i n underintervaller, hvor n er et lige heltal. Bredden på hver underinddeling vil være:
h = (b - a) / n
På denne måde laves partitionen i intervallet [a, b]:
X0, X1, X2,…, Xn-1, Xn
Hvor X0 = a, X1 = X0 + h, X2 = X0 + 2h,…, Xn-1 = X0 + (n-1) h, Xn = X0 + nh = b.
Formlen, der gør det muligt at beregne den bestemte integral I i den kontinuerlige og fortrinsvis glatte funktion på intervallet [a, b] på en tilnærmet måde er:
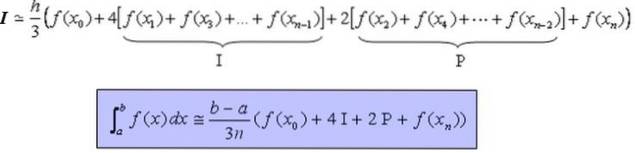
Demonstration
For at opnå Simpsons formel tilnærmes funktionen f (X) i hvert underinterval [Xi, Xi + 2] med en anden grad polynomial p (X) (parabel), der passerer gennem de tre punkter: [Xi, f (Xi)] ; [Xi + 1, f (Xi + 1)] og [Xi + 2, f (Xi + 2)].
Derefter beregner vi integralet af polynomet p (x) i [Xi, Xi + 2], der tilnærmer sig integralet af funktionen f (X) i det interval.
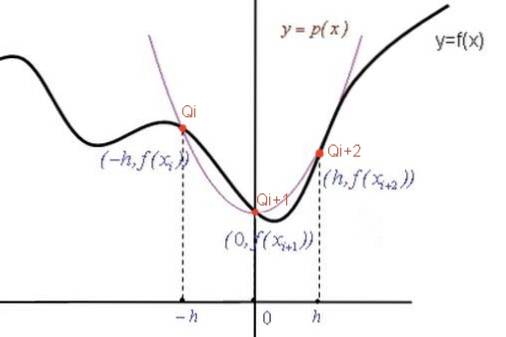
Koefficienter for interpolationspolynomet
Ligningen af parabolen p (X) har den generelle form: p (X) = A Xto + B X + C. Når parabolen passerer gennem de punkter, der er angivet med rødt (se figur), bestemmes koefficienterne A, B, C ud fra følgende ligningssystem:
A (-h)to - B h + C = f (Xi)
C = f (Xi + 1)
A (h)to + B h + C = f (Xi + 2)
Det kan ses, at koefficienten C bestemmes. For at bestemme koefficienten A tilføjer vi den første og tredje ligning, der opnås:
2 A hto + 2 C = f (Xi) + f (Xi + 2).
Derefter erstattes værdien af C, og A ryddes og efterlader:
A = [f (Xi) - 2 f (Xi + 1) + f (Xi + 2)] / (2 timerto)
For at bestemme koefficienten B trækkes den tredje ligning fra den første, og B løses, hvilket opnår:
B = [f (Xi + 2) - f (Xi)] = 2 timer.
Sammenfattende har andengrads polynom p (X), der passerer gennem punkterne Qi, Qi + 1 og Qi + 2 koefficienter:
A = [f (Xi) - 2 f (Xi + 1) + f (Xi + 2)] / (2 timerto)
B = [f (Xi + 2) - f (Xi)] = 2 timer
C = f (Xi + 1)
Beregning af den omtrentlige integral i [Xi, Xi + 2]
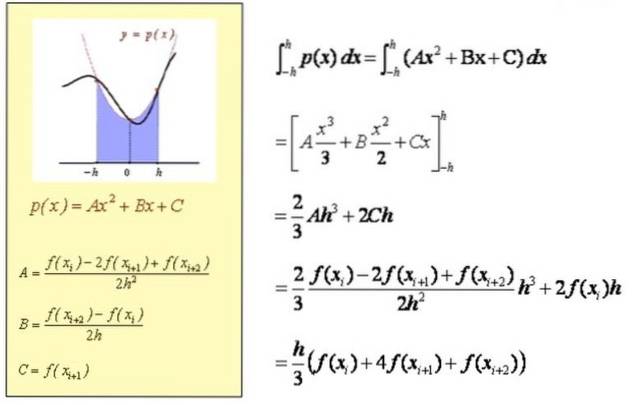
Omtrentlig beregning af integralen i [a, b]
Som allerede nævnt, på det samlede integrationsinterval [a, b] laves en partition X0, X1, X2,…, Xn-1, Xn med trin h = Xi + 1 - Xi = (b - a) / n , hvor n er et lige tal.
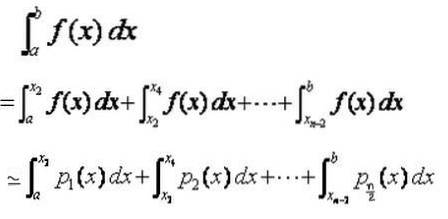
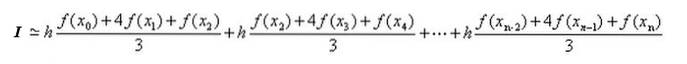
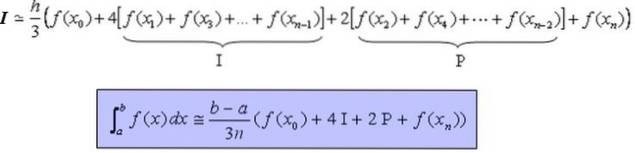
Tilnærmelsesfejl
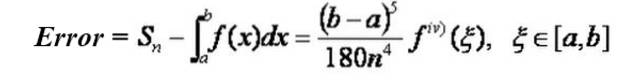
Bemærk, at fejlen falder med den fjerde effekt af antallet af underopdelinger i intervallet. For eksempel, hvis du går fra n underopdelinger til 2n, falder fejlen med en faktor 1/16.
Den øvre grænse for fejlen opnået gennem Simpson-tilnærmelsen kan opnås fra den samme formel, idet den fjerde derivat erstattes af den maksimale absolutte værdi af det fjerde derivat i intervallet [a, b].
Arbejdede eksempler
- Eksempel 1
Overvej funktionen funktionen f (X) = 1 / (1 + Xto).
Find den bestemte integral af funktionen f (X) i intervallet [-1, 1] ved hjælp af Simpsons metode med to underinddelinger (n = 2).
Opløsning
Vi tager n = 2. Grænserne for integration er a = -1 og b = -2, så partitionen ser sådan ud:
X0 = -1; X1 = 0 og X2 = +1.
Derfor har Simpsons formel følgende form:

Med n = 2 → xo = -1, x1 = 0; x2 = 1, derfor:

- Eksempel 2
Overvej funktionen f (X) = 1 / (1 + Xto).
Find den bestemte integral af funktionen f (X) i intervallet [-1, 1] ved hjælp af Simpsons formel med fire underinddelinger (n = 4).
Opløsning
Vi tager n = 4. Grænserne for integration er a = -1 og b = -2, så partitionen ser sådan ud:
X0 = -1; X1 = -1/2; X2 = 0; X3 = 1/2 og X4 = +1.
Simpsons formel er angivet således:
Integreret ≃ [(b -a) / (3 n)] [f (X0) + 4 I + 2 P + f (Xn)]
For det tilfælde, hvor det anvendes, er det som følger:
Integreret ≃ (1 - (1)) / (3⋅4)] [f (-1) + 4 [f (-½) + f (½)] + 2 [f (0)] + f (1)
Integreret ≃ (2/12) [½ + 4 (⅘ + ⅘) + 2⋅1 + ½] = (⅙) [47/5] = 47/30 = 1.5666
- Eksempel 3
Bestem den bestemte integral af de foregående eksempler nøjagtigt, og foretag en sammenligning af det nøjagtige resultat med dem, der opnås ved hjælp af Simpsons formel i eksemplerne 1a og 1b.
Opløsning
Den ubestemte integral af funktionen f (X) = 1 / (1 + Xto) er funktionen arctan (X).
Ved evaluering inden for grænserne for integration forbliver det:
Integral = arctan (1) - arctan (-1) = π / 4 - (-π / 4) = π / 2 = 1.5708
Hvis vi sammenligner resultatet af den nøjagtige løsning med den opnået ved Simpsons metode med n = 2 og n = 4, har vi:
For n = 2 er forskellen mellem den nøjagtige og den omtrentlige opløsning π / 2 - 5/3 = -0,0959, det vil sige en procentvis forskel på -0,06%.
Og for Simpson-tilnærmelsen med n = 4 er forskellen mellem den nøjagtige og den omtrentlige opløsning π / 2 - 47/30 = 0,0041, det vil sige en procentvis forskel på 0,003%.
Foreslået øvelse
Simpsons metode er velegnet til anvendelse i programmeringssprog og i computerapplikationer til matematiske beregninger. Det foreslås, at læseren, baseret på formlerne i denne artikel, skriver sin egen kode i sit yndlingsprogram.
Følgende figur viser en øvelse, hvor Simpsons formel er implementeret i Smath-studie, gratis software tilgængelig til operativsystemer Windows Y Android.

Referencer
- Casteleiro, J. M. 2002. Integral calculus (Illustreret udgave). Madrid: ESIC Editorial.
- UPV. Simpsons metode. Polytechnic universitet i Valencia. Gendannet fra: youtube.com
- Purcell, E. 2007. Calculus niende udgave. Prentice hall.
- Wikipedia. Simpsons regel. Gendannet fra: es.wikipedia.com
- Wikipedia. Lagrange polynomisk interpolation. Gendannet fra: es.wikipedia.com



Endnu ingen kommentarer