
Anden forklaring af ligevægtstilstand, eksempler, øvelser
Det anden ligevægtstilstand fastslår, at summen af drejningsmomenterne eller momentene, der produceres af alle kræfter, der virker på en krop, uanset hvilket punkt de beregnes, skal annulleres, så kroppen er i statisk eller dynamisk ligevægt.
Angiver drejningsmomentet eller kraftmomentet med det græske bogstav τ, matematisk udtrykkes det således:
∑ τ = 0

Det fede bogstav angiver momentets vektornatur, som skal annulleres i forhold til ethvert punkt valgt som omdrejningspunkt. Annullering af nettomomentet sikrer på denne måde, at objektet ikke begynder at rotere eller vælte..
Men hvis objektet allerede roterede tidligere, og nettomomentet pludselig forsvinder, fortsætter rotationen, men med konstant vinkelhastighed.
Den anden ligevægtstilstand bruges i forbindelse med den første betingelse, der siger, at summen af kræfterne på et legeme skal være nul, så det ikke oversættes, eller at hvis det gør det, er det med ensartet retlinjet bevægelse:
∑ F = 0
Begge betingelser gælder for udvidede kroppe, hvis dimensioner er målbare. Når et objekt antages at være en partikel, giver det ingen mening at tale om rotationer, og den første betingelse er tilstrækkelig til at garantere ligevægt.
Eksempler
Den anden ligevægtstilstand afsløres i utallige situationer:
Når du klatrer op ad stigen
Når vi understøtter en stige på gulvet og væggen, har vi brug for tilstrækkelig friktion, især på gulvet, for at sikre at stigen ikke glider. Hvis vi forsøger at klatre op på en stige understøttet på et fedtet, vådt eller glat gulv, er det ikke svært at forudse, at vi vil falde.
For at kunne bruge stigen med tillid er det nødvendigt, at den er i statisk balance under klatring, og når den er på det krævede trin.
Flytter et skab
Når du vil flytte et højt møbel som et skab eller et hvilket som helst stykke, hvis højde er større end bredden, er det praktisk at skubbe på et lavt punkt for at undgå at vælte, på denne måde er det mere sandsynligt, at møbler glider i stedet for at dreje og lægge sig.
Under sådanne omstændigheder er møblerne ikke nødvendigvis i ligevægt, da de kunne bevæge sig hurtigt, men i det mindste ville det ikke vælte.
Altaner
Altanerne, der stikker ud fra bygningerne, skal konstrueres, så selvom der er mange mennesker på toppen, vælter den ikke og kollapser.
Dielektrik i eksterne elektriske felter
Ved at placere et dielektrisk materiale i et eksternt elektrisk felt bevæger molekylerne sig og roterer, indtil de indtager en ligevægtsposition, hvilket skaber et elektrisk felt inde i materialet..
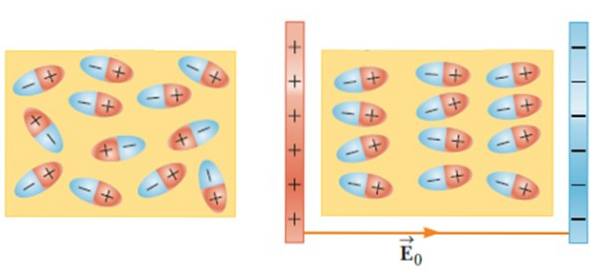
Denne effekt øger kapaciteten på en kondensator, når et materiale som glas, gummi, papir eller olie indsættes mellem rammerne..
Skilte og lamper
Det er almindeligt for mange lokale at hænge meddelelser på bygningens væg, så de er synlige for forbipasserende.
Plakaten holdes af en stang og et kabel, begge fastgjort til væggen med parenteser. De forskellige kræfter, der virker, skal sikre, at plakaten ikke falder, for hvilken de to ligevægtsbetingelser kommer i spil.
En reflektor kan også placeres på en sådan måde i en park, som i følgende figur:
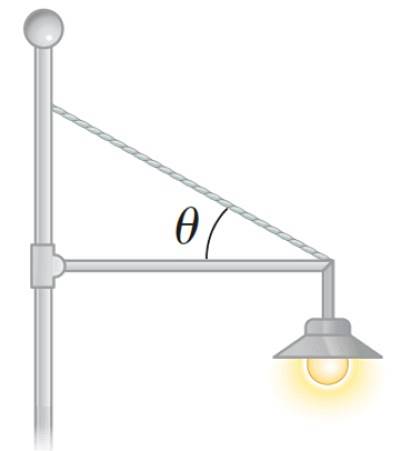
Sådan beregnes nettomomentet eller nettomomentet for en kraft?
Momentets kraft eller moment, betegnet med τ eller M i nogle tekster beregnes det altid med hensyn til et punkt, hvor rotationsaksen passerer.
Det er defineret som vektorproduktet mellem positionsvektoren r, der er rettet fra aksen til kraftens og kraftens påføringspunkt F:
τ = r × F
At være en vektor er det nødvendigt at udtrykke drejningsmomentet ved at give dets størrelse, retning og sans. Størrelsen er givet ved:
τ = rF.sen θ
Højre håndregel for vektorprodukt
Når problemet er i planet, er drejningsmomentets retning vinkelret på papiret eller skærmen, og retningen bestemmes af højre regel, hvor pegefingeren peger mod r, langfinger mod F og tommelfingeren peger ind eller ud af papiret.
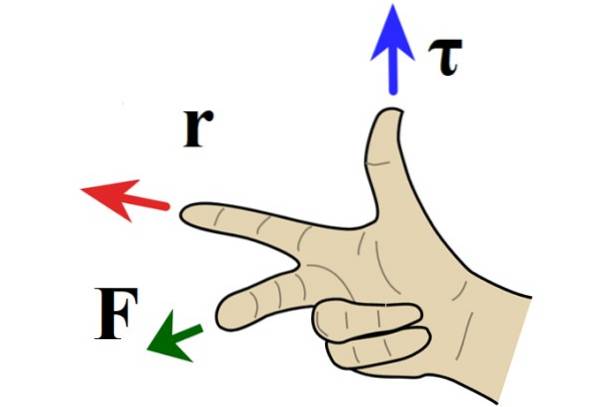
Når momentet peger ud af papiret, drejes drejningen mod uret og tildeles et positivt tegn ved konventionen. Hvis drejningsmomentet i stedet rettes mod indersiden af bladet, drejer det sig med uret og negativt..
For at finde nettomomentet vælges et praktisk punkt til beregningen, som kan være det, hvor den største mængde kræfter virker. I dette tilfælde er momentet for disse kræfter nul, da det har en positionsvektor r af størrelsesorden 0.
Du kan vælge ethvert punkt, der giver tilstrækkelig information til at løse det ukendte, der beder om, at problemet skal løses. Lad os se det mere detaljeret nedenfor.
Træning løst
Reflektoren i den følgende figur har en masse på 20 kg og understøttes af en tynd vandret stang med ubetydelig masse og længde L, der er hængslet til en stang. Kablet, også let, der hjælper med at støtte reflektoren danner en vinkel θ = 30º med stangen. Beregn:
a) Kabelspændingen
b) Størrelsen af kraften F, som stolpen udøver på stangen gennem hængslet.
Opløsning
Vi anvender den første ligevægtstilstand ∑ F = 0 til de kræfter, der er vist i diagrammet:
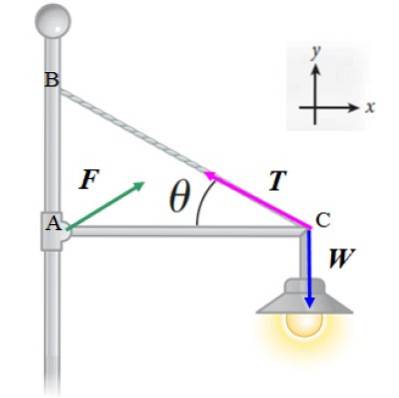
F + T + W = 0
Bemærk, at størrelsen og retningen af F er endnu ikke bestemt, men vi antager, at den har to komponenter: Fx og FY. På denne måde opnår vi to ligninger:
Fx -T. cos θ = 0
FY - W + T⋅ sin θ = 0
Lad os nu anvende den anden ligevægtstilstand ved at vælge punkt A, da vi ikke kender størrelsen på F heller ikke den af T. Ved at vælge dette punkt, vektoren rTIL er nul, derfor øjeblikket af F er nul og størrelsen af F vises ikke i ligningen:
-W⋅L + T⋅sen θ⋅L = 0
Derfor:
T.sen θ.L = W.L
T = W / sin θ = (20 kg x 9,8 m / sto) / Sin 30º = 392 N
Når vi kender størrelsen af T, kan vi løse komponenten Fx:
Fx = T⋅ cos θ = 392 cos 30º N = 339. 5 N
Og så komponent FY:
FY = W - T⋅ sin θ = (20 kg x 9,8 m / sto) - 392⋅sin 30º = 0
Så kan vi udtrykke F Så:
F = 339,5 N x
Det er derfor en vandret kraft. Dette skyldes, at vi mente, at stangen havde ubetydelig vægt.
Hvis punkt C var valgt til at beregne det resulterende øjeblik, var vektorerne rT Y rW er nul, derfor:
M = FogL = 0
Det konkluderes, at FY = 0. På denne måde:
- W + T⋅ sin θ = 0
T = W / sin θ
Hvilket er det samme resultat, der oprindeligt blev opnået ved valg af punkt A som det sted, hvor rotationsaksen passerer.
Temaer af interesse
Ligevægtsbetingelser.
Første ligevægtstilstand.
Referencer
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley.
- Figueroa, D. (2005). Serie: Fysik til videnskab og teknik. Bind 4. Partikelsystemer. Redigeret af Douglas Figueroa (USB).
- Giancoli, D. 2006. Fysik: Principper med applikationer. 6. Ed prentice hall.
- Sears, Zemansky. 2016. Universitetsfysik med moderne fysik. 14. Red. Bind 1.
- Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 1. 7. Ed. Cengage Learning.



Endnu ingen kommentarer