
Newtons anden lovansøgning, eksperimenter og øvelser
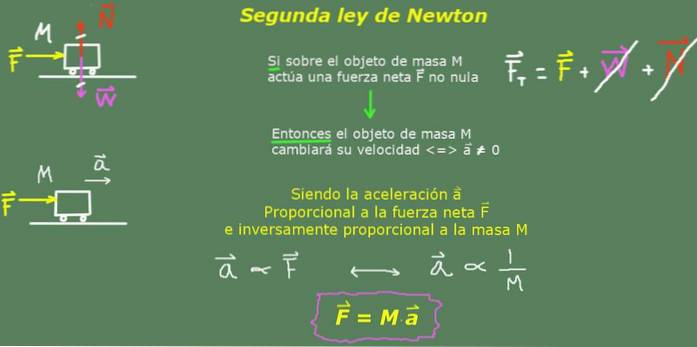
Det anden lov i Newton eller den grundlæggende dynamiklov fastslår, at hvis en genstand udsættes for en kraft eller et sæt kræfter, der ikke annullerer, vil genstanden accelereres i retning af den resulterende kraft, hvor denne acceleration er proportional med intensiteten af nettokraften og omvendt proportional med genstandens masse.
Ja F er nettokraften, M genstandens masse og til den acceleration, den opnår, så ville Newtons anden lov udtrykkes matematisk sådan: til = F / M eller på den mest sædvanlige måde F = M∙til
Artikelindeks
- 1 Forklaring og formler
- 2 Løst øvelser
- 2.1 Øvelse 1
- 2.2 Øvelse 2
- 3 Anvendelser af Newtons anden lov
- 3.1 Acceleration af en elevator
- 3.2 Mayonnaise-krukken
- 4 Eksperimenter for børn
- 4.1 Eksperiment 1
- 4.2 Eksperiment 2
- 5 Artikler af interesse
- 6 Referencer
Forklaring og formler
Som forklaret ovenfor er den sædvanlige måde at udtrykke den anden lov på med formlen:
F = M∙til
Både acceleration og kraft skal måles ud fra en inerti-referenceramme. Bemærk, at massen er en positiv størrelse, så accelerationen peger i samme retning som den resulterende kraft.
Bemærk også, at når den resulterende kraft er nul (F = 0) så vil accelerationen også være nul ( til = 0 ) så længe M> 0. Dette resultat stemmer helt overens med Newtons første lov eller inertilov.
Newtons første lov etablerer inertialreferencesystemer som dem, der bevæger sig med konstant hastighed i forhold til en fri partikel. I praksis og med henblik på de mest almindelige applikationer betragtes et referencesystem fastgjort til jorden eller ethvert andet, der bevæger sig med en konstant hastighed i forhold til det, som inertial..
Kraft er det matematiske udtryk for objektets interaktion med miljøet. Kraften kan være en konstant størrelse eller ændre sig med tiden, positionen og hastigheden på objektet..
Enheden i det internationale system (SI) for styrke er Newton (N). Massen i (SI) måles i (kg) og accelerationen i (m / s)to). Én Newton af kraft er den nødvendige kraft til at accelerere et objekt med en masse på 1 kg ved 1 m / sto .
Løst øvelser
Øvelse 1
Et objekt med masse m frigøres fra en bestemt højde, og en faldacceleration på 9,8 m / s² måles.
Det samme sker med et andet objekt med masse m 'og et andet med masse m "og et andet og et andet. Resultatet er altid tyngdeacceleration, der betegnes med g og er lig med 9,8 m / s². I disse eksperimenter er formen på genstand og dens masse er sådan, at kraften på grund af luftmodstand er ubetydelig.
Det bliver bedt om at finde en model for jordens tiltrækningskraft (kendt som vægt), der er i overensstemmelse med de eksperimentelle resultater..
Opløsning
Vi vælger et inertialreferencesystem (fast i forhold til jorden) med en positiv retning af den lodrette X-akse og nedad.
Den eneste kraft, der virker på masseobjektet m er jordens attraktion, den kraft kaldes vægten P, hvordan det peger ned er positivt.
Den acceleration, som masseobjektet erhverver m når det er frigivet, er det a = g , påpeget og positiv.
Vi foreslår Newtons anden lov
P = m a
Hvad vil være modellen for P, således at accelerationen forudsagt af den anden lov er g uanset værdien af m? : Det eneste alternativ er, at P = m g, når m> 0.
m g = m a hvorfra vi rydder: a = g
Vi konkluderer, at vægten, den kraft, hvormed Jorden tiltrækker et objekt, vil være genstandens masse ganget med tyngdeacceleration og dens retning er lodret og peget ned.
P = m∙g
Øvelse 2
En blok på 2 kg masse hviler på et helt fladt og vandret gulv. Hvis der påføres en kraft på 1 N, hvad er accelerationen af blokken, og hvilken hastighed den vil have efter 1 s.
Opløsning
Den første ting er at definere et inerti-koordinatsystem. Den ene er valgt med X-aksen på gulvet og Y-aksen vinkelret på den. Derefter laves et kraftdiagram, der placerer kræfterne på grund af interaktionerne mellem blokken og dens omgivelser.

Kraften N repræsenterer det normale, det er den lodrette opadgående kraft, som gulvoverfladen udøver på blokken M. Det er kendt, at N nøjagtigt afbalancerer P, fordi blokken ikke bevæger sig i lodret retning.
F er den vandrette kraft, der påføres blok M, der peger i den positive retning af X-aksen.
Nettokraften er summen af alle kræfterne på masseblokken M. Vi laver vektorsummen af F, P og N. Da P og N er lige og modsatte, annullerer de hinanden, og nettokraften er F.
Så den resulterende acceleration vil være kvotienten for nettokraften og massen:
a = F / M = 1 N / 2 kg = 0,5 m / s²
Da blokken starter fra hvile efter 1s, vil dens hastighed have ændret sig fra 0 m / s til 0,5 m / s .
Anvendelser af Newtons anden lov
Fremskynde en elevator
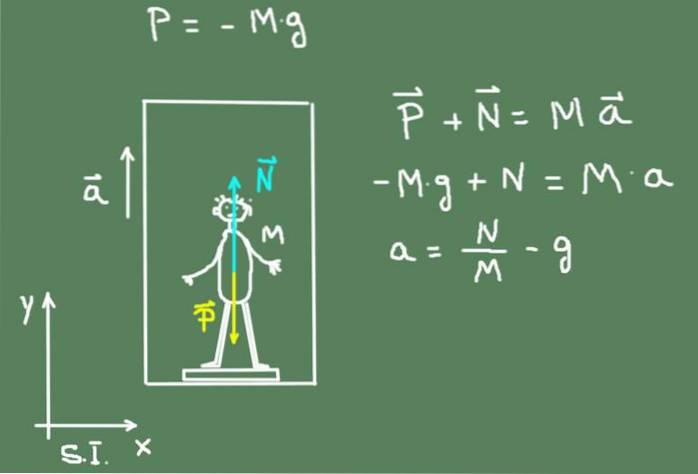
En dreng bruger en badeværelsesvægt til at måle sin vægt. Den værdi, du får, er 50 kg. Derefter tager drengen vægten til elevatoren i sin bygning, fordi han vil måle elevatorens acceleration. Resultaterne opnået ved opstart er:
- Vægten registrerer en vægt på 58 kg i 1,5 sek
- Mål derefter 50 kg igen.
Med disse data beregner du accelerationen af elevatoren og den hastighed, den opnår.
Opløsning
Vægten måler vægten i en enhed, der kaldes kilogram_styrke. Per definition er kilogramstyrken den kraft, hvormed planeten Jorden tiltrækker et objekt med en masse på 1 kg.
Når den eneste kraft, der virker på genstanden, er dens vægt, får den en acceleration på 9,8 m / s². Så 1 kg_f er lig med 9,8 N.
Vægten P af drengen er derefter 50 kg * 9,8 m / s² = 490 N
Under acceleration udøver skalaen en kraft N på drengen på 58 kg_f svarende til 58 kg * 9,8 m / s² = 568,4 N.
Elevatorens acceleration gives af:
a = N / M - g = 568,4 N / 50 kg - 9,8 m / s² = 1,57 m / s²
Hastigheden opnået af elevatoren efter 1,5 sek med acceleration på 1,57 m / s² er:
v = a * t = 1,57 m / s² * 1,5 s = 2,36 m / s = 8,5 Km / h
Følgende figur viser et diagram over de kræfter, der virker på drengen:
Mayonnaise-krukken
En dreng rækker sin bror mayonnaise til sin bror, som er i den anden ende af bordet. Til det kører det det på en sådan måde, at det får en hastighed på 3 m / s. Fra det øjeblik flasken blev frigivet, indtil den stoppede i den modsatte ende af bordet, var vandringen 1,5 m.
Bestem værdien af friktionskraften, som bordet udøver på flasken, idet du ved, at den har en masse på 0,45 kg.
Opløsning
Først skal vi bestemme bremseacceleration. Til dette vil vi bruge følgende forhold, der allerede er kendt fra den ensartede accelererede retlinede bevægelse:
Vf² = Vi² + 2 * a * d
hvor Vf er den endelige hastighed, Sav indledende hastighed, til acceleration og d forskydningen.
Accelerationen opnået fra det tidligere forhold er, hvor forskydningen af flasken er blevet betragtet som positiv.
a = (0 - 9 (m / s) ²) / (2 * 1,5 m) = -3 m / s²
Nettokraften på mayonnaise-krukken er friktionskraften, da den normale og vægten af krukken balancerer: Fnet = Fr.
Fr = m * a = 0,45 kg * (-3 m / s²) = -1,35 N = -0,14 kg-f
Eksperimenter for børn
Børn og voksne kan udføre enkle eksperimenter, der giver dem mulighed for at kontrollere, at Newtons anden lov virkelig fungerer i det virkelige liv. Her er to meget interessante:
Eksperiment 1
Et simpelt eksperiment kræver en badeværelsesvægt og en elevator. Tag et badeværelsesvægt ind i en elevator, og registrer de værdier, det markerer under opstart, nedstart og i den tid, du bevæger dig med konstant hastighed. Beregn elevatoraccelerationerne for hvert tilfælde.
Eksperiment 2
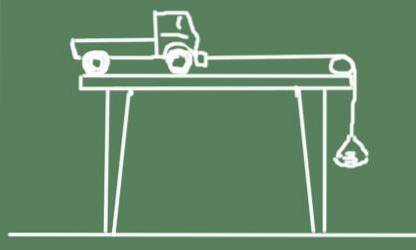
- Tag en legetøjsbil, der har hjulene smurt godt
- Fastgør et reb til enden.
- Ved kanten af bordet skal du tape en blyant eller en anden glat, cylindrisk genstand, hvor strengen passerer..
- I den anden ende af rebet skal du hænge en lille kurv, hvor du placerer nogle mønter eller noget, der tjener som en vægt..
Skemaet for eksperimentet er vist nedenfor:
- Smid vognen, og se, hvordan den bliver hurtigere.
- Forøg derefter vognens masse ved at placere mønter på den eller noget, der øger dens masse..
- Sig, om accelerationen stiger eller falder. Læg mere dej på vognen, se den accelerere og afslut.
Vognen efterlades derefter uden ekstra vægt og får lov til at accelerere. Der lægges derefter mere vægt på kurven for at øge den kraft, der påføres vognen..
- Sammenlign accelerationen med det foregående tilfælde, angiv, om den øges eller falder. Du kan gentage at tilføje mere vægt til kurven og observere accelerationen af vognen.
- Angiv, om den stiger eller falder.
- Analyser dine resultater, og sig om de er enige med Newtons anden lov eller ej.
Artikler af interesse
Eksempler på Newtons anden lov.
Newtons første lov.
Eksempler på Newtons anden lov.
Referencer
- Alonso M., Finn E. 1970. Fysikvolumen I: Mekanik. Interamerikansk Uddannelsesfond S.A. 156-163.
- Hewitt, P. 2012. Konceptuel fysik. Femte udgave. 41-46.
- Unge, Hugh. 2015. Universitetsfysik med moderne fysik. 14. udgave Pearson. 108-115.


Endnu ingen kommentarer