
Eksponentiel udjævningsmetode og eksempel
Det eksponentiel udjævning det er en måde at forudsige efterspørgslen efter en vare i en given periode. Denne metode estimerer, at efterspørgslen vil være lig med gennemsnittet af det historiske forbrug i en given periode, hvilket giver en større vægt eller vægt til de værdier, der er tættere på tiden. Derudover skal der for følgende prognoser tages hensyn til den eksisterende fejl i den aktuelle prognose.
Efterspørgselsprognoser er metoden til at projicere kundernes efterspørgsel efter et produkt eller en tjeneste. Denne proces er kontinuerlig, hvor ledere bruger historiske data til at beregne, hvad de forventer, at salgsefterspørgslen efter en vare eller tjenesteydelse skal være..
Oplysninger fra virksomhedens fortid bruges ved at føje dem til de økonomiske data på markedet for at se, om salget vil stige eller falde.
Resultaterne af efterspørgselsprognosen bruges til at sætte mål for salgsafdelingen og forsøge at være i tråd med virksomhedens mål.
Artikelindeks
- 1 Eksponentiel udjævningsmetode
- 1.1 Udjævning i prognosen
- 1.2 Vægtet glidende gennemsnit
- 1.3 Eksponentiel udjævning
- 2 Eksempel
- 3 Referencer
Eksponentiel udjævningsmetode
Udjævning er en meget almindelig statistisk proces. Udjævnede data findes ofte i forskellige former for hverdag. Hver gang et gennemsnit bruges til at beskrive noget, bruges et udjævnet tal.
Antag, at den varmeste vinter, der blev registreret, blev oplevet i år. For at kvantificere det starter vi med sættet af daglige temperaturdata for vinterperioden for hvert registrerede historiske år..
Dette genererer et antal tal med store "spring". Du har brug for et nummer, der fjerner alle disse spring fra dataene for lettere at kunne sammenligne en vinter med en anden.
Fjernelse af springet i data kaldes udjævning. I dette tilfælde kan et simpelt gennemsnit bruges til at opnå udjævning.
Udjævning i prognosen
Til forudsigelse af efterspørgsel bruges udjævning også til at eliminere variationer i historisk efterspørgsel. Dette muliggør bedre identifikation af efterspørgselsmønstre, som kan bruges til at estimere fremtidig efterspørgsel..
Variationer i efterspørgsel er det samme koncept som "spring" af temperaturdata. Den mest almindelige måde, hvorpå variationer i efterspørgselshistorikken fjernes, er at bruge et gennemsnit eller specifikt et glidende gennemsnit..
Det glidende gennemsnit bruger et foruddefineret antal perioder til at beregne gennemsnittet, og disse perioder bevæger sig, når tiden går..
For eksempel, hvis der anvendes et glidende gennemsnit på fire måneder, og i dag er 1. maj, vil den gennemsnitlige efterspørgsel for januar, februar, marts og april blive brugt. Den 1. juni vil kravet til februar, marts, april og maj blive brugt.
Vægtet glidende gennemsnit
Når du bruger et simpelt gennemsnit, anvendes den samme betydning for hver værdi i datasættet. Derfor repræsenterer hver måned 25% af det glidende gennemsnit i et glidende gennemsnit på fire måneder..
Ved at bruge efterspørgselshistorik til at projicere fremtidig efterspørgsel er det indlysende, at den seneste periode har større indflydelse på prognosen..
Du kan tilpasse beregningen af det glidende gennemsnit for at anvende forskellige "vægte" til hver periode for at opnå de ønskede resultater..
Disse vægte udtrykkes som procentdele. Det samlede antal af alle vægte i alle perioder skal være op til 100%.
Derfor, hvis du vil anvende 35% som vægten for den nærmeste periode i det fire måneders vægtede gennemsnit, kan du trække 35% fra 100%, hvilket efterlader 65% for at opdele mellem de tre resterende perioder.
For eksempel kan du ende med en vægtning på henholdsvis 15%, 20%, 30% og 35% i de fire måneder (15 + 20 + 30 + 35 = 100).
Eksponentiel udjævning
Kontrolindgangen til den eksponentielle udjævningsberegning er kendt som udjævningsfaktoren. Repræsenterer den vægt, der er anvendt på efterspørgslen i den seneste periode.
Hvis 35% bruges som den seneste periodevægt i den vægtede glidende gennemsnitberegning, kan du også vælge at bruge 35% som udjævningsfaktor i den eksponentielle udjævningsberegning..
Eksponentiel del
Forskellen i den eksponentielle udjævningsberegning er, at i stedet for at skulle finde ud af, hvor meget vægt der skal påføres for hver foregående periode, bruges udjævningsfaktoren til at gøre det automatisk..
Dette er den "eksponentielle" del. Hvis der anvendes 35% som udjævningsfaktor, vil efterspørgselsvægten for den seneste periode være 35%. Vægtningen af efterspørgslen fra den foregående periode til den seneste er 65% på 35%.
65% kommer fra at trække 35% fra 100%. Dette svarer til en vægtning på 22,75% for denne periode. Den næste seneste efterspørgsel vil være 65% fra 65% fra 35%, hvilket svarer til 14,79%.
Den foregående periode vægtes som 65% af 65% af 65% af 35%, svarende til 9,61%. Dette gøres for alle tidligere perioder op til den første periode.
Formel
Formlen til beregning af eksponentiel udjævning er som følger: (D * S) + (P * (1-S)), hvor,
D = seneste efterspørgsel i perioden.
S = udjævningsfaktor, repræsenteret i decimalform (35% ville være 0,35).
P = prognose for den seneste periode, resultat af udjævnningsberegningen for den foregående periode.
Hvis vi antager, at vi har en udjævningsfaktor på 0,35, ville vi have: (D * 0,35) + (P * 0,65).
Som du kan se, er de eneste datainput, der kræves, efterspørgslen og den seneste prognose for perioden..
Eksempel
Et forsikringsselskab har besluttet at udvide sit marked til den største by i landet med forsikring til køretøjer.
Som en første handling ønsker virksomheden at forudsige, hvor meget bilforsikring der vil blive købt af indbyggerne i denne by.
For at gøre dette bruger de som indledende data mængden af bilforsikring købt i en anden mindre by.
Efterspørgselsprognosen for periode 1 er 2.869 indgået køretøjsforsikring, men den faktiske efterspørgsel i den periode var 3.200.
Efter virksomhedens skøn tildeler den en udjævningsfaktor på 0,35. Den forventede efterspørgsel for den følgende periode er: P2 = (3200 * 0,35) + 2869 * (1-0,35) = 2984,85.
Den samme beregning blev foretaget for hele året med opnåelse af følgende sammenligningstabel mellem hvad der faktisk blev opnået og hvad der blev forventet for den måned.
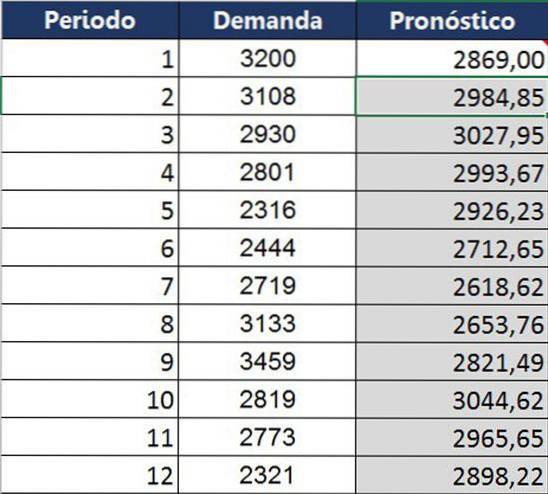
Sammenlignet med gennemsnitsteknikker kan eksponentiel udjævning forudsige tendensen bedre. Det er dog stadig kort, som vist i grafen:
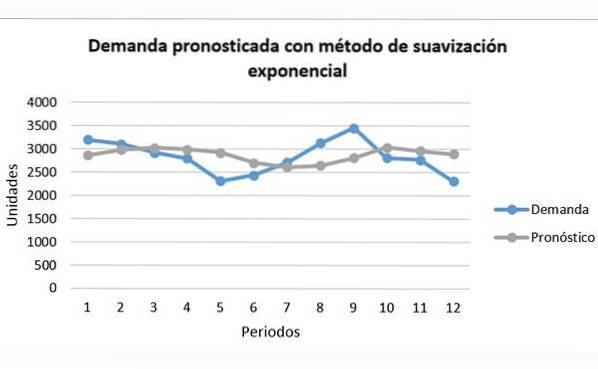
Det kan ses, hvordan den grå linje i prognosen kan være et godt stykke under eller over den blå efterspørgsel uden at være i stand til at følge den fuldt ud.
Referencer
- Wikipedia (2019). Eksponentiel udjævning. Hentet fra: es.wikipedia.org.
- Ingenio Empresa (2016). Sådan bruges simpel eksponentiel udjævning til at forudsige efterspørgsel. Hentet fra: ingenioempresa.com.
- Dave Piasecki (2019). Eksponentiel udjævning forklaret. Hentet fra: inventoryops.com.
- Undersøgelse (2019). Efterspørgselsteknikker: glidende gennemsnit og eksponentiel udjævning. Hentet fra: study.com.
- Cityu (2019). Eksponentielle udjævningsmetoder. Hentet fra: personal.cb.cityu.edu.hk.



Endnu ingen kommentarer