
Riemann sumhistorie, formler og egenskaber, øvelser
Det Riemann sum er navnet på den omtrentlige beregning af en bestemt integral ved hjælp af en diskret summering med et endeligt antal udtryk. En almindelig applikation er tilnærmelsen af funktionsområdet på en graf.
Det var den tyske matematiker Georg Friedrich Bernhard Riemann (1826-1866), der først tilbød en streng definition af integrationen af en funktion i et givet interval. Han gjorde det kendt i en artikel offentliggjort i 1854.
Riemann-summen er defineret på en funktion y = f (x), hvor x hører til det lukkede interval [a, b]. I dette interval laves en partition P af n-elementer:
P = x0= a, x1, xto,..., xn= b
Dette betyder, at intervallet er opdelt som følger:

xk-1 ≤ tk ≤ xk
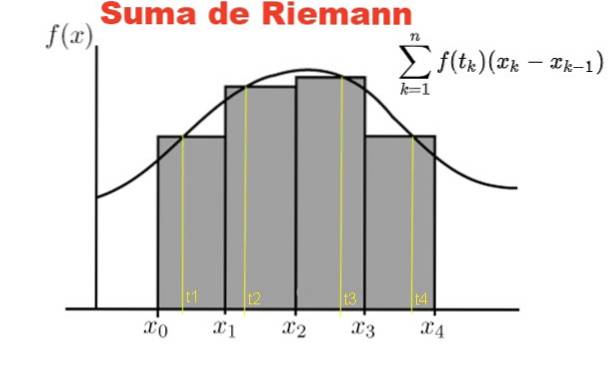
Figur 1 viser grafisk Riemann-summen af funktionen f på intervallet [x0, x4] på en skillevæg med fire underintervaller, de grå rektangler.
Summen repræsenterer det samlede areal af rektanglerne, og resultatet af denne sum tilnærmer sig numerisk arealet under kurven f mellem abscissen x = x0 y x = x4.
Selvfølgelig forbedres tilnærmelsen til området under kurven meget som antallet n skillevægge er større. På denne måde konvergerer summen til området under kurven, når tallet n af skillevægge har en tendens til uendelig.
Artikelindeks
- 1 Formler og egenskaber
- 1.1 Arealet under kurven
- 2 Løst øvelser
- 2.1 - Øvelse 1
- 2.2 - Øvelse 2
- 3 Referencer
Formler og egenskaber
Riemann-summen af funktionen f (x) på partitionen:
P = x0= a, x1, xto,..., xn= b
Defineret på intervallet [a, b], det er givet af:
S (P, f) = ∑k = 1n f (tk) (xk - xk-1)
Hvor Tk er en værdi på intervallet [xk, xk-1]. I Riemann-summen bruges normalt regelmæssige intervaller med bredde Δx = (b - a) / n, hvor a og b er minimums- og maksimumværdierne for abscissen, mens n er antallet af underinddelinger.
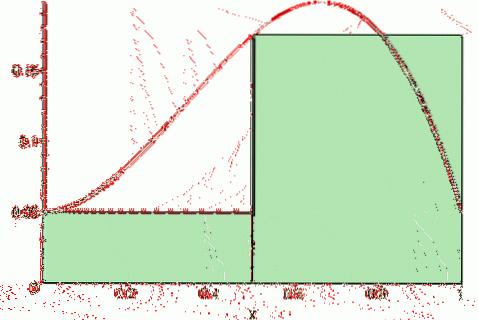
I så fald Riemann rigtige sum det er:
Sd (f, n) = [f (a + Δx) + f (a + 2Δx) +… + f (a + (n-1) Δx) + f (b)] * Δx
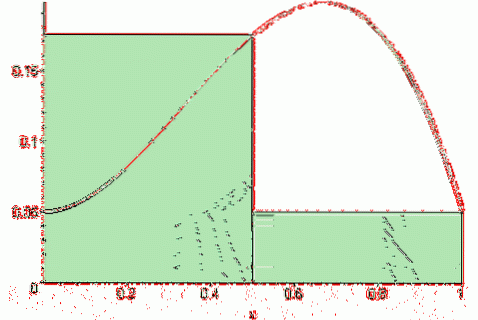
Mens Riemann efterlod summen udtrykkes som:
Hvis (f, n) = [f (a) + f (a + Δx) +… + f (a + (n-1) Δx)] * Δx
Endelig centrale Riemann sum det er:
Sc (f, n) = [f (a + Δx / 2) + f (a + 3Δx / 2) +… + f (b- Δx / 2)] * Δx
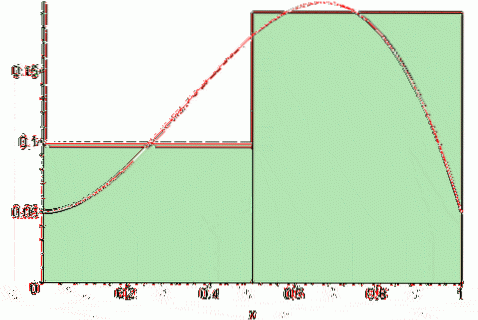
Afhængigt af hvor punktet t er placeretk i intervallet [xk, xk-1] Riemann-summen kan overvurdere eller undervurdere den nøjagtige værdi af området under kurven for funktionen y = f (x). Med andre ord kan rektanglerne stikke ud fra kurven eller være lidt under den..
Området under kurven
Hovedegenskaben for Riemann-summen, og hvorfra dens betydning stammer, er, at hvis antallet af underopdelinger har en tendens til uendelig, konvergerer resultatet af summen til funktionens bestemte integral:

Løst øvelser
- Øvelse 1
Beregn værdien af den bestemte integral mellem a = -2 til b = +2 for funktionen:
f (x) = xto
Brug en Riemann-sum. For at gøre dette skal du først finde summen for n regelmæssige partitioner af intervallet [a, b] og derefter tage den matematiske grænse for det tilfælde, at antallet af partitioner har tendens til uendelig.
Opløsning
Dette er trinene, du skal følge:
-Definér først intervallet for partitionerne som:
Δx = (b - a) / n.
-Derefter ser Riemann-summen fra højre svarende til funktionen f (x) sådan ud:


[-2 + (4i / n)]to = 4 - (16 i / n) + (4 / n)to jegto
-Og så erstattes det omhyggeligt i opsummeringen:

-Det næste trin er at adskille summeringerne og tage de konstante størrelser som en fælles faktor for hver sum. Det er nødvendigt at tage højde for, at indekset er i, derfor talene og vilkårene med n betragtes som konstante:

-Hver summering evalueres, da der for hver af dem er passende udtryk. For eksempel giver den første af summen n:



S (f, n) = 16 - 64 (n + 1) / 2n + 64 (n + 1) (2n + 1) / 6nto
-Endelig har vi, at integralen, som vi vil beregne, er:

= 16 - (64/2) + (64/3) = 16/3 = 5.333
Læseren kan kontrollere, at dette er det nøjagtige resultat, som kan opnås ved at løse den ubestemte integral og evaluere grænserne for integration ved Barrow's regel.
- Øvelse 2
Bestem ca. området under funktionen:
f (x) = (1 / √ (2π)) e(-xto/to)
Indtast x = -1 og x = + 1 ved hjælp af en central Riemann-sum med 10 partitioner. Sammenlign med det nøjagtige resultat, og estimer forskellen i procent.
Opløsning
Trin eller trin mellem to på hinanden følgende diskrete værdier er:
Ax = (1 - (-1) / 10 = 0,2
Så partitionen P, som rektanglerne er defineret på, ser sådan ud:
P = -1,0; -0,8; -0,6; -0,4; -0,2; 0,0; 0,2; 0,4; 0,6; 0,8; 1.0
Men da det, der ønskes, er den centrale sum, vil funktionen f (x) blive evalueret ved midtpunkterne for underintervallerne, dvs. i sættet:
T = -0,9; -0,7; -0,5; -0,3; -0,1; 0,1; 0,3; 0,5; 0,7; 0.9.
Den (centrale) Riemann-sum ser sådan ud:
S = f (-0,9) * 0,2 + f (-0,7) * 0,2 + f (-0,5) * 0,2 +… + f (0,7) * 0,2 + f (0,9) * 0,2
Da funktionen f er symmetrisk, er det muligt at reducere summen til kun 5 termer, og resultatet ganges med to:
S = 2 * 0,2 * f (0,1) + f (0,3) + f (0,5) + f (0,7) + f (0,9)
S = 2 * 0,2 * 0,397+ 0,381+ 0,352+ 0,312+ 0,266 = 0,683
Funktionen givet i dette eksempel er ingen ringere end den velkendte Gaussiske klokke (normaliseret, med gennemsnit lig med nul og standardafvigelse en). Arealet under kurven i intervallet [-1,1] for denne funktion er kendt for at være 0,6827.

Dette betyder, at den omtrentlige løsning med kun 10 udtryk matcher den nøjagtige løsning med tre decimaler. Den procentvise fejl mellem den omtrentlige og den nøjagtige integral er 0,07%.
Referencer
- Casteleiro, J. M. og Gómez-Álvarez, R. P. (2002). Integral calculus (Illustreret udgave). Madrid: ESIC Editorial.
- Unican. Historien om begrebet integral. Gendannet fra: repositorio.unican.es
- UIS. Summer Riemann. Gendannet fra: matematicas.uis.edu.co
- Wikipedia. Riemann sum. Gendannet fra: es.wikipedia.com
- Wikipedia. Riemann integration. Gendannet fra: es.wikipedia.com



Endnu ingen kommentarer