
Teleskopisk opsummering, hvordan det løses og øvelser løses

Det summering teleskopisk er en gren af operationer med nummerserier. Adresserer opsummeringen af elementer fra en indledende værdi til "n" af udtryk, hvis argument overholder et af følgende mønstre:
(Fx - Fx + 1); (Fx + 1 - Fx)
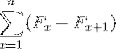
Som også:
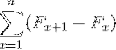

De repræsenterer en sammenfatning af elementer, der, når de er udviklet, udsættes for annulleringer af modsatte vilkår. Gør det muligt at definere følgende ligestilling for teleskopiske summeringer:
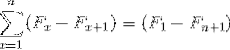
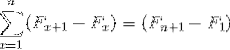
Navnet stammer fra forholdet til udseendet af et klassisk teleskop, som kunne foldes og foldes ud, især ændre dens dimension. På samme måde kan teleskopiske summeringer, som er uendelige i naturen, opsummeres i det forenklede udtryk:
F1 - Fn + 1
Artikelindeks
- 1 demo
- 2 Sådan løses?
- 2.1 Nedbrydning i enkle fraktioner
- 3 Historie
- 4 Øvelser
- 4.1 Øvelse 1
- 4.2 Øvelse 2
- 5 Referencer
Demonstration
Når man udvikler en opsummering af vilkår, er eliminering af faktorer ret åbenlyst. Hvor for hver af tilfældene, vises modsatte elementer i den næste iteration.
Den første sag (Fx - Fx + 1), da processen fungerer på en homolog måde for (Fx + 1-Fx).
Udvikling af de første 3 værdier 1, 2, 3 observeres tendensen til forenkling
x1 (F1 - F1 + 1) = F1 - Fto
xto (Fto - F2 + 1) = Fto - F3
x3 (F3 - F3 + 1) = F3 - F4
Hvor, når summen af de beskrevne elementer udtrykkes:
x1 + xto + x3 = F1 - Fto + Fto - F3 + F3 - F4
Det bemærkes, at F-termerneto og F3 de beskrives sammen med deres modsætninger, hvilket gør deres forenkling uundgåelig. På samme måde bemærkes det, at udtrykkene F1 og F4 forblive.
Hvis summen blev foretaget fra x = 1 til x = 3, betyder det, at elementet F4 svarer til det generiske udtryk Fn + 1.
Således demonstrerer lighed:
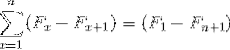
Hvordan løses det?
Formålet med de teleskopiske summeringer er at lette arbejdet, så det ikke er nødvendigt at udvikle et uendeligt antal udtryk eller at forenkle en kæde af tilføjelser, der er for lange.
For sin opløsning vil det kun være nødvendigt at evaluere F-vilkårene1 og Fn + 1. Disse enkle udskiftninger udgør det endelige resultat af summeringen.
De samlede vilkår udtrykkes ikke, de bliver kun nødvendige for demonstration af resultatet, men ikke for den normale beregningsproces.
Det vigtige er at bemærke konvergensen i nummerserierne. Sommetider vil summeringsargumentet ikke blive udtrykt teleskopisk. I disse tilfælde er implementeringen af alternative factoring-metoder meget almindelig..
Den karakteristiske faktoriseringsmetode i teleskopiske tilføjelser er den for enkle fraktioner. Dette sker, når en original fraktion nedbrydes i en sum af flere fraktioner, hvor det teleskopiske mønster (Fx - Fx + 1) eller (Fx + 1 - Fx).
Nedbrydning i enkle fraktioner
For at verificere konvergensen af de numeriske serier er det meget almindeligt at transformere rationelle udtryk med metoden med enkle brøker. Målet er at modellere plottet i form af en teleskopisk opsummering..
For eksempel repræsenterer følgende ligestilling en nedbrydning i enkle fraktioner:
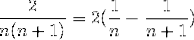
Når man udvikler nummerserier og anvender de tilsvarende egenskaber, tager udtrykket følgende form:
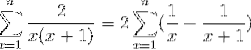
Hvor den teleskopiske form (Fx - Fx + 1).
Proceduren er ret intuitiv og består i at finde tællerens værdier, der uden at bryde ligestillingen tillader at adskille de produkter, der er i nævneren. Ligningerne, der opstår ved bestemmelsen af disse værdier, hæves i henhold til sammenligninger mellem begge sider af ligestillingen.
Denne procedure observeres trin for trin i udviklingen af øvelse 2.
Historie
Det er ret usikkert at være i stand til at definere det historiske øjeblik, hvor de teleskopiske summeringer blev præsenteret. Imidlertid begynder dens implementering at blive set i det syttende århundrede i undersøgelser af numeriske serier udført af Leibniz og Huygens..
Begge matematikere, der udforsker summeringerne af trekantede tal, begynder at lægge mærke til tendenser i konvergensen af visse serier af successive elementer. Men endnu mere interessant er starten på modelleringen af disse udtryk i elementer, der ikke nødvendigvis følger hinanden.
Faktisk anvendte udtrykket tidligere for at henvise til enkle brøker:
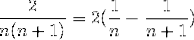
Det blev introduceret af Huygens og fangede straks Leibniz 'opmærksomhed. Hvem over tid kunne observere konvergensen til værdien 2. Uden at vide det implementerede han det teleskopiske summeringsformat.
Uddannelse
Øvelse 1
Definer til hvilket udtryk følgende sum konvergerer:
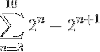
Ved manuel udvikling af summen observeres følgende mønster:
(to3 - to4) + (24 - to5) + (25 - to6) ... (to10 - toelleve)
Hvor faktorerne fra 24 op til 210 De præsenterer positive og negative dele, hvilket gør deres annullering tydelig. Så er de eneste faktorer, der ikke vil blive forenklet, de første "23”Og den sidste“ 2elleve".
På denne måde opnås følgende ved implementering af det teleskopiske summationskriterium:
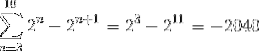
Øvelse 2
Transformér argumentet til en teleskopisk summation og definer konvergensen af serien:
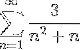
Som angivet i udsagnet vil den første ting at gøre være at nedbrydes i enkle brøker for at gentage argumentet og udtrykke det på en teleskopisk måde..
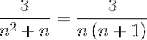
Du skal finde to fraktioner, hvis nævnere er henholdsvis "n" og "n + 1", hvor metoden, der anvendes nedenfor, skal opnå værdierne på tælleren, der svarer til ligestillingen.
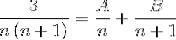
Vi fortsætter med at definere værdierne for A og B. Først skal du tilføje fraktionerne.
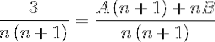
Derefter forenkles nævnerne, og der oprettes en lineær ligning.
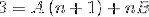
I det næste trin betjenes udtrykket til højre, indtil der opnås et mønster, der kan sammenlignes med “3” til venstre..
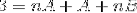
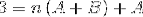
For at definere ligningerne, der skal bruges, skal resultaterne fra begge sider af ligestillingen sammenlignes. Det vil sige, at ingen værdier for variablen n observeres på venstre side, på denne måde skal A + B være lig med nul.
A + B = 0; A = -B
På den anden side skal den konstante værdi A være lig med den konstante værdi 3.
A = 3
Derfor.
A = 3 og B = -3
Når tællerværdierne for de enkle fraktioner allerede er defineret, ændres summeringen.
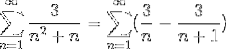
Hvor den generiske form for teleskopisk summering allerede er opnået. Teleskopserien er udviklet.
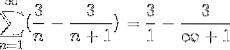
Hvor resultatet, når man deler med et meget stort antal, bliver tættere og tættere på nul ved at observere konvergensen af serien til værdien 3.
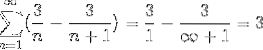
Denne type serier kunne ikke løses på nogen anden måde på grund af det uendelige antal iterationer, der definerer problemet. Imidlertid rammer denne metode sammen med mange andre grenen af studiet af numeriske serier, hvis mål er at bestemme konvergensværdierne eller definere divergensen mellem nævnte serier..
Referencer
- Infinitesimal calculus lektioner. Manuel Franco, Manuel Franco Nicolás, Francisco Martínez González, Roque Molina Legaz. EDITUM, 1994.
- Integral calculus: sekvenser og række funktioner. Antonio Rivera Figueroa. Grupo Editorial Patria, 21. okt. 2014.
- Et kursus i beregning og reel analyse. Sudhir R. Ghorpade, Balmohan V. Limaye. Springer Science & Business Media, 5. juni. 2006.
- Uendelig serie. Tomlinson Fort. The Clarendon Press, 1930.
- Elementer i teorien om uendelige processer. Lloyd Leroy Smail. McGraw-Hill Book Company, Incorporated, 1923.



Endnu ingen kommentarer