
Bolzanos sætning Forklaring, anvendelser og øvelser
Det Bolzano's sætning fastslår, at hvis en funktion er kontinuerlig på alle punkter i et lukket interval [a, b], og det er sandt, at billedet af "a" og "b" (under funktionen) har modsatte tegn, så vil der være mindst en punkt "C" i det åbne interval (a, b) på en sådan måde, at den funktion, der evalueres i "c", vil være lig med 0.
Denne sætning blev forkyndt af filosofen, teologen og matematikeren Bernard Bolzano i 1850. Denne videnskabsmand, født i det nuværende Tjekkiet, var en af de første matematikere i historien, der formelt beviste egenskaberne ved kontinuerlige funktioner..
Artikelindeks
- 1 Forklaring
- 2 demo
- 3 Hvad er det til??
- 4 Løst øvelser
- 4.1 Øvelse 1
- 4.2 Øvelse 2
- 5 Referencer
Forklaring
Bolzanos sætning er også kendt som sætningen mellemliggende værdier, som hjælper med at bestemme specifikke værdier, især nuller, af visse reelle funktioner i en reel variabel.
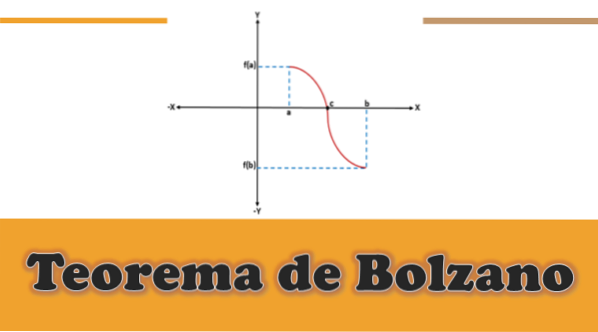
I en given funktion fortsætter f (x) -det vil sige, at f (a) og f (b) er forbundet med en kurve-, hvor f (a) er under x-aksen (den er negativ), og f ( b) over x-aksen (den er positiv) eller omvendt, grafisk vil der være et afskæringspunkt på x-aksen, der repræsenterer en mellemværdi "c", som vil være mellem "a" og “B”, og værdien af f (c) er lig med 0.
Ved grafisk at analysere Bolzanos sætning kan det ses, at for hver kontinuerlig funktion f defineret i et interval [a, b], hvor f (a)*f (b) er mindre end 0, vil der være mindst en rod "c" for denne funktion inden for intervallet (a, b).
Denne sætning fastlægger ikke antallet af punkter i det åbne interval, det siger kun, at der er mindst 1 punkt.
Demonstration
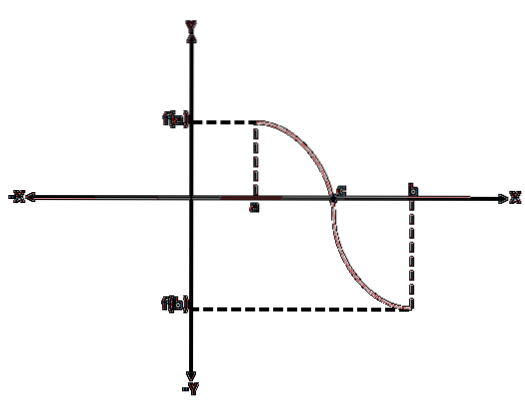
For at bevise Bolzanos sætning antages det uden tab af generalitet, at f (a) < 0 y f(b) > 0; der kan således være mange værdier mellem "a" og "b", for hvilke f (x) = 0, men det er kun nødvendigt at vise, at der er en.
Vi begynder med at evaluere f ved midtpunktet (a + b) / 2. Hvis f ((a + b) / 2) = 0, slutter beviset her; ellers er f ((a + b) / 2) positiv eller negativ.
En af halvdelene af intervallet [a, b] vælges, således at tegnene på den funktion, der evalueres i ekstremiteterne, er forskellige. Dette nye interval vil være [a1, b1].
Hvis f vurderet ved midtpunktet af [a1, b1] nu ikke er nul, udføres den samme operation som før; det vil sige, at den ene halvdel af dette interval vælges, der opfylder betingelsen for tegnene. Lad dette nye interval være [a2, b2].
Hvis du fortsætter med denne proces, har du to sekvenser an og bn, således at:
an stiger og bn falder:
a ≤ a1 ≤ a2 ≤… ≤ an ≤…. ≤…. ≤ bn ≤…. ≤ b2 ≤ b1 ≤ b.
Hvis længden af hvert interval [ai, bi] beregnes, har vi:
b1-al = (b-a) / 2.
b2-a2 = (b-a) / 2².
... .
bn-an = (b-a) / 2 ^ n.
Derfor er grænsen som n tendens til uendelig (bn-an) lig med 0.
Brug af, at an øges og begrænses, og bn falder og begrænses, vi har, at der findes en værdi "c", således at:
a ≤ a1 ≤ a2 ≤… ≤ an ≤… .≤ c ≤…. ≤ bn ≤…. ≤ b2 ≤ b1 ≤ b.
Grænsen for et er "c" og grænsen for bn er også "c". Givet ethvert δ> 0 er der derfor altid et "n", således at intervallet [an, bn] er indeholdt i intervallet (c-δ, c + δ).
Nu skal det vises, at f (c) = 0.
Hvis f (c)> 0, så da f er kontinuerlig, findes der en ε> 0 sådan at f er positiv over hele intervallet (c-ε, c + ε). Som nævnt ovenfor er der imidlertid en værdi "n", således at f ændrer tegn i [an, bn] og derudover er [an, bn] indeholdt i (c-ε, c + ε), hvilket hvad der er en modsigelse.
Hvis f (c) < 0, entonces como f es continua, existe un ε >0 således, at f er negativ i hele intervallet (c-e, c + e); men der er en værdi "n" sådan at f ændrer tegn i [an, bn]. Det viser sig, at [an, bn] er indeholdt i (c-ε, c + ε), hvilket også er en modsigelse.
Derfor er f (c) = 0, og det er det, vi ønskede at vise.
Hvad er det for?
Fra sin grafiske fortolkning bruges Bolzanos sætning til at finde rødder eller nuller i en kontinuerlig funktion gennem gennemskæring (tilnærmelse), som er en inkrementel søgemetode, der altid deler intervallerne med 2.
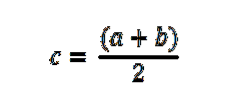
Derefter tages et interval [a, c] eller [c, b], hvor tegnændringen sker, og processen gentages, indtil intervallet er mindre og mindre for at komme tættere på den ønskede værdi; det vil sige til den værdi, som funktionen gør 0.
Sammenfattende: For at anvende Bolzano's sætning og således finde rødderne, begrænse nuller til en funktion eller give en løsning på en ligning, udføres følgende trin:
- Det verificeres, hvis f er en kontinuerlig funktion på intervallet [a, b].
- Hvis intervallet ikke er angivet, skal man finde, hvor funktionen er kontinuerlig.
- Det verificeres, hvis ekstremerne i intervallet giver modsatte tegn, når de vurderes ved f.
- Hvis der ikke opnås modsatte tegn, skal intervallet deles i to underintervaller ved hjælp af midtpunktet.
- Evaluer funktionen ved midtpunktet og kontroller, at Bolzano-hypotesen er opfyldt, hvor f (a) * f (b) < 0.
- Afhængigt af tegnet (positivt eller negativt) på den fundne værdi gentages processen med et nyt underinterval, indtil den førnævnte hypotese er opfyldt..
Løst øvelser
Øvelse 1
Bestem om funktionen f (x) = xto - 2, har mindst en reel løsning i intervallet [1,2].
Opløsning
Vi har funktionen f (x) = xto - 2. Da det er polynom, betyder det, at det er kontinuerligt i ethvert interval.
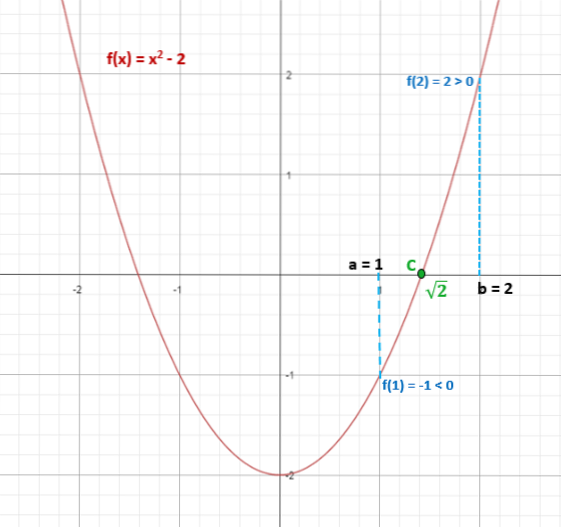
Det bliver bedt om at afgøre, om det har en reel løsning i intervallet [1, 2], så nu er det kun nødvendigt at erstatte ekstremerne af intervallet i funktionen for at kende tegnet på disse og at vide, om de opfylder betingelsen at være anderledes:
f (x) = xto - to
f (1) = 1to - 2 = -1 (negativ)
f (2) = 2to - 2 = 2 (positiv)
Derfor tegn på f (1) ≠ tegn f (2).
Dette sikrer, at der er mindst et punkt "c", der hører til intervallet [1,2], hvor f (c) = 0.
I dette tilfælde kan værdien af "c" let beregnes som følger:
xto - 2 = 0
x = ± √2.
Således hører √2 ≈ 1,4 til intervallet [1,2] og opfylder at f (√2) = 0.
Øvelse 2
Vis, at ligningen x5 + x + 1 = 0 har mindst en reel løsning.
Opløsning
Lad os først bemærke, at f (x) = x5 + x + 1 er en polynomfunktion, hvilket betyder, at den er kontinuerlig på alle reelle tal.
I dette tilfælde er der ikke givet noget interval, så værdier skal vælges intuitivt, helst tæt på 0, for at evaluere funktionen og finde tegnændringerne:
Hvis du bruger intervallet [0, 1], skal du:
f (x) = x5 + x + 1.
f (0) = 05 + 0 + 1 = 1> 0.
f (1) = 15 + 1 + 1 = 3> 0.
Da der ikke er nogen tegnændring, gentages processen med et andet interval.
Hvis du bruger intervallet [-1, 0], skal du:
f (x) = x5 + x + 1.
f (-1) = (-1)5 + (-1) + 1 = -1 < 0.
f (0) = 05 + 0 + 1 = 1> 0.
I dette interval er der et tegnændring: tegn på f (-1) ≠ tegn på f (0), hvilket betyder, at funktionen f (x) = x5 + x + 1 har mindst en reel rod "c" i intervallet [-1, 0], således at f (c) = 0. Med andre ord er det sandt, at x5 + x + 1 = 0 har en reel løsning i intervallet [-1,0].
Referencer
- Bronshtein I, S. K. (1988). Matematikhåndbog for ingeniører og studerende ... Redaktionel MIR.
- George, A. (1994). Matematik og sind. Oxford University Press.
- Ilín V, P. E. (1991). Matematisk analyse. I tre bind ...
- Jesús Gómez, F. G. (2003). Gymnasiale lærere. Bind II. GAL.
- Mateos, M. L. (2013). Grundlæggende egenskaber ved analyse i R. Editores, 20. dec.
- Piskunov, N. (1980). Differentiel og integreret beregning ...
- Sydsaeter K, H. P. (2005). Matematik til økonomisk analyse. Felix Varela.
- William H. Barker, R. H. (s.f.). Kontinuerlig symmetri: Fra Euclid til Klein. American Mathematical Soc.



Endnu ingen kommentarer