
Chebyshovs sætning, hvad det er, applikationer og eksempler
Det Chebyshovs sætning (eller Chebyshovs ulighed) er et af de vigtigste klassiske resultater af sandsynlighedsteori. Det giver mulighed for at estimere sandsynligheden for en begivenhed, der er beskrevet i form af en tilfældig variabel X, ved at give os en grænse, der ikke afhænger af fordelingen af den tilfældige variabel, men af variansen af X.
Teoremet er opkaldt efter den russiske matematiker Pafnuty Chebyshov (som også er skrevet som Chebychev eller Tchebycheff), der til trods for ikke at være den første til at sætte sætningen, var den første til at give et bevis i 1867.

Denne ulighed, eller dem, der på grund af deres egenskaber kaldes Chebyshovs ulighed, bruges hovedsageligt til at tilnærme sandsynligheder ved at beregne grænser.
Artikelindeks
- 1 Hvad gør?
- 2 Anvendelser og eksempler
- 2.1 Begrænsning af sandsynligheder
- 2.2 Bevis for grænsesætninger
- 2.3 Prøvestørrelse
- 3 uligheder af Chebyshov-typen
- 4 Referencer
Hvad består det af?
I studiet af sandsynlighedsteori sker det, at hvis fordelingsfunktionen for en tilfældig variabel X er kendt, kan dens forventede værdi eller matematiske forventning E (X) - og dens varians Var (X) beregnes, så længe sådanne beløb eksisterer . Imidlertid er det omvendte ikke nødvendigvis sandt..
Det vil sige, at kende E (X) og Var (X) er det ikke nødvendigvis muligt at opnå fordelingsfunktionen af X, og derfor er størrelser såsom P (| X |> k) for nogle k> 0 meget vanskelige at opnå. Men takket være Chebyshovs ulighed er det muligt at estimere sandsynligheden for den tilfældige variabel.
Chebyshovs sætning fortæller os, at hvis vi har en tilfældig variabel X over et prøveområde S med en sandsynlighedsfunktion p, og hvis k> 0, så:
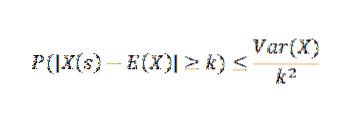
Anvendelser og eksempler
Blandt de mange anvendelser af Chebyshovs sætning kan følgende nævnes:
Begrænsende sandsynligheder
Dette er den mest almindelige anvendelse og bruges til at give en øvre grænse for P (| X-E (X) | ≥k) hvor k> 0 kun med variansen og forventningen af den tilfældige variabel X uden at kende sandsynlighedsfunktionen.
Eksempel 1
Antag, at antallet af produkter, der fremstilles i en virksomhed i løbet af en uge, er en tilfældig variabel med et gennemsnit på 50.
Hvis det vides, at variansen i en produktionsuge er lig med 25, hvad kan vi så sige om sandsynligheden for, at produktionen i denne uge adskiller sig med mere end 10 fra gennemsnittet?
Opløsning
Anvendelse af Chebyshovs ulighed har vi:
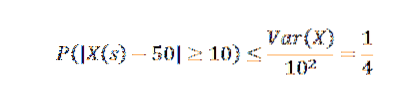
Ud fra dette kan vi opnå, at sandsynligheden for, at antallet af artikler i produktionsugen overstiger gennemsnittet med mere end 10 højst er 1/4.
Bevis for grænsesætninger
Chebyshovs ulighed spiller en vigtig rolle for at bevise de vigtigste grænsesætninger. Som et eksempel har vi følgende:
Svag lov af stort antal
Denne lov fastslår, at givet en sekvens X1, X2,…, Xn, ... af uafhængige tilfældige variabler med den samme gennemsnitlige fordeling E (Xi) = μ og varians Var (X) = σto, og en kendt middelprøve af:
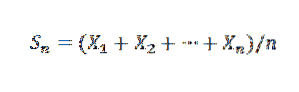
Så for k> 0 har vi:
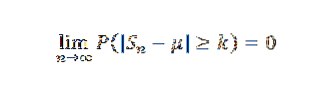
Eller tilsvarende:
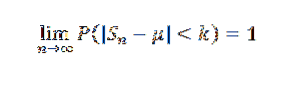
Demonstration
Lad os først bemærke følgende:
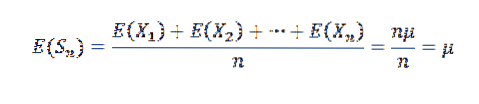
Da X1, X2,…, Xn er uafhængige, følger det således:
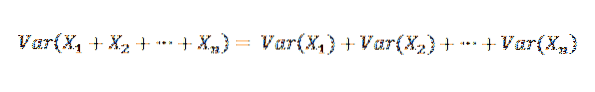
Derfor er det muligt at angive følgende:
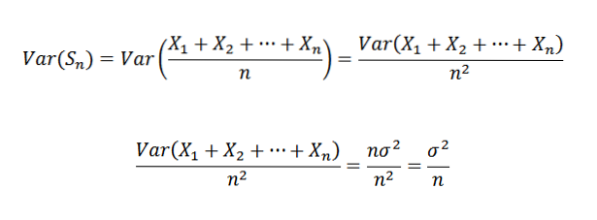
Derefter har vi ved hjælp af Chebyshovs sætning:
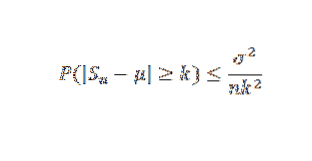
Endelig skyldes sætningen, at grænsen til højre er nul, når n har tendens til uendelig.
Det skal bemærkes, at denne test kun blev udført for det tilfælde, hvor variationen af Xi findes; det vil sige, det afviger ikke. Således observerer vi, at sætningen altid er sand, hvis E (Xi) findes.
Chebyshov begrænse sætning
Hvis X1, X2,…, Xn,… er en sekvens af uafhængige tilfældige variabler, så der er noget C< infinito, tal que Var(Xn) ≤ C para todo n natural, entonces para cualquier k>0:
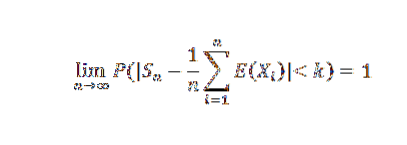
Demonstration
Da afvigelsessekvensen er ensartet afgrænset, har vi den Var (Sn) ≤ C / n, for alle naturlige n. Men vi ved det:
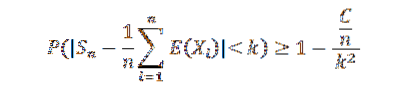
At få n til at være uendelig, følgende resultater:
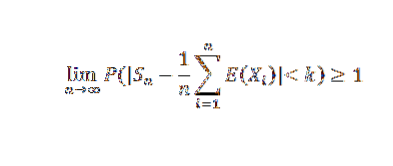
Da en sandsynlighed ikke kan overstige værdien 1, opnås det ønskede resultat. Som en konsekvens af denne sætning kunne vi nævne Bernoullis særlige tilfælde.
Hvis et eksperiment gentages n gange uafhængigt med to mulige resultater (fiasko og succes), hvor p er sandsynligheden for succes i hvert eksperiment, og X er den tilfældige variabel, der repræsenterer antallet af opnåede succeser, så for hver k> 0 har du til:
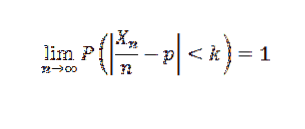
Prøvestørrelse
Med hensyn til variansen giver Chebyshov-uligheden os mulighed for at finde en stikprøvestørrelse n, der er tilstrækkelig til at garantere, at sandsynligheden for, at | Sn-μ |> = k forekommer, er så lille som ønsket, hvilket giver os mulighed for at have en tilnærmelse til gennemsnit.
Lad X1, X2, ... Xn være en prøve af uafhængige tilfældige variabler af størrelse n og antag, at E (Xi) = μ og dens varians σto. Så ved Chebyshovs ulighed har vi:
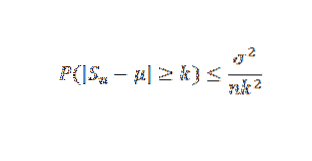
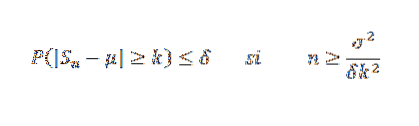
Eksempel
Antag at X1, X2, ... Xn er en prøve af uafhængige tilfældige variabler med Bernoulli-fordeling, således at de tager værdien 1 med sandsynligheden p = 0,5.
Hvad skal være størrelsen på prøven for at kunne garantere, at sandsynligheden for, at forskellen mellem det aritmetiske gennemsnit Sn og dens forventede værdi (overstiger mere end 0,1), er mindre end eller lig med 0., 01?
Opløsning
Vi har, at E (X) = μ = p = 0,5, og at Var (X) = σto= p (1-p) = 0,25. Ved Chebyshovs ulighed har vi for enhver k> 0:
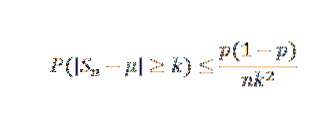
Når vi nu tager k = 0,1 og δ = 0,01, har vi:
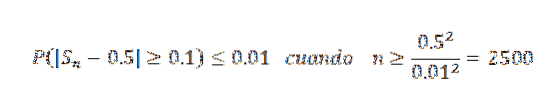
På denne måde konkluderes det, at der er behov for en stikprøvestørrelse på mindst 2500 for at garantere, at sandsynligheden for begivenheden | Sn - 0,5 |> = 0,1 er mindre end 0,01.
Uligheder af Chebyshov-typen
Der er flere uligheder relateret til Chebyshovs ulighed. En af de mest kendte er ulighederne i Markov:
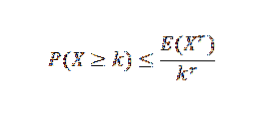
I dette udtryk er X en ikke-negativ tilfældig variabel med k, r> 0.
Markov-uligheden kan tage forskellige former. Lad f.eks. Y være en ikke-negativ tilfældig variabel (så P (Y> = 0) = 1) og antag at E (Y) = μ findes. Antag også, at (E (Y))r= μr eksisterer for noget heltal r> 1. Derefter:
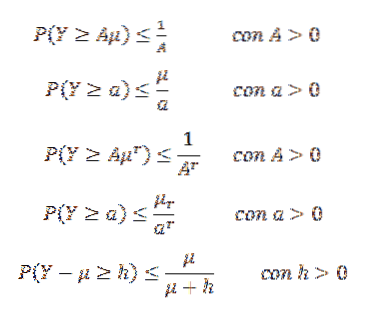
En anden ulighed er Gaussian, som fortæller os, at givet en unimodal tilfældig variabel X med mode på nul, så for k> 0,
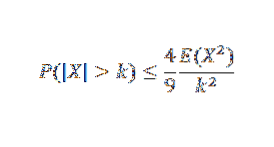
Referencer
- Kai Lai Chung. Elementær sandsynlighedsteori med stokastiske processer. Springer-Verlag New York Inc.
- Kenneth.H. Rosen. Diskret matematik og dens anvendelser. S.A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Paul L. Meyer. Sandsynlighed og statistiske anvendelser. S.A. MEXICAN ALHAMBRA.
- Seymour Lipschutz Ph.D. 2000 Løste problemer med diskret matematik. McGRAW-HILL.
- Seymour Lipschutz Ph.D. Problemer med teori og sandsynlighed. McGRAW-HILL.



Endnu ingen kommentarer