
Nortons sætningsbeskrivelse, applikationer, eksempler og øvelser
Det Nortons sætning, som anvendes på elektriske kredsløb, fastslår, at et lineært kredsløb med to terminaler a og b kan erstattes af et helt ækvivalent, der består af en strømkilde kaldet IIkke forbundet parallelt med en modstand RIkke.
Nævnte nuværende IIkke jeg hørteN Det er den, der ville flyde mellem punkt a og b, hvis de var kortsluttede. Modstanden RN er den tilsvarende modstand mellem terminalerne, når alle uafhængige kilder slukker. Alt sagt er skitseret i figur 1.

Den sorte boks i figuren indeholder det lineære kredsløb, der skal erstattes af dets Norton-ækvivalent. Et lineært kredsløb er et, hvor input og output har en lineær afhængighed, såsom forholdet mellem spændingen V og jævnstrømmen I et ohmsk element: V = I.R.
Dette udtryk svarer til Ohms lov, hvor R er modstanden, som også kan være en impedans, hvis det er et vekselstrømskredsløb.
Nortons sætning blev udviklet af elektroingeniøren og opfinderen Edward L. Norton (1898-1983), der arbejdede i lang tid for Bell Labs..
Artikelindeks
- 1 Anvendelser af Nortons sætning
- 1.1 Forholdet mellem Norton og Thevenin sætninger
- 2 Eksempel
- 3 Øvelse løst
- 4 Referencer
Anvendelser af Nortons sætning
Når du har meget komplicerede netværk med mange modstande eller impedanser, og du vil beregne spændingen mellem et hvilket som helst af dem eller den strøm, der strømmer gennem det, forenkler Nortons sætning beregningerne, da netværket som vi har set kan erstattes af et mindre og mere håndterbart kredsløb.
På denne måde er Nortons sætning meget vigtig, når man designer kredsløb med flere elementer såvel som at studere deres svar..
Forholdet mellem Norton og Thevenin sætninger
Nortons sætning er den dobbelte af Thevenins sætning, hvilket betyder, at de er ækvivalente. Thevenins sætning indikerer, at den sorte boks i figur 1 kan erstattes af en spændingskilde i serie med en modstand, kaldet Thevenin-modstanden RTh. Dette udtrykkes i følgende figur:
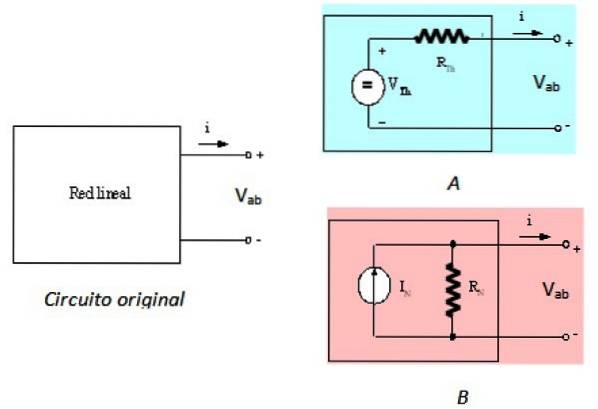
Kredsløbet til venstre er det originale kredsløb, det lineære netværk i den sorte boks, kredsløb A øverst til højre er Thevenin-ækvivalenten og kredsløbet B det er Norton-ækvivalenten, som beskrevet. Set fra terminal a og b er de tre kredsløb ækvivalente.
Bemærk nu, at:
-I det originale kredsløb er spændingen mellem terminalerne V.ab.
-Vab = VTh i kredsløbet TIL
-Endelig Vab = JegN.RN i kredsløbet B
Hvis terminal a og b kortsluttes i alle tre kredsløb, skal det være tilfreds med, at spændingen og strømmen mellem disse punkter skal være den samme for alle tre, da de er ækvivalente. Derefter:
-I det originale kredsløb er strømmen i.
-For kredsløb A er strømmen i = V.Th / RTh, ifølge Ohms lov.
-Endelig i kredsløb B er strømmen IN
Derfor konkluderes det, at modstandene i Norton og Thevenin har samme værdi, og at strømmen er givet af:
jeg = jegN = VTh / RTh = VTh / RN
Eksempel
For at anvende Nortons sætning korrekt følges følgende trin:
-Isoler fra netværket den sektion af kredsløbet, som Norton-ækvivalenten skal findes for.
-I det resterende kredsløb skal du angive terminalerne a og b.
-Erstat spændingskilderne for kortslutninger og de aktuelle kilder for åbne kredsløb for at finde den ækvivalente modstand mellem klemmerne a og b. Dette er RN.
-Sæt alle kilder tilbage til deres originale positioner, kortslutningsterminaler a og b, og find den strøm, der flyder mellem dem. Dette er jegN.
-Tegn Norton-ækvivalent kredsløb i henhold til det, der er angivet i figur 1. Både den aktuelle kilde og den tilsvarende modstand er parallelle.
Du kan også anvende Thevenins sætning for at finde RTh, som vi allerede ved er lig med RN, så ved Ohms lov kan du finde migN og fortsæt med at tegne det resulterende kredsløb.
Og lad os nu se et eksempel:
Find Norton-ækvivalenten mellem punkterne A og B i følgende kredsløb:
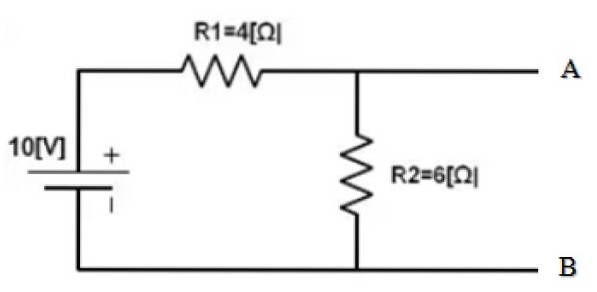
Den del af kredsløbet, hvis ækvivalent skal findes, er allerede isoleret. Og punkt A og B er tydeligt bestemt. Det følgende er at kortslutte 10 V-kilden og finde den tilsvarende modstand af det opnåede kredsløb:
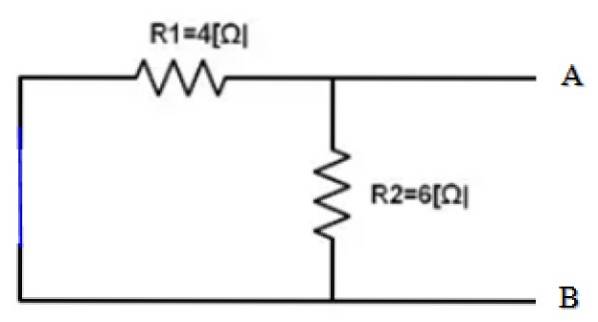
Udsigt fra terminal A og B, begge modstande R1 og Rto er parallelle, derfor:
1 / Rækv = 1 / R12 = (1/4) + (1/6) Ω-1 = 5/12 Ω-1 → Rækv = 12/5 Ω = 2,4 Ω
Derefter returneres kilden til sit sted, og punkterne A og B kortsluttes for at finde den strøm, der cirkulerer der, dette vil være jegN. I det tilfælde:
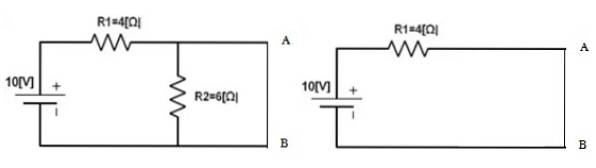
jegN = 10 V / 4 Ω = 2,5 A
Norton-ækvivalent
Endelig tegnes Norton-ækvivalenten med de fundne værdier:
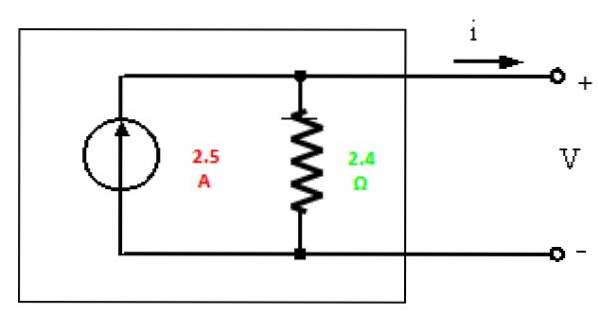
Træning løst
I kredsløbet i følgende figur:
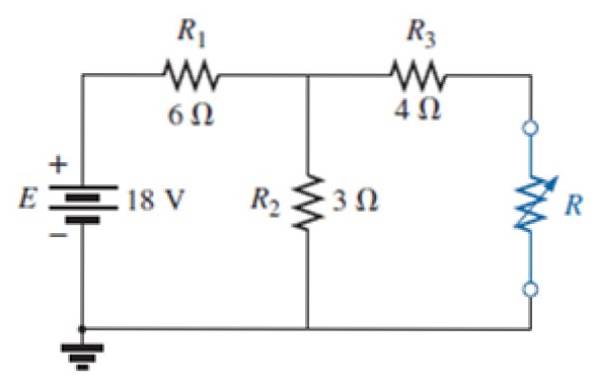
a) Find Norton-ækvivalent kredsløb for det eksterne netværk til den blå modstand.
b) Find også Thévenin-ækvivalenten.
Løsning til
Efter ovenstående trin skal kilden kortsluttes:
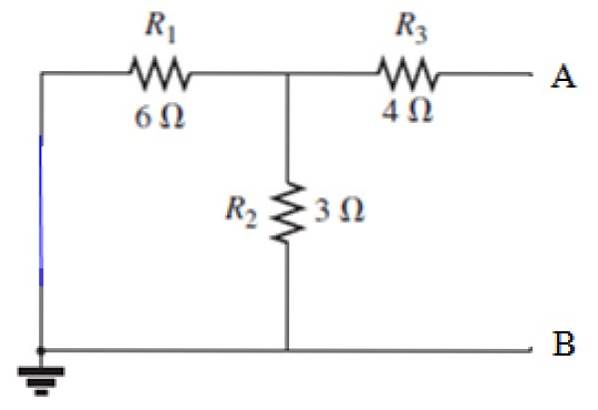
Beregning af RN
Udsigt fra terminal A og B, modstand R3 er i serie med parallellen dannet af modstandene R1 og Rto, lad os først beregne den tilsvarende modstand af denne parallel:
1 / R12 = (1/6) + (1/3) Ω-1 = 1/2 Ω-1 → Rækv = 2/1 Ω = 2Ω
Og så er denne parallel i serie med R3, således at den tilsvarende modstand er:
Rækv = 2 Ω + 4 Ω = 6 Ω
Dette er værdien af begge RN fra RTh, som forklaret før.
I beregning
Terminalerne A og B kortsluttes derefter og returnerer kilden til sin plads:
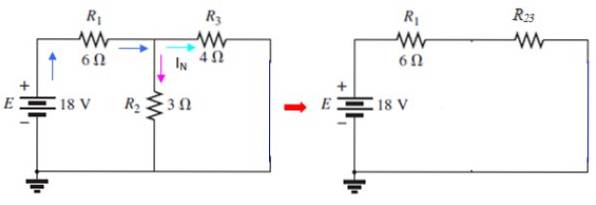
Strømmen gennem jeg3 er det nuværende jegN søges, som kan bestemmes ved hjælp af maskemetoden eller ved hjælp af serie og parallel. I dette kredsløb Rto og R3 er parallelle:
1 / R2. 3 = (1/3) + (1/4) Ω-1 = 7/12 Ω-1 → R2. 3 = 12/7 Ω
Modstanden R1 er i serie med denne parallel, så:
R123 = 6 + (12/7) Ω = 54/7 Ω
Strømmen, der forlader kilden (blå farve) beregnes ved hjælp af Ohms lov:
V = I. R → I = V / R = 18 V / (54/7 Ω) = 7/3 A
Denne strøm er opdelt i to dele: en der passerer gennem Rto og en anden, der krydser R3. Imidlertid er strømmen gennem parallel R2. 3 det er det samme, der går gennem R1, som det ses i det mellemliggende kredsløb i figuren. Spændingen der er:
V2. 3 = I.R2. 3 = (7/3) A. (12/7) Ω = 4 V
Begge modstande Rto og R3 er ved denne spænding, da de er parallelle, derfor:
jeg3 = V2. 3 / R3 = 4 V / 4 Ω = 1 A.
Vi har allerede søgt efter Norton-strømmen, da jeg som tidligere sagt3 = JegN, derefter:
jegN = 1 A.
Norton-ækvivalent
Alt er klar til at tegne Norton-ækvivalenten for dette kredsløb mellem punkterne A og B:
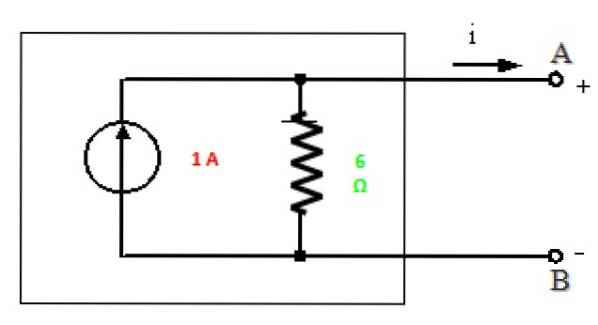
Løsning b
At finde Thévenin-ækvivalenten er meget simpelt, da RTh = RN= 6 Ω og som forklaret i de foregående afsnit:
VTh = JegN. RN = 1 A. 6 Ω = 6 V
Thévenin-ækvivalent kredsløb er:
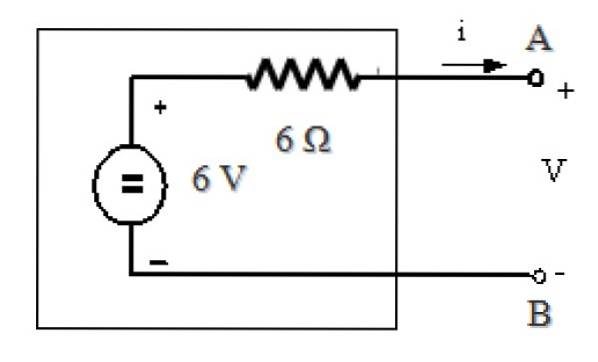
Referencer
- Alexander, C. 2006. Grundlæggende om elektriske kredsløb. 3. Udgave. Mc Graw Hill.
- Boylestad, R. 2011. Introduktion til kredsløbsanalyse. 2. plads Udgave. Pearson.
- Dorf, R. 2006. Introduktion til elektriske kredsløb. 7. Udgave. John Wiley & Sons.
- Edminister, J. 1996. Elektriske kredsløb. Schaum-serien. 3. Udgave. Mc Graw Hill.
- Wikipedia. Nortons sætning. Gendannet fra: es.wikipedia.org.


Endnu ingen kommentarer