Varignons sætning

Hvad er Varignons sætning?

Varignons sætning i Mekanik siger, at summen af ​​øjeblikke produceret af et system af samtidige kræfter i forhold til et bestemt punkt er lig med øjeblikket for den resulterende kraft i forhold til det samme punkt.

Af denne grund er denne sætning også kendt som begyndelsen på øjeblikke.

Selvom den første, der fortalte det, var hollænderen Simon Stevin (1548-1620), skaberen af ​​det hydrostatiske paradoks, var den franske matematiker Pierre Varignon (1654-1722) den, der senere gav det sin endelige form.

Et eksempel på, hvordan Varignons sætning fungerer inden for mekanik, er følgende: antag, at et simpelt system af to planplan og samtidige kræfter virker på et punkt F₁ Y F_to, (betegnet med fed skrift på grund af deres vektortegn). Disse kræfter giver anledning til en netto eller resulterende kraft, kaldet F_R.

Hver kraft udøver et drejningsmoment eller øjeblik omkring et punkt O, der beregnes af vektorproduktet mellem positionsvektoren r_OP og styrken F, hvor r_OP er dirigeret fra O til punktet for samtidighed P:

M_O1 = r_OP × F₁

M_O2 = r_OP × F_to

På grund af F_R = F₁ + F_to, derefter:

M_ELLER = r_OP × F₁ + r_OP × F_to = M_O1 + M_O2

Men hvordan r_OP er en fælles faktor, så anvendelse af distribuerende ejendom på krydsproduktet:

M_ELLER = r_OP × (F₁ + F_to) = r_OP × F_R                

Derfor er summen af ​​momentene eller drejningsmomenterne for hver kraft i forhold til punkt O svarende til momentet for den resulterende kraft i forhold til det samme punkt.

Erklæring og bevis

Lad være et system af N samtidige kræfter, dannet af F₁, F_to, F₃... F_N, hvis handlingslinjer krydser hinanden ved punkt P (se figur 1), øjeblikket for dette styrkesystem M_ELLER, med hensyn til et punkt O er givet ved:

M_ELLER = r_OP × F₁ + r_OP × F_to + r_OP × F₃ +... r_OP × F_N = r_OP × (F₁ + F_to + F₃ +... F_N)

Demonstration

For at bevise sætningen anvendes vektorens produktets distribuerende egenskab mellem vektorer.

Vær kræfterne F₁, F_to, F₃... F_N anvendt på punkt A₁, TIL_to, TIL₃… TIL_N og samtidig ved punkt P. Det resulterende øjeblik for dette system, med hensyn til et punkt O, kaldet M_ELLER, er summen af ​​øjeblikkene for hver kraft i forhold til det nævnte punkt:

M_ELLER = ∑ r_OAi × F_jeg

Hvor summen går fra i = 1 til i = N, da der er N-kræfter. Da vi har at gøre med samtidige kræfter, og da vektorproduktet mellem parallelle vektorer er nul, sker det, at:

r_PAi × F_jeg = 0

Med nulvektoren betegnet som 0.

Øjeblikket for en af ​​kræfterne i forhold til O, for eksempel kraftens F_jeg anvendt i A_jeg, det er skrevet sådan:

M_{jeg hørte} = r_OAi × F_jeg

Positionsvektoren r_OAi  kan udtrykkes som summen af ​​to positionsvektorer:

r_OAi = r_OP + r_PAi

På denne måde øjeblikket omkring O af styrken F_jeg det er:

M_{jeg hørte} = (r_OP + r_PAi) × F_jeg = (r_OP × F_jeg) + (r_PAi × F_jeg)

Men den sidste periode er nul, som forklaret ovenfor, fordi r_PAi er på linjen for F_jeg, Dermed:

M_{jeg hørte} = r_OP × F_jeg

Ved at vide, at systemets øjeblik med hensyn til punkt O er summen af ​​alle de enkelte øjeblikke for hver kraft i forhold til det nævnte punkt, så:

M_ELLER = ∑ M_{jeg hørte} = ∑ r_OP × F_jeg

Hvad r_OP er konstant kommer ud af summen:

M_ELLER = r_OP × (∑ F_jeg)

Men ∑ F_jeg er simpelthen nettokraften eller den resulterende kraft F_R, derfor konkluderes det straks, at:

M_ELLER = r_OP × F_R

Eksempel

Varignons sætning letter beregningen af ​​kraftmomentet F Med hensyn til punkt O i strukturen vist i figuren, hvis kraften nedbrydes i dens rektangulære komponenter, og øjeblikket for hver af dem beregnes:

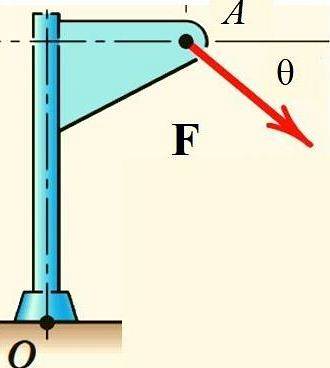
Anvendelser af Varignons sætning

Når den resulterende kraft i et system er kendt, kan Varignons sætning anvendes til at erstatte summen af ​​hvert af de øjeblikke, der produceres af de kræfter, der komponerer det med det resulterende øjeblik..

Hvis systemet består af kræfter på det samme plan, og det punkt, som momentet skal beregnes til, hører til det plan, er det resulterende øjeblik vinkelret.

For eksempel, hvis alle kræfterne er i xy-planet, dirigeres øjeblikket i z-aksen, og det forbliver kun at finde dens størrelse og dens sans, sådan er tilfældet med eksemplet beskrevet ovenfor.

I dette tilfælde giver Varignons sætning os mulighed for at beregne det resulterende øjeblik af systemet gennem summeringen. Det er meget nyttigt i tilfælde af et tredimensionelt styrkesystem, for hvilket retningen af ​​det resulterende øjeblik ikke er kendt på forhånd.

For at løse disse øvelser er det praktisk at nedbryde kræfter og placere vektorer i deres rektangulære komponenter, og ud fra summen af ​​øjeblikke bestemme komponenterne i nettomomentet.

Træning løst

Brug Varignons sætning til at beregne momentet for kraften F omkring punktet O vist i figuren, hvis størrelsen af ​​F er 725 N.

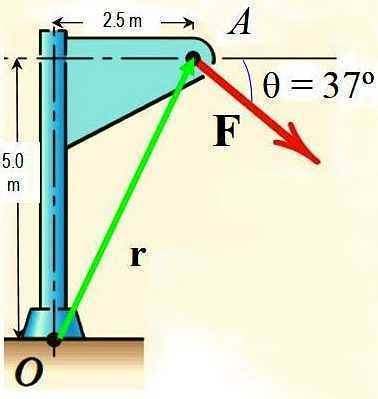
Opløsning

For at anvende Varignons sætning skal du nedbryde kraften F i to komponenter, hvis respektive øjeblikke omkring O beregnes og tilføjes for at opnå det resulterende øjeblik.

F_x = 725 N ∙ cos 37 º = 579,0 N

F_Y = - 725 N N ∙ sin 37 º = −436,3 N

Ligeledes placeringsvektoren r rettet fra O til A har komponenterne:

r_x = 2,5 m

r_Y = 5,0 m

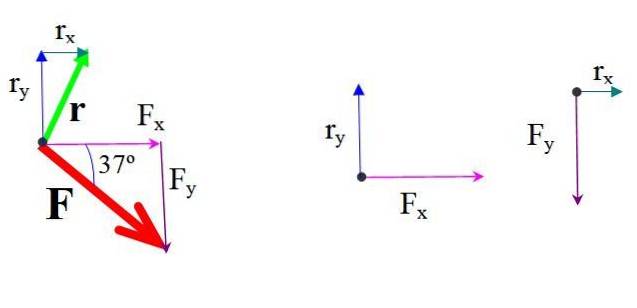
Momentet for hver komponent af kraften omkring O findes ved at multiplicere kraften og den vinkelrette afstand.

Begge kræfter har tendens til at rotere strukturen i samme retning, som i dette tilfælde er med uret, hvortil et positivt tegn vilkårligt er tildelt:

M_Okse = F_x∙ r_Y ∙ sin 90º = 579,0 N ∙ 5,0 m = 2895 N ∙ m

M_Oy = F_Y∙ r_x ∙ sin (−90º) = −436,3 N ∙ 2,5 m ∙ (−1) = 1090,8 N ∙ m

Det resulterende øjeblik omkring O er:

M_ELLER = M_Okse + M_Oy = 3985,8 N ∙ m vinkelret på planet og med uret.

Referencer

1. Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley. 
2. Beer, F. 2010. Statisk. McGraw Hill. 9. Udgave.
3. Hibbeler, R. 1992. Mekanik til ingeniører. 6. Udgave. CECSA.
4. HK Engineering. Varignons sætning. Gendannet fra: youtube.com.
5. Wikipedia. Varignons sætning (Mekanik). Gendannet fra: en.wikipedia.org.