
Binomial sætning bevis og eksempler
Det binomial sætning er en ligning, der fortæller os, hvordan vi udvikler et udtryk for formen (a + b)n for noget naturligt tal n. Et binomium er intet mere end summen af to elementer, som (a + b). Det giver os også mulighed for at vide for en periode, der er givet af enkbn-k hvad er koefficienten, der ledsager den.
Denne sætning tilskrives almindeligvis den engelske opfinder, fysiker og matematiker Sir Isaac Newton; Imidlertid er der fundet forskellige optegnelser, der indikerer, at dets eksistens allerede var kendt i Mellemøsten omkring år 1000.

Artikelindeks
- 1 Kombinationstal
- 2 demo
- 3 eksempler
- 3.1 Identitet 1
- 3.2 Identitet 2
- 4 Endnu en demonstration
- 4.1 Bevis ved induktion
- 5 nysgerrigheder
- 6 Referencer
Kombinationstal
Binomial sætningen fortæller os matematisk følgende:
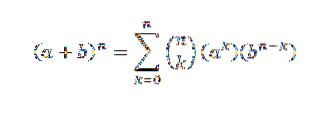
I dette udtryk er a og b reelle tal, og n er et naturligt tal.
Lad os se på nogle grundlæggende begreber, der er nødvendige, før vi giver dem.
Det kombinatoriske antal eller kombinationer af n i k udtrykkes som følger:
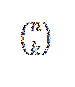
Denne form udtrykker værdien af, hvor mange delmængder med k-elementer, der kan vælges blandt et sæt n-elementer. Dets algebraiske udtryk er givet af:
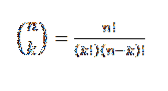
Lad os se et eksempel: Antag, at vi har en gruppe på syv bolde, hvoraf to er røde og resten er blå..
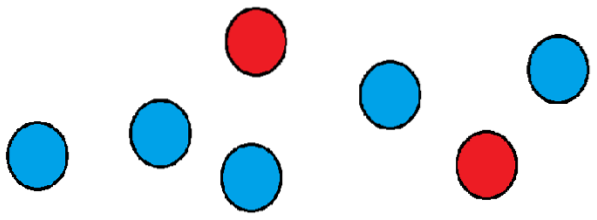
Vi vil vide, hvor mange måder vi kan arrangere dem i træk. En måde kunne være at placere de to røde i første og anden position, og resten af bolde i de positioner, der er tilbage..
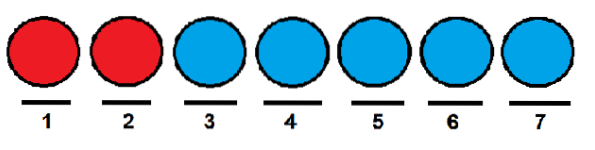
I lighed med det foregående tilfælde kunne vi give de røde kugler henholdsvis den første og sidste position og besætte de andre med blå kugler.
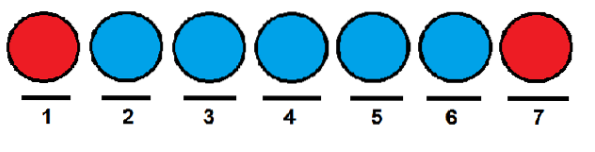
Nu er en effektiv måde at tælle på, hvor mange måder vi kan arrangere kuglerne i træk ved hjælp af kombinatoriske tal. Vi kan se hver position som et element i følgende sæt:
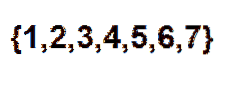
Så er det kun tilbage at vælge en delmængde af to elementer, hvor hvert af disse elementer repræsenterer den position, som de røde kugler vil indtage. Vi kan træffe dette valg i henhold til forholdet givet af:
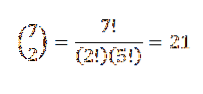
På denne måde har vi, at der er 21 måder at bestille disse bolde på.
Den generelle idé med dette eksempel vil være meget nyttig til at bevise binomial sætning. Lad os se på en bestemt sag: hvis n = 4, har vi (a + b)4, hvilket ikke er mere end:
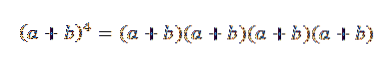
Når vi udvikler dette produkt, står vi tilbage med summen af de termer, der opnås ved at multiplicere et element af hver af de fire faktorer (a + b). Således har vi vilkår, der vil have formen:
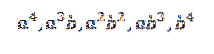
Hvis vi ønskede at få udtrykket fra formularen a4, multiplicer bare som følger:
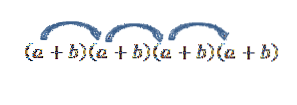
Bemærk, at der kun er én måde at opnå dette element på; men hvad sker der, hvis vi nu ser efter udtrykket for formularen atobto? Da “a” og “b” er reelle tal, og derfor er kommutativ lov gyldig, har vi den ene måde at opnå dette udtryk på er at formere sig med medlemmerne som angivet med pilene.
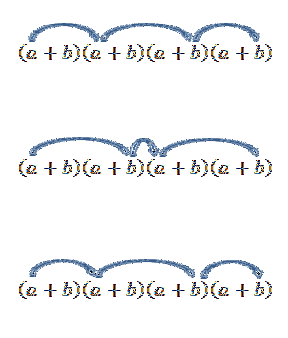
At udføre alle disse operationer er normalt kedeligt, men hvis vi ser udtrykket "a" som en kombination, hvor vi vil vide, hvor mange måder vi kan vælge to "a" fra et sæt af fire faktorer, kan vi bruge ideen fra forrige eksempel. Så vi har følgende:
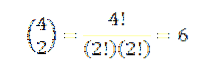
Således ved vi, at i den endelige udvidelse af udtrykket (a + b)4 vi vil have nøjagtigt 6atobto. Brug den samme idé til de andre elementer, skal du:
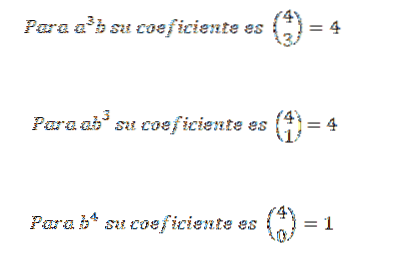
Derefter tilføjer vi de tidligere opnåede udtryk, og vi har det:
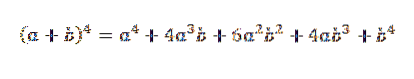
Det er et formelt bevis for det generelle tilfælde, hvor "n" er et hvilket som helst naturligt tal.
Demonstration
Bemærk, at de vilkår, der er tilbage, når du udvikler (a + b)n De er af form akbn-k, hvor k = 0,1,…, n. Ved hjælp af ideen i det foregående eksempel har vi måden at vælge "k" variabler "a" af "n" faktorer er:
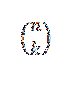
Ved at vælge på denne måde vælger vi automatisk n-k-variabler "b". Heraf følger, at:
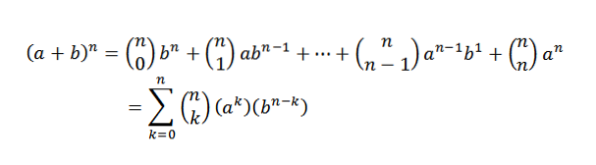
Eksempler
Overvejer (a + b)5, Hvad ville din udvikling være?
Ved binomial sætning har vi:
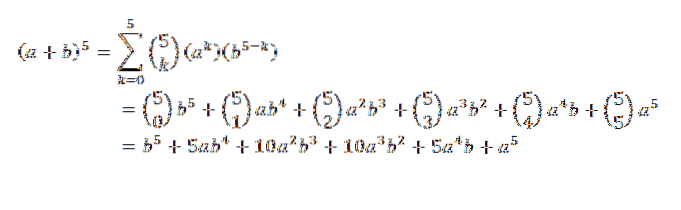
Binomial sætningen er meget nyttig, hvis vi har et udtryk, hvor vi vil vide, hvad koefficienten for et bestemt udtryk er uden at skulle udføre den fulde udvidelse. Som et eksempel kan vi tage følgende ukendte: hvad er koefficienten for x7Y9 i udvidelsen af (x + y)16?
Ved binomial sætning har vi, at koefficienten er:
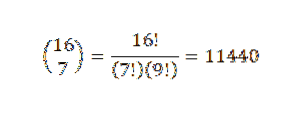
Et andet eksempel ville være: hvad er koefficienten for x5Y8 i udviklingen af (3x-7y)13?
Først omskriver vi udtrykket på en bekvem måde; dette er:
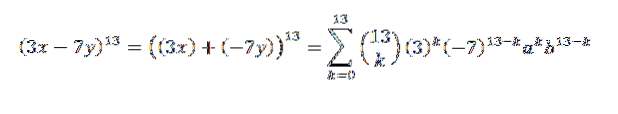
Derefter ved hjælp af binomial sætning har vi, at den ønskede koefficient er, når vi har k = 5
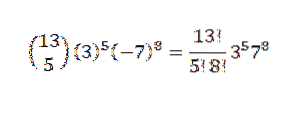
Et andet eksempel på anvendelsen af denne sætning er beviset for nogle almindelige identiteter, såsom dem, som vi vil nævne nedenfor.
Identitet 1
Hvis "n" er et naturligt tal, har vi:
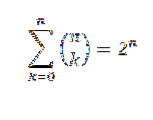
Til beviset bruger vi binomial sætning, hvor både "a" og "b" tager værdien af 1. Så har vi:
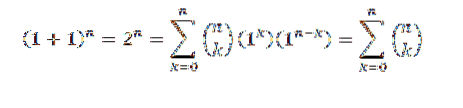
På denne måde har vi bevist den første identitet.
Identitet 2
Hvis "n" er et naturligt tal, så
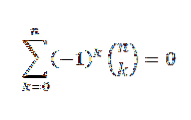
Ved binomial sætning har vi:
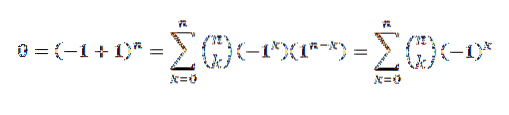
Endnu en demonstration
Vi kan fremstille et andet bevis for binomial sætning ved hjælp af den induktive metode og Pascals identitet, som fortæller os, at hvis "n" og "k" er positive heltal, der tilfredsstiller n ≥ k, så:
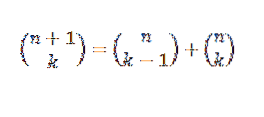
Induktionssikker
Lad os først se, at den induktive base holder. Hvis n = 1, har vi:
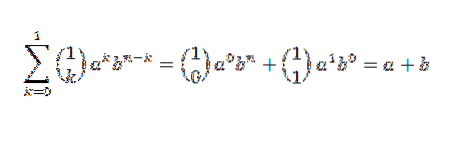
Faktisk ser vi, at det er opfyldt. Lad nu n = j sådan, at:
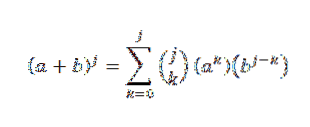
Vi vil se, at for n = j + 1 er det sandt, at:
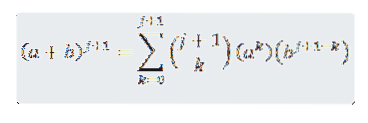
Så vi skal:
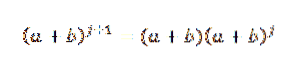
Ved hypotese ved vi, at:
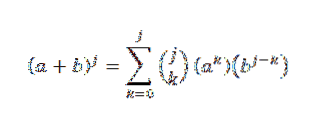
Brug derefter den distribuerende egenskab:
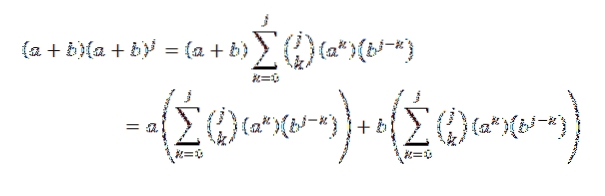
Efterfølgende har vi udviklet hver af opsummeringerne:
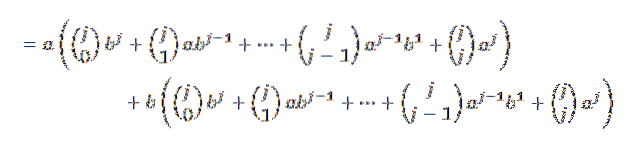
Nu, hvis vi grupperer på en bekvem måde, har vi det:
Ved hjælp af Pascals identitet har vi:
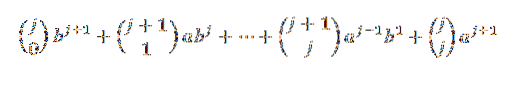
Endelig bemærk at:
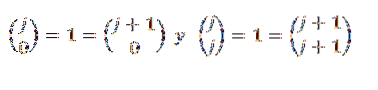
Derfor ser vi, at binomial sætningen gælder for alle "n", der hører til de naturlige tal, og med dette ender beviset.
Nysgerrigheder
Det kombinatoriske tal (nk) kaldes også binomialkoefficienten, fordi det netop er koefficienten, der vises i udviklingen af binomialet (a + b)n.
Isaac Newton gav en generalisering af denne sætning for det tilfælde, hvor eksponenten er et reelt tal; denne sætning er kendt som Newtons binomiale sætning.
Allerede i oldtiden var dette resultat kendt for det særlige tilfælde, hvor n = 2. Denne sag er nævnt i Elementer af Euclid.
Referencer
- Johnsonbaugh Richard. Diskret matematik. PHH
- Kenneth.H. Rosen. Diskret matematik og dens anvendelser. S.A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Seymour Lipschutz Ph.D & Marc Lipson. Diskret matematik. McGRAW-HILL.
- Ralph P. Grimaldi. Diskret matematik og kombinatorik. Addison-Wesley Iberoamericana
- Verde Star Luis ... Diskret og kombinatorisk matematik.Anthropos



Endnu ingen kommentarer