Det job I fysik er det overførsel af energi, der udføres af en kraft, når objektet, som det virker på, bevæger sig. Matematisk tager det form af det skalære produkt mellem kraftvektorerne F og forskydning s.
Og da det skalære produkt mellem to vinkelrette vektorer er nul, sker det, at de kræfter, der danner 90 ° med forskydningen, ikke fungerer ifølge definitionen, da:
W = F ● s = F⋅ s⋅ cos θ
Hvor W betegner arbejde, fra det engelske ord arbejde.
Fordelen ved at definere arbejdet er, at det er en skalar, det vil sige, det har ingen retning eller sans, kun modul og den respektive enhed. Dette gør det lettere at udføre beregninger, der involverer energiforandringer forårsaget af kræfternes virkning..
Tyngdekraft og kinetisk friktion er eksempler på kræfter, der ofte virker på bevægelige genstande. En anden almindelig kraft er den normale, der udøves af en overflade, men i modsætning til dem fungerer den aldrig på genstande, da den er vinkelret på forskydningen..
Når et legeme falder frit, fungerer tyngdekraften positivt på mobilen, hvilket får det til at øge sin hastighed, når det falder. På den anden side har kinetisk friktion en helt modsat virkning, da den altid modsætter sig bevægelse, den udfører negativt arbejde, der ikke favoriserer det..
Artikelindeks
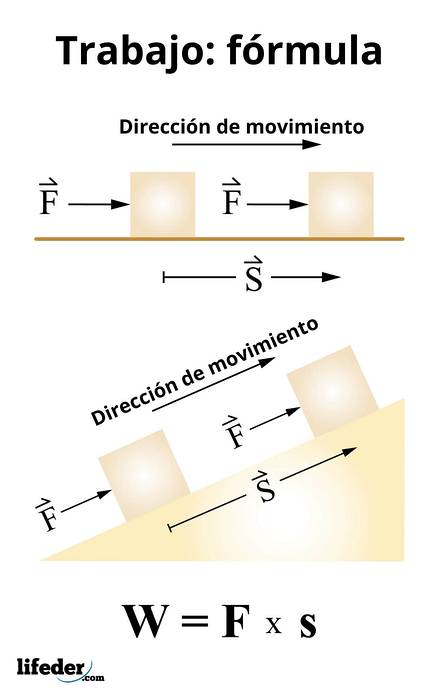
Arbejdet beregnes af:
W = F ● s
Dette udtryk er gyldigt for konstante kræfter og ifølge definitionen af et skalarprodukt svarer det til:
W = F. s. cos θ
Hvor θ er vinklen mellem kraften og forskydningen. Det følger derfor, at kun de kræfter, der har en komponent i forskydningsretningen, kan arbejde på et legeme.
Og det bliver også klart, at hvis der ikke er nogen bevægelse, er der heller ikke noget arbejde.
Med hensyn til tegnet kan arbejdet være positivt, negativt eller nul. Hvis kraften har en komponent, der er parallel med bevægelsen, afhænger arbejdets tegn af værdien af cos θ.
Der er nogle særlige tilfælde, der er værd at overveje:
W = F⋅s cos 0º = F⋅s
W = F⋅s cos 180º = -F⋅s
W = F⋅s cos 90º = 0
Nogle gange er den anvendte kraft ikke konstant; i så fald skal du ty til beregning for at finde det udførte arbejde. For det første bestemmes en arbejdsforskel dW, udført på en uendelig minimal forskydning ds:
dW = F⋅ds
For at finde værdien af det samlede arbejde udført af denne kraft, når objektet går fra punkt A til punkt B, er det nødvendigt at integrere begge sider på denne måde:
Enheden til arbejde i det internationale system er joule, forkortet J. Enheden stammer fra den engelske fysiker James Prescott Joule, en pioner inden for studiet af termodynamik..
Fra arbejdsligningen defineres joule som 1 newton pr. Meter:
1 J = 1 Nm
Arbejde svarer som en enhed pund-kraft x fod, undertiden ringe pund-kraft fod. Det er også en enhed til energi, men det skal huskes, at arbejde udført på en krop ændrer sin energitilstand, og at arbejde og energi derfor er ækvivalente. Ikke underligt, at de har de samme drev.
Ækvivalensen mellem pund-kraftfoden og joule er som følger:
1 fod-pund-kraft = 1.35582 J
En velkendt enhed til arbejde og energi, især inden for køling og klimaanlæg, er BTU eller Britisk termisk enhed.
1 BTU er lig med 1055 J og 778.169 fodpund-kraft.
Der er andre enheder til arbejde, der bruges i bestemte områder inden for fysik og teknik. Blandt dem har vi:
Betegnet som erg, er arbejdsenheden i cegesimal-systemet og er lig med 1 dyna⋅cm eller 1 x 10-7 J.
Forkortet eV, det bruges almindeligvis i partikelfysik og defineres som den energi, som en elektron erhverver, når den bevæger sig gennem en potentialforskel på 1 V.
Det vises ofte på regninger. Det er det arbejde, der udføres i løbet af 1 time af en kilde, hvis effekt er 1 kW, svarende til 3,6 x 106 J.
Det er normalt relateret til madens energi, selvom der i denne sammenhæng faktisk henvises til a kilokalorie, 1000 kalorier. Der er faktisk flere enheder, der modtager dette navn, så konteksten skal specificeres meget godt.
Ækvivalensen mellem joule og 1 termokemisk kalorie det er:
1 kalorieindhold = 4,1840 J
Når kroppe ned, enten lodret eller ned ad en rampe, fungerer vægten positivt og favoriserer bevægelse. I stedet, når et objekt stiger op, fungerer tyngdekraften negativt.
Et ensartet elektrisk felt fungerer på en punktladning, der bevæger sig inde i det. Afhængigt af feltet og ladningens tegn kan dette arbejde være negativt eller positivt.
Kinetisk friktion mellem overflader fungerer altid negativt på den bevægelige genstand.
At skubbe er en kraft, der trækker et objekt væk fra noget. At trække er en kraft, der får et objekt til at nærme sig selv.
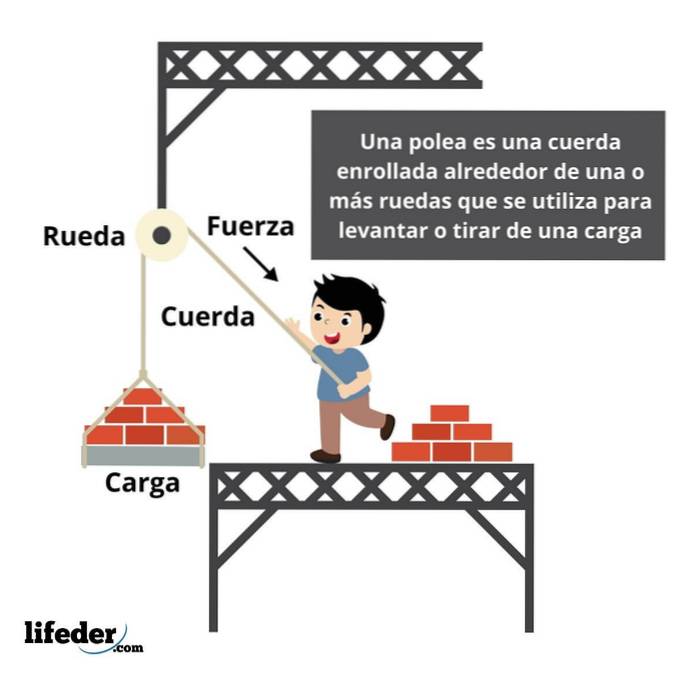
En remskive er et system, der bruges til at transmittere en kraft fra en af dens ender. I en simpel remskive, for at løfte lasten, skal der påføres en kraft svarende til modstanden, der udøves af objektet.
Det normale fungerer, som nævnt ovenfor, nul, når en genstand, der hviler på en overflade, bevæger sig på den, selvom overfladen ikke er flad eller hvis den er skråt..
En anden kraft, der ikke fungerer nul, er den magnetiske kraft, der udøver et ensartet felt på den ladede partikel, der er vinkelret på den. Partiklens bevægelse viser sig at være en ensartet cirkulær bevægelse med kraften i radial retning. Da forskydningen er vinkelret på kraften, fungerer den ikke på belastningen..
Et reb arbejder heller ikke på et ophængt pendul, da spændingen i det altid er vinkelret på forskydningen af massen..
Tyngdekraften fungerer heller ikke på en satellit i cirkulær bane af samme grund som de tidligere tilfælde: den er vinkelret på forskydningen..
I et massefjedersystem, kraften F at foråret udøver på massen har størrelse F = kx, hvor k er foråret konstant og x dens kompression eller forlængelse. Det er en variabel kraft, og derfor afhænger arbejdet af, hvor meget fjederen strækker sig eller krymper.
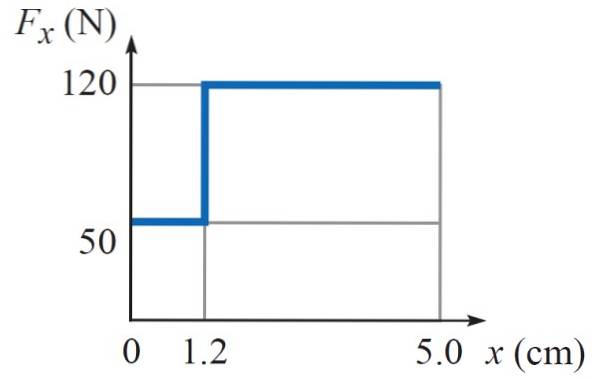
Den følgende graf viser arbejdet udført med en variabel kraft Fx hvilket afhænger af positionen x. Dette er den kraft, der udøves af en hammer på et søm. Den første del er den kraft, der bruges til at sømme på den blødere del af væggen, og den anden til at færdiggøre neglen.
Hvor meget arbejde skal hammeren gøre for, at neglen synker i alt 5 cm ned i væggen?
Kraften, som hammeren udøver, er variabel, da der kræves mindre intensitet (50 N) for at drive neglen 1,2 cm ind i den bløde del af væggen, mens det i den hårdere del tager 120 N at få neglen til at synke ned til 5 cm dyb, som vist i diagrammet.
I dette tilfælde er arbejdet integreret:
Hvor A = 0 cm og B = 5 cm. Da integralet er området under grafen Fx vs x, er det nok at finde dette område, der svarer til to rektangler, den første med højde 50 N og bredde 1,2 cm, og den anden med højde 120 N og bredde (5 cm - 1,2 cm) = 3,8 cm.
Begge beregnes og tilføjes for at give det samlede arbejde:
B = 50 N x 1,2 cm + 120 N x 3,8 cm = 516 N. cm = 516 N x 0,01 m = 5,16 J.
Endnu ingen kommentarer