Det mekanisk arbejde Det defineres som ændringen i et systems energitilstand forårsaget af virkningen af eksterne kræfter såsom tyngdekraft eller friktion. Enhederne til mekanisk arbejde i det internationale system (SI) er newton x meter eller joule, forkortet med J.
Matematisk defineres det som det skalære produkt af kraftvektoren og forskydningsvektoren. Ja F er den konstante kraft og l er forskydningen, begge vektorer, værket W udtrykkes som: W = F ● l
Når kraften ikke er konstant, skal vi analysere det arbejde, der er udført, når forskydningerne er meget små eller differentierede. I dette tilfælde, hvis punkt A betragtes som startpunktet og B som ankomstpunktet, opnås det samlede arbejde ved at tilføje alle bidragene til det. Dette svarer til beregning af følgende integral:
Variation i energi i systemet = Arbejde udført af eksterne kræfter
ΔE = Wekst
Når energi tilføjes systemet, W> 0 og når energi trækkes W<0. Ahora bien, si ΔE = 0, puede significar que:
-Systemet er isoleret, og der er ingen eksterne kræfter, der virker på det.
-Der er eksterne kræfter, men de arbejder ikke på systemet.
Da ændringen i energi er lig med det arbejde, der udføres af eksterne kræfter, er SI-enheden af energi også joule. Dette inkluderer enhver form for energi: kinetisk, potentiale, termisk, kemisk og mere..
Artikelindeks
Vi har allerede set, at arbejde er defineret som et punktprodukt. Lad os tage definitionen af arbejde udført med en konstant kraft og anvende begrebet prikprodukt mellem to vektorer:
W = F ● l = F.l.cos θ
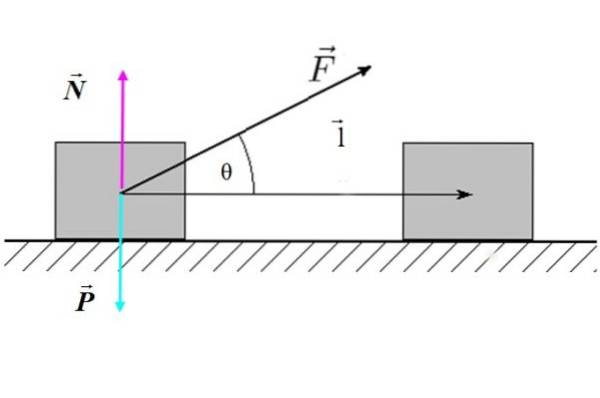
Hvor F er kraftens størrelse, l er størrelsen af forskydningen og θ er vinklen mellem kraften og forskydningen. I figur 2 er der et eksempel på en skrå ekstern kraft, der virker på en blok (systemet), der producerer en vandret forskydning.
Omskrivning af arbejdet som følger:
W = (F. cos θ). l
Vi kan sige, at kun den del af kraften, der er parallel med forskydningen: F. cos θ eer i stand til at udføre arbejde. Hvis θ = 90 º, så er cos θ = 0, og arbejdet ville være nul.
Derfor konkluderes det, at kræfterne vinkelret på forskydningen ikke udfører mekanisk arbejde.
I tilfælde af figur 2 hverken den normale kraft N ej heller vægten P arbejde, da begge er vinkelrette på forskydningen l.
Som forklaret ovenfor, W Det kan være positivt eller negativt. Når cos θ> 0, arbejdet udført af kraften er positivt, da det har samme bevægelsesretning.
Ja cos θ = 1, kraft og forskydning er parallelle og arbejde er maksimalt.
I tilfælde cos θ < 1, la fuerza no está a favor del movimiento y el trabajo es negativo.
Hvornår cos θ = -1, kraft er helt modsat forskydning, såsom kinetisk friktion, hvis virkning er at bremse objektet, som det virker på. Så arbejdet er minimalt.
Dette stemmer overens med det, der blev sagt i starten: Hvis arbejdet er positivt, tilføjes energi til systemet, og hvis det er negativt, trækker det.
Netto arbejde Wnet Det defineres som summen af arbejdet udført af alle de kræfter, der virker på systemet:
Wnet = ∑Wjeg
Derefter kan vi konkludere, at for at garantere eksistensen af nettomekanisk arbejde er det nødvendigt, at:
-Eksterne kræfter virker på objektet.
-Disse kræfter er ikke alle vinkelrette på forskydningen (cos θ ≠ 0).
-De job, der udføres af hver styrke, annullerer ikke hinanden.
-Der er en forskydning.
-Når det er nødvendigt at sætte et objekt i bevægelse fra hvile, er det nødvendigt at udføre mekanisk arbejde. For eksempel at skubbe et køleskab eller en tung kuffert på en vandret overflade.
-Et andet eksempel på en situation, hvor du skal udføre mekanisk arbejde, er at ændre hastigheden på en kugle i bevægelse..
-Der kræves arbejde for at hæve en genstand til en bestemt højde over gulvet.
Nu er der lige så almindelige situationer, hvor ikke arbejdet bliver gjort, selvom udseendet indikerer andet. Vi har sagt, at for at løfte en genstand til en bestemt højde skal du udføre arbejde, så vi bærer genstanden, løfter den over vores hoved og holder den der. Gør vi arbejde?
Tilsyneladende ja, for hvis genstanden er tung, vil armene trætte på kort tid, uanset hvor hårdt det er, udføres der ikke noget arbejde set fra fysikens synspunkt. Hvorfor ikke? Nå, fordi objektet ikke bevæger sig.
Et andet tilfælde, hvor det på trods af en ekstern kraft ikke udfører mekanisk arbejde, når partiklen har en ensartet cirkulær bevægelse.
For eksempel et barn, der spinder en sten bundet til en streng. Strengspændingen er den centripetale kraft, der gør det muligt for stenen at rotere. Men på alle tidspunkter er denne kraft vinkelret på forskydningen. Så udfører han ikke mekanisk arbejde, selvom det favoriserer bevægelse.
Systemets kinetiske energi er den, det besidder i kraft af dets bevægelse. Ja m er massen og v er bevægelseshastigheden, betegnes den kinetiske energi med K og er givet af:
K = ½ mvto
En definitions kinetiske energi kan pr. Definition ikke være negativ, da både massen og kvadratet af hastigheden altid er positive størrelser. Den kinetiske energi kan være 0, når objektet er i ro.
For at ændre et systems kinetiske energi er det nødvendigt at variere dets hastighed - vi vil overveje, at massen forbliver konstant, selvom dette ikke altid er tilfældet. Dette kræver udførelse af nettoarbejde på systemet, derfor:
Wnet = ΔK
Dette er arbejdet - kinetisk energi sætning. Det hedder, at:
Nettoarbejde er lig med ændringen i systemets kinetiske energi
Bemærk, at selvom K altid er positiv, kan ΔK være positiv eller negativ, da:
ΔK = Kendelig - K initial
Ja Kendelig >K initial systemet har fået energi og ΔK> 0. Tværtimod, hvis Kendelig < K initial, systemet har givet op strøm.
Når en fjeder strækkes (eller komprimeres), skal der udføres arbejde. Dette arbejde opbevares om foråret, så dette igen kan arbejde på f.eks. En blok, der er fastgjort til en af dens ender..
Hookes lov siger, at den kraft, der udøves af en fjeder, er en genoprettende kraft - den er i strid med forskydning - og også proportional med forskydningen. Proportionalitetskonstanten afhænger af, hvordan fjederen er: blød og let deformerbar eller stiv.
Denne kraft er givet af:
Fr = -kx
I udtrykket, Fr er kraften, k er foråret konstant og x er forskydningen. Det negative tegn indikerer, at den kraft, der udøves af fjederen, modsætter sig forskydningen.
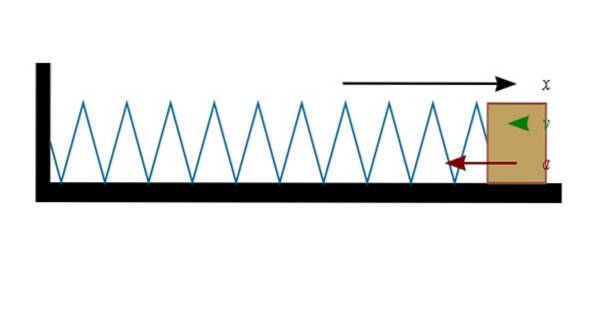
Hvis fjederen er komprimeret (til venstre i figuren), vil blokken i sin ende bevæge sig til højre. Og når fjederen strækkes (til højre), vil blokken bevæge sig til venstre.
For at komprimere eller strække fjederen skal en ekstern agent udføre arbejdet, og da det er en variabel kraft, skal vi beregne det nævnte arbejde ved at bruge definitionen i starten:
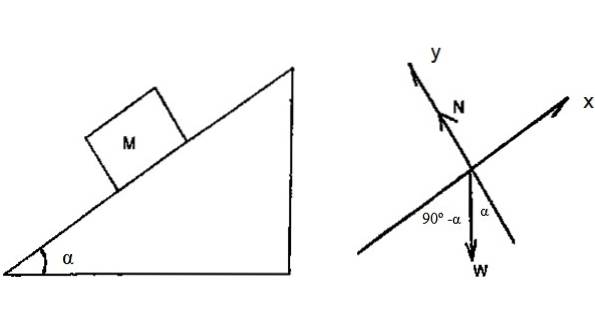
Det er meget vigtigt at bemærke, at dette er det arbejde, der udføres af den eksterne agent (for eksempel en persons hånd) for at komprimere eller strække fjederen. Derfor vises det negative tegn ikke. Og da positionerne er kvadratiske, betyder det ikke noget, om de er kompressioner eller strækninger..
Arbejdet, som foråret igen vil udføre på blokken, er:
Wforår = -Wekst
Blokken i figur 4 har masse M = 2 kg og glider nedad i det skrå plan uden friktion, med α = 36,9º. Antages det, at det er tilladt at glide fra hvile fra toppen af planet, hvis højde er h = 3 m, find den hastighed, hvormed blokken når bunden af planet ved hjælp af den arbejdskinetiske energisætning.
Diagrammet for frit legeme viser, at den eneste kraft, der er i stand til at udføre arbejde på blokken, er vægten. Mere præcis: vægtkomponenten langs x-aksen.
Den tilbagelagte afstand med blokken på flyet beregnes ved hjælp af trigonometri:
d = 3 / (cos 36,9º) m = 3,75 m
Wvægt = (Mg). d. cos (90-α) = 2 x 9,8 x 3,75 x cos 53,1 º J = 44,1 J
Ved arbejdskinetisk energisætning:
Wnet = ΔK
Wnet = Wvægt
ΔK = ½ MvFto- ½ Mvellerto
Da det er frigivet fra hvile, veller = 0, Dermed:
Wnet = ½ MvFto
En vandret fjeder, hvis konstant er k = 750 N / m, er fastgjort i den ene ende til en væg. En person komprimerer den anden ende en afstand på 5 cm. Beregn: a) Den kraft, personen udøver, b) Det arbejde, han udførte for at komprimere fjederen.
a) Størrelsen af den kraft, der påføres af personen, er:
F = kx = 750 N / m. 5x10 -to m = 37,5 N.
b) Hvis enden af fjederen oprindeligt er på x1 = 0, for at tage det derfra til den endelige position xto = 5 cm, det er nødvendigt at udføre følgende arbejde i henhold til resultatet opnået i det foregående afsnit:
Wekst = ½ k (xtoto - x1to) = 0,5 x 750 x (0,05to -0toJ = 0,9375 J.
Endnu ingen kommentarer