
Trapezoid scalene egenskaber, formler og ligninger, eksempler
EN trapes scalene er en polygon med fire sider, hvoraf to er parallelle med hinanden og med sine fire indvendige vinkler af forskellige mål.
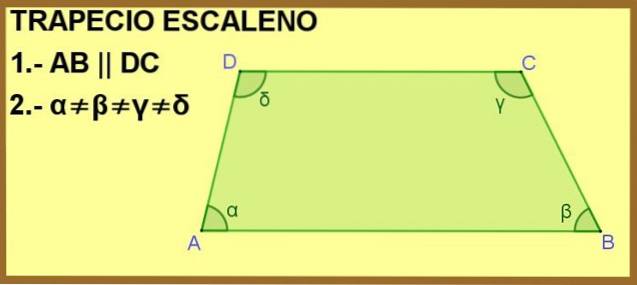
Den firesidede ABCD er vist nedenfor, hvor siderne AB og DC er parallelle med hinanden. Dette er nok til at gøre det til et trapezformet, men derudover er de indvendige vinkler α, β, γ og δ forskellige, derfor er trapezoidet scalene.
Artikelindeks
- 1 Elementer af scalene trapezium
- 1.1 Andre trapezoider
- 2 egenskaber
- 3 Formler og ligninger
- 3.1 Højde
- 3.2 Median
- 3.3 Diagonaler
- 3.4 Omkreds
- 3.5 Område
- 3.6 Andre forhold for scalene trapezium
- 4 Konstruktion af den scalene trapezform med lineal og kompas
- 5 Eksempel
- 5.1 - Løsning a
- 5.2 - Løsning b
- 6 Øvelse løst
- 6.1 Løsning
- 7 Referencer
Elementer af scalene trapezium
Her er de mest karakteristiske elementer:
-Baser og sider: trapezens parallelle sider er dens baser, og de to ikke-parallelle sider er laterale.
I en scalene trapezform er baserne af forskellige længder og de laterale også. Imidlertid kan en scalene trapezoid have en lateral lige længde til en base..
-Median: er det segment, der slutter sig til lateralernes midtpunkter.
-Diagonaler: diagonalen af en trapez er det segment, der forbinder to modstående hjørner. En trapez har, ligesom hver firkant, to diagonaler. I den scalene trapezform har de forskellige længder.
Andre trapezoider
Ud over den scalene trapezoid er der andre bestemte trapezoider: den højre trapezoid og den ligebenede trapezoid..
En trapez er et rektangel, når en af dens vinkler er rigtig, mens en ligebenet trapez har siderne af samme længde.
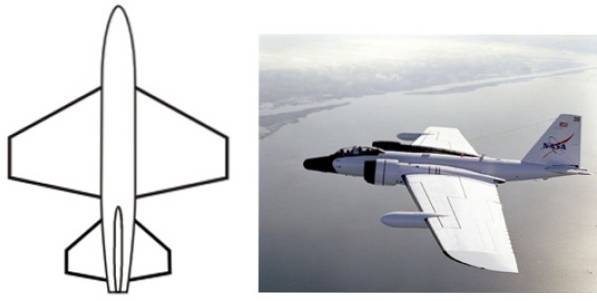
Den trapezformede form har adskillige anvendelser på design- og industriniveau, såsom i konfigurationen af flyvinger, formen på hverdagsgenstande såsom borde, stolrygger, emballage, punge, tekstilprint og mere..
Ejendomme
Nedenfor er egenskaberne af scalene trapezoid, hvoraf mange strækker sig til de andre typer trapezoid. I det følgende, når vi taler om "trapez", vil ejendommen være anvendelig til enhver type, inklusive scalene..
1. Medianen af trapezformet, det vil sige det segment, der forbinder midtpunkterne på dets ikke-parallelle sider, er parallel med nogen af baserne.
2. - Trapezens median har en længde, der er semisummen af dens baser og skærer sine diagonaler ved midtpunktet.
3.- Trapezens diagonaler krydser hinanden ved et punkt, der deler dem i to sektioner, der er proportionale med kvoterne i baserne.
4.- Summen af kvadraterne af diagonalerne på en trapez er lig med summen af kvadraterne på siderne plus det dobbelte produkt af baserne..
5.- Det segment, der slutter sig til diagonalernes midtpunkter, har en længde svarende til halvforskellen mellem baserne.
6. - Vinklerne ved siden af de laterale er supplerende.
7.- I en scalene trapezform er længden af dens diagonaler forskellig.
8.- En trapez har kun en indskrevet omkreds, hvis summen af dens baser er lig med summen af dens sider.
9.- Hvis en trapez har en indskrevet omkreds, så er vinklen med toppunktet i midten af omkredsen og sider, der passerer gennem enderne af trapezens side lige.
10.- En scalene trapez har ikke en begrænset omkreds, den eneste type trapez, der har en er ligebenede.
Formler og ligninger
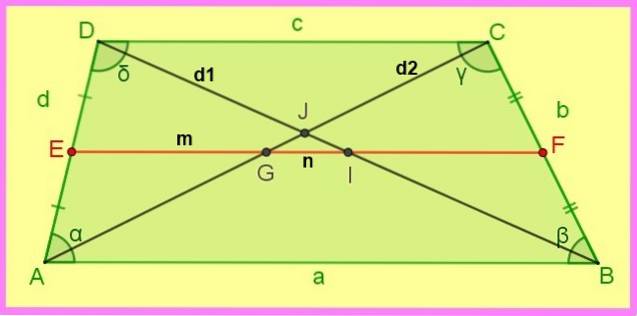
Følgende forhold mellem den scalene trapezoid henvises til den følgende figur.
1.- Hvis AE = ED og BF = FC → EF || AB og EF || DC.
2.- EF = (AB + DC) / 2, det vil sige: m = (a + c) / 2.
3.- DI = IB = d1 / 2 og AG = GC = dto /to.
4.- DJ / JB = (c / a) på samme måde CJ / JA = (c / a).
5.- DBto + ACto = ADto + F.Kr.to + 2 AB ∙ DC
Tilsvarende:
d1to + dtoto = dto + bto + 2 a ∙ c
6.- GI = (AB - DC) / 2
Nemlig:
n = (a - c) / 2
7.- α + δ = 180⁰ og β + γ = 180⁰
8.- Hvis α ≠ β ≠ γ ≠ δ så er d1 ≠ d2.
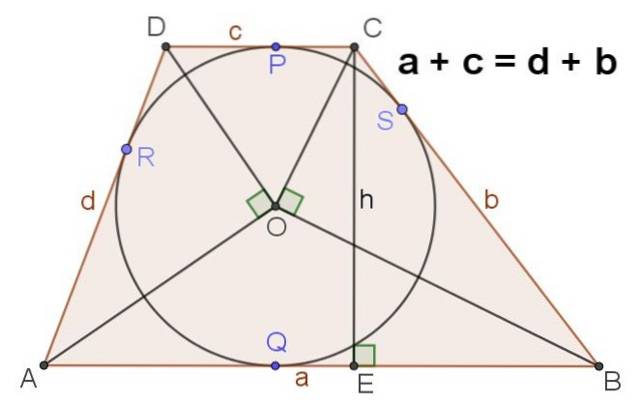
9.- Figur 4 viser en scalene trapezoid, der har en indskrevet omkreds, i dette tilfælde er det rigtigt, at:
a + c = d + b
10.- I en scalene trapezformet ABCD med en indskrevet omkreds af centrum O gælder følgende også:
∡AOD = ∡BOC = 90⁰
Højde
Højden af en trapez er defineret som det segment, der går fra et punkt af basen vinkelret på den modsatte base (eller til dens forlængelse).
Alle trapezens højder har samme måling h, så det meste af tiden refererer ordet højde til dets måling. I syntese er højden afstanden eller adskillelsen mellem baserne.
Højden h kan bestemmes ved at kende længden på den ene side og en af vinklerne ved siden af siden:
h = d Sen (α) = d Sen (γ) = b Sen (β) = b Sen (δ)
Median
Mål m for trapezens median er halvsummen af baserne:
m = (a + b) / 2
Diagonaler
d1 = √ [ato + dto - 2 ∙ a ∙ d ∙ Cos (α)]
dto= √ [ato + bto - 2 ∙ a ∙ b ∙ Cos (β)]
Det kan også beregnes, hvis kun længden af trapesformens sider er kendt:
d1 = √ [bto + a ∙ c - a (bto - dto) / (a - c)]
dto = √ [dto + a ∙ c - a (dto - bto) / (a - c)]
Omkreds
Omkredsen er den samlede længde af konturen, det vil sige summen af alle dens sider:
P = a + b + c + d
Areal
Arealet af en trapez er halvsummen af dens baser ganget med dens højde:
A = h ∙ (a + b) / 2
Det kan også beregnes, hvis medianen m og højde h er kendt:
A = m ∙ h
Hvis kun længden af siderne af trapezoidet er kendt, kan området bestemmes ved hjælp af Herons formel for trapezformet:
A = [(a + c) / | a-c |] ∙ √ [(s-a) (s-c) (s-a-d) (s-a-b)]
Hvor s er semiperimeteret: s = (a + b + c + d) / 2.
Andre forhold for scalene trapez
Skæringspunktet mellem medianen og diagonalerne og parallellen, der passerer gennem skæringen mellem diagonalerne, giver anledning til andre forhold.
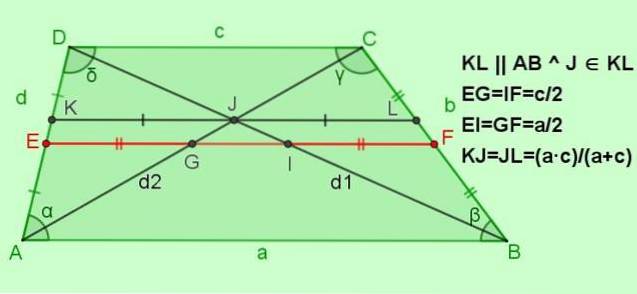
-Forhold til median EF
EF = (a + c) / 2; EG = IF = c / 2; EI = GF = a / 2
-Forholdet til segmentet parallelt med baserne KL og passerer gennem punktet J krydset mellem diagonalerne
Hvis KL || AB || DC med J ∈ KL, derefter KJ = JL = (a ∙ c) / (a + c)
Konstruktion af den scalene trapezform med lineal og kompas
I betragtning af længderne til Y c, hvor a> c og med sider af længderne b og d, være b> d, fortsæt ved at følge disse trin (se figur 6):
1.- Med reglen tegnes segmentet af det store AB.
2.- Fra A se og på AB markeres punktet P således, at AP = c.
3.- Med kompasset med centrum ved P og radius d tegnes en bue.
4.- Centrer ved B med radius b tegner en bue, der opfanger buen, der er tegnet i det foregående trin. Vi kalder Q skæringspunktet.
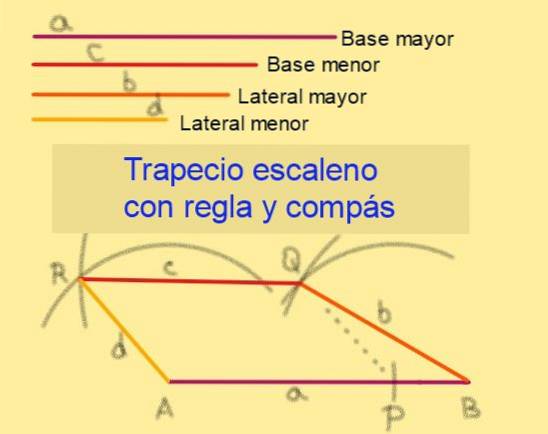
5.- Med midten ved A tegner du en bue med radius d.
6. - Med midten ved Q tegner du en bue med radius c, der opfanger buen trukket i det foregående trin. Afskæringspunktet kaldes R.
7. - Segmenter BQ, QR og RA spores med linealen.
8.- Det firsidede ABQR er en scalene trapezoid, da APQR er et parallelogram, der garanterer, at AB || Qr.
Eksempel
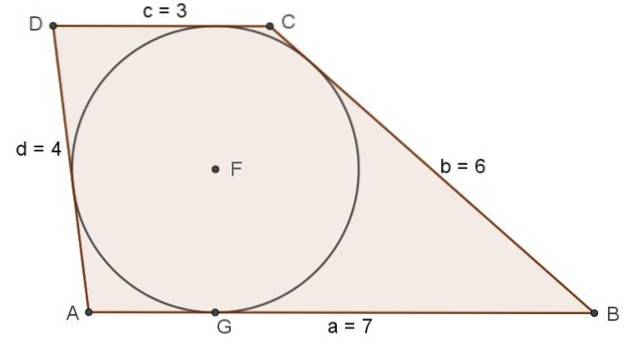
Følgende længder er angivet i cm: 7, 3, 4 og 6.
a) Find ud af, om det med dem er muligt at konstruere en scalene trapezform, der kan omringe en cirkel.
b) Find omkredsen, arealet, længden af diagonalerne og trapezens højde samt radius af den indskrevne cirkel.
- Løsning til
Ved anvendelse af segmenterne med længde 7 og 3 som baser og dem med længde 4 og 6 som laterale kan en scalene trapezoid konstrueres ved hjælp af proceduren beskrevet i det foregående afsnit.
Det er fortsat at kontrollere, om den har en indskrevet omkreds, men husk ejendommen (9):
En trapez har kun en indskrevet omkreds, hvis summen af dens baser er lig med summen af dens sider.
Vi ser det effektivt:
7 + 3 = 4 + 6 = 10
Derefter er betingelsen for eksistens af indskrevet omkreds opfyldt.
- Løsning b
Omkreds
Området P opnås ved at tilføje siderne. Da baserne tilføjes op til 10 og lateralerne også, er omkredsen:
P = 20 cm
Areal
For at bestemme området, der kun er kendt af dets sider, anvendes forholdet:
A = [(a + c) / | a-c |] ∙ √ [(s-a) (s-c) (s-a-d) (s-a-b)]
Hvor s er semiperimeter:
s = (a + b + c + d) / 2.
I vores tilfælde er semiperimeteret s = 10 cm værd. Efter udskiftning af de respektive værdier:
a = 7 cm; b = 6 cm; c = 3 cm; d = 4 cm
Rester:
A = [10/4] √ [(3) (7) (- 1) (- 3)] = (5/2) √63 = 19,84 cm².
Højde
Højden h er relateret til området A ved følgende udtryk:
A = (a + c) ∙ h / 2, hvorfra højden kan opnås ved at rydde:
h = 2A / (a + c) = 2 * 19,84 / 10 = 3,988 cm.
Radius af den indskrevne cirkel
Radien af den indskrevne cirkel er lig med halvdelen af højden:
r = h / 2 = 1.984 cm
Diagonaler
Endelig findes diagonalernes længde:
d1 = √ [bto + a ∙ c - a (bto - dto) / (a - c)]
dto = √ [dto + a ∙ c - a (dto - bto) / (a - c)]
Korrekt erstatning af værdierne har vi:
d1 = √ [6to + 7 ∙ 3 - 7 (6to - 4to) / (7 - 3)] = √ (36 + 21-7 (20) / 4) = √ (22)
dto = √ [4to + 7 ∙ 3 - 7 (4to - 6to) / (7 - 3)] = √ (16 + 21-7 (-20) / 4) = √ (72)
Det vil sige: d1 = 4,69 cm og dto = 8,49 cm
Træning løst
Bestem trapezens indvendige vinkler med baser AB = a = 7, CD = c = 3 og laterale vinkler BC = b = 6, DA = d = 4.
Opløsning
Kosinosætningen kan anvendes til at bestemme vinklerne. For eksempel bestemmes vinklen ∠A = α ud fra trekanten ABD med AB = a = 7, BD = d2 = 8,49 og DA = d = 4.
Kosinosætningen anvendt på denne trekant ser sådan ud:
dtoto = ato + dto - 2 ∙ a ∙ d ∙ Cos (α), det vil sige:
72 = 49 + 16-56 ∙ Cos (α).
Løsning for opnås cosinus for vinkel α:
Cos (a) = -1/8
Det vil sige α = ArcCos (-1/8) = 97,18⁰.
På samme måde opnås de andre vinkler, hvis værdier er:
p = 41,41⁰; γ = 138,59⁰ og til sidst δ = 82,82⁰.
Referencer
- C. E. A. (2003). Geometrielementer: med kompasets øvelser og geometri. University of Medellin.
- Campos, F., Cerecedo, F. J. (2014). Matematik 2. Grupo Editorial Patria.
- Freed, K. (2007). Opdag polygoner. Benchmark Education Company.
- Hendrik, V. (2013). Generelle polygoner. Birkhäuser.
- IGER. (s.f.). Matematik Første semester Tacaná. IGER.
- Jr. geometri. (2014). Polygoner. Lulu Press, Inc..
- Miller, Heeren & Hornsby. (2006). Mathematics: Reasoning And Applications (Tiende udgave). Pearson Uddannelse.
- Patiño, M. (2006). Matematik 5. Redaktionel Progreso.
- Wikipedia. Trapes. Gendannet fra: es.wikipedia.com


Endnu ingen kommentarer