
Isosceles trapezoid egenskaber, sammenhænge og formler, eksempler
EN trapes ligebenede er en firkant, hvor to af siderne er parallelle med hinanden, og de to vinkler, der støder op til en af disse parallelle sider, har samme mål.
I figur 1 har vi den firsidede ABCD, hvor siderne AD og BC er parallelle. Derudover har vinklerne ∠DAB og ∠ADC ved siden af den parallelle side AD samme mål α.
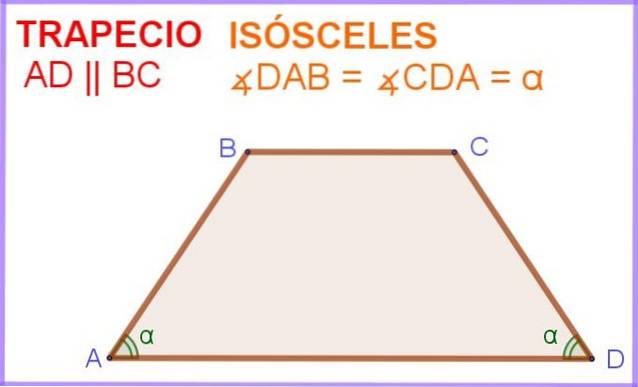
Så denne firkantede eller firesidede polygon er faktisk en ligebenet trapezformet.
I en trapesform kaldes de parallelle sider baser og de ikke-paralleller kaldes tværgående. En anden vigtig funktion er højde, som er den afstand, der adskiller de parallelle sider.
Ud over den ligebenede trapezoid er der andre typer trapezformede:
-Tskalen havtaske, som har alle dens forskellige vinkler og sider.
-Trektangel havfisk, hvor en lateral har lige tilstødende vinkler.
Den trapezformede form er almindelig inden for forskellige områder inden for design, arkitektur, elektronik, beregning og mange flere, som det vil fremgå senere. Derfor er det vigtigt at blive fortrolig med dens egenskaber.
Artikelindeks
- 1 egenskaber
- 1.1 Eksklusiver af den ligebenede trapez
- 1.2 For alle trapezider
- 2 Forhold og formler
- 2.1 Unikke forhold mellem den ligebenede trapezium
- 2.2 Forhold for enhver trapez
- 2.3 Forhold for ligebenet trapezoid med indskrevet omkreds
- 2.4 Formler til bestemmelse af den ene side, kendskab til de andre og en vinkel
- 2.5 Bestemmelse af den ene side, kendskab til de andre og en diagonal
- 2.6 Base fra højde, areal og anden base
- 2.7 Kendte laterale baser, areal og en vinkel
- 2.8 Kendt lateral median, areal og vinkel
- 2.9 Kendt højde på siderne
- 2.10 Kendt højde en vinkel og to sider
- 2.11 Kendte diagonaler på alle sider eller to sider og en vinkel
- 2.12 Omkrækningen af den ligebenede trekant
- 2.13 Areal af ligebenet trapez
- 2.14 Radius af den omskrevne cirkel
- 3 Eksempler på anvendelse af den ligebenede trapez
- 3.1 I arkitektur og konstruktion
- 3.2 I design
- 4 Løst øvelser
- 4.1 - Øvelse 1
- 4.2 - Øvelse 2
- 5 Referencer
Ejendomme
Eksklusiv til den ligebenede trapez
Hvis en trapez er ligebenet, har den følgende karakteristiske egenskaber:
1. - Siderne har samme måling.
2. - Vinklerne ved siden af baserne er ens.
3.- Modsatte vinkler er supplerende.
4.- Diagonalerne har samme længde, de to segmenter, der forbinder de modsatte hjørner, er de samme.
5.- Vinklen dannet mellem baserne og diagonalerne er alle af samme mål.
6.- Den har en begrænset omkreds.
Omvendt, hvis en trapezoid opfylder nogen af ovennævnte egenskaber, så er den en ligebenet trapezoid.
Hvis en af vinklerne er lige (90º) i en ligeben trapezform, vil alle de andre vinkler også være rigtige og danne et rektangel. Det vil sige, et rektangel er et særligt tilfælde af ligebenet trapez.

For al trapeze
Følgende sæt egenskaber er gyldigt for enhver trapez:
7.- Den median af trapezium, det vil sige segmentet, der forbinder midtpunkterne på dets ikke-parallelle sider, er parallelt med nogen af baserne.
8.- Medianlængden er lig med halvsummen (summen divideret med 2) af dens baser.
9.- En trapezs median skærer sine diagonaler ved midtpunktet.
10.- Trapezens diagonaler krydser hinanden på et punkt, der deler dem i to sektioner, der er proportionale med kvoterne i baserne.
11. - Summen af kvadraterne af diagonalerne på en trapez er lig med summen af kvadraterne på siderne plus det dobbelte produkt af baserne.
12.- Segmentet, der forbinder diagonalernes midtpunkter, har en længde svarende til halvforskellen mellem baserne.
13. - Vinklerne ved siden af de laterale er supplerende.
14. - En trapez har en indskrevet omkreds, hvis og kun hvis summen af dens baser er lig med summen af dens sider.
15. - Hvis en trapez har en indskrevet omkreds, så er vinklerne med et toppunkt i midten af omkredsen og sider, der passerer gennem enderne af samme side, retvinklede.
Forhold og formler
Følgende sæt af relationer og formler henviser til figur 3, hvor der foruden ligebenet trapezoid er vist andre vigtige segmenter, der allerede er nævnt, såsom diagonaler, højde og median.
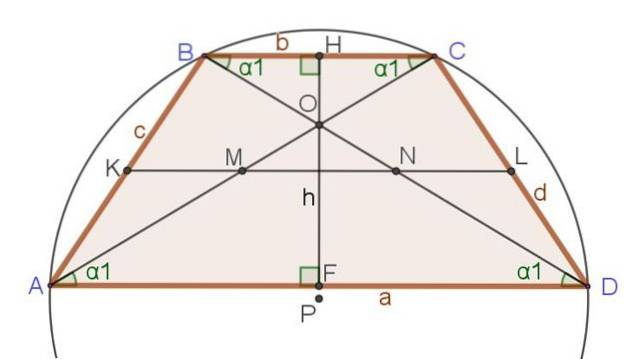
Unikke forhold mellem den ligebenede trapezium
1.- AB = DC = c = d
2.- ∡DAB = ∡CDA og ∡ABC = ∡BCD
3.- ∡DAB + ∡BCD = 180º og ∡CDA + ∡ABC = 180º
4.- BD = AC
5.- ∡CAD = ∡BDA = ∡CBD = ∡BCA = α1
6.- A, B, C og D hører til den afgrænsede cirkel.
Forhold til enhver trapez
- Hvis AK = KB og DL = LC ⇒ KL || AD og KL || F.Kr.
8.- KL = (AD + BC) / 2
9.- AM = MC = AC / 2 og DN = NB = DB / 2
10.- AO / OC = AD / BC og DO / OB = AD / BC
11. - ACto + DBto = ABto + DCto + 2⋅AD⋅BC
12.- MN = (AD - BC) / 2
13.- ∡DAB + ∡ABC = 180º og ∡CDA + ∡BCD = 180º
14.- Hvis AD + BC = AB + DC ⇒ ∃ R end lige langt fra AD, BC, AB og DC
15.- Hvis ∃ R er lige langt fra AD, BC, AB og DC, så:
∡BRA = ∡DRC = 90º
Forhold for ligebenet trapezformet med indskrevet omkreds
Hvis summen af baserne i en ensartet trapez er lig med to gange en lateral, så eksisterer den indskrevne omkreds.

Følgende egenskaber gælder, når den ligebenede trapez har en indskrevet omkreds (se figur 4 ovenfor):
16.- KL = AB = DC = (AD + BC) / 2
17. - Diagonalerne krydser hinanden vinkelret: AC ⊥ BD
18.- Højden måler det samme som medianen: HF = KL, det vil sige h = m.
19.- Kvadratet af højden er lig med basenes produkt: hto = BC⋅AD
20.- Under disse specifikke forhold er trapezens areal lig med kvadratet i højden eller produktet af baserne: Areal = hto = BC⋅AD.
Formler til bestemmelse af den ene side, kendskab til de andre og en vinkel
Kendt en base, den laterale og en vinkel, den anden base kan bestemmes af:
a = b + 2c Cos α
b = a - 2c Cos α
Hvis længden af baserne og en vinkel er givet som kendte data, er længderne på begge sider:
c = (a - b) / (2 Cos a)
Bestemmelse af den ene side, kendskab til de andre og en diagonal
a = (d1to - cto) / b;
b = (d1to - cto)/ til
c = √ (d1to - a⋅b)
Hvor d1 er diagonalernes længde.
Base fra højde, areal og anden base
a = (2 A) / h - b
b = (2 A) / h - a
Kendte laterale baser, areal og en vinkel
c = (2A) / [(a + b) sin α]
Kendt lateral median, areal og vinkel
c = A / (m sin α)
Kendt højde på siderne
h = √ [4 cto - (a - b)to]
Kendt højde en vinkel og to sider
h = tg α⋅ (a - b) / 2 = c. sin α
Kendte diagonaler på alle sider eller to sider og en vinkel
d1 = √ (cto+ a b)
d1 = √ (ato+ cto - 2 a c Cos α)
d1 = √ (bto + cto- 2 b c Cos β)
Omkanten af den ligebenede trekant
P = a + b + 2c
Isosceles trapezium-område
Der er flere formler til beregning af området afhængigt af de kendte data. Følgende er det mest kendte, afhængigt af baser og højde:
A = h⋅ (a + b) / 2
Og du kan også bruge disse andre:
-Hvis siderne er kendte
A = [(a + b) / 4] √ [4cto - (a - b)to]
-Når du har to sider og en vinkel
A = (b + c Cos α) c Sen α = (a - c Cos α) c Sen α
-Hvis radius af den indskrevne cirkel og en vinkel er kendt
A = 4 rto / Sen α = 4 rto / Sen β
-Når baserne og en vinkel er kendt
A = a⋅b / Sen α = a⋅b / Sen β
-Hvis trapesformet kan være indskrevet en omkreds
A = c⋅√ (a⋅b) = m⋅√ (a⋅b) = r⋅ (a + b) / 2
-Kendte diagonalerne og den vinkel, de danner med hinanden
A = (d1to/ 2) Sen y = (d1to / 2) Sen δ
-Når du har lateral, median og en vinkel
A = mc.sen α = mc.sen β
Radius af den omskrevne cirkel
Kun ligebenede trapezoider har en begrænset omkreds. Hvis den større base a er den laterale c og den diagonale d kendt1, derefter er radius R for cirklen, der passerer gennem trapezens fire hjørner:
R = a⋅c⋅d1 / 4√ [p (p -a) (p -c) (p-d1)]
Hvor p = (a + c + d1) / to
Eksempler på brug af den ligebenede trapez
Den ligebenede trapezform vises i designfeltet, som det ses i figur 2. Og her er nogle yderligere eksempler:
Inden for arkitektur og konstruktion
De gamle inkaer kendte den ligebenede trapezform og brugte den som et bygningselement i dette vindue i Cuzco, Peru:

Og her vises trapesen igen i opkaldet trapesformet ark, et materiale, der ofte bruges i konstruktionen:

I design
Vi har allerede set, at den ligebenede trapezform forekommer i hverdagsgenstande, herunder mad som denne chokoladestang:

Løst øvelser
- Øvelse 1
En ligebenet trapez har en base større end 9 cm, en base mindre end 3 cm og dens diagonaler 8 cm hver. Beregn:
a) Side
b) Højde
c) Omkreds
d) Område
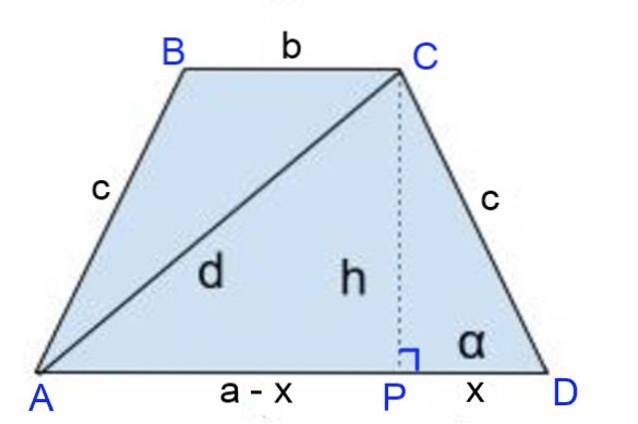
Løsning til
Højden CP = h er afbildet, hvor højdefoden definerer segmenterne:
PD = x = (a-b) / 2 y
AP = a - x = a - a / 2 + b / 2 = (a + b) / 2.
Brug af Pythagoras sætning til højre trekant DPC:
cto = hto + (a - b)to / 4
Og også til højre trekant APC:
dto = hto + APto = hto + (a + b)to / 4
Endelig, medlem for medlem, trækkes den anden ligning fra den første og forenkles:
dto - cto = ¼ [(a + b)to - (a-b)to] = ¼ [(a + b + a-b) (a + b-a + b)]
dto - cto = ¼ [2a 2b] = a b
cto= dto - a b ⇒ c = √ (dto - a b) = √ (8to - 9⋅3) = √37 = 6,08 cm
Løsning b
hto = dto - (a + b)to / 4 = 8to - (12to / toto ) = 8to - 6to = 28
h = 2 √7 = 5,29 cm
Løsning c
Omkreds = a + b + 2 c = 9 + 3 + 2⋅6,083 = 24,166 cm
Løsning d
Areal = h (a + b) / 2 = 5,29 (12) / 2 = 31,74 cm
- Øvelse 2
Der er en ligebenet trapezform, hvis største base er dobbelt den mindste og dens mindste base er lig med højden, som er 6 cm. Beslutte:
a) Længden af den laterale
b) Omkreds
c) Område
d) Vinkler
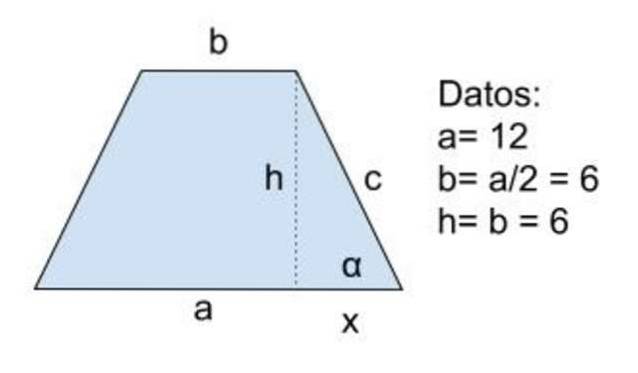
Løsning til
Data: a = 12, b = a / 2 = 6 og h = b = 6
Vi fortsætter på denne måde: højden h tegnes, og den Pythagoras sætning påføres hypotenus trekanten "c" og benene h og x:
cto = hto+xcto
Derefter skal du beregne værdien af højden ud fra dataene (h = b) og den for benet x:
a = b + 2 x ⇒ x = (a-b) / 2
Udskiftning af de tidligere udtryk, vi har:
cto = bto+(a-b)to/toto
Nu introduceres de numeriske værdier, og det forenkles:
cto = 62+ (12-6) 2/4
cto = 62 (1 + ¼) = 62 (5/4)
Opnåelse:
c = 3√5 = 6,71 cm
Løsning b
Omkredsen P = a + b + 2 c
P = 12 + 6 + 6√5 = 6 (8 + √5) = 61,42 cm
Løsning c
Området som funktion af basernes højde og længde er:
A = h⋅ (a + b) / 2 = 6⋅ (12 + 6) / 2 = 54 cmto
Løsning d
Vinklen α dannet af lateral med den større base opnås ved trigonometri:
Tan (α) = h / x = 6/3 = 2
α = ArcTan (2) = 63,44º
Den anden vinkel, den der danner lateral med den mindre base, er β, som er supplerende med α:
β = 180º - α = 180º - 63.44º = 116.56º
Referencer
- E. A. 2003. Elementer af geometri: med øvelser og kompasgeometri. University of Medellin.
- Campos, F. 2014. Matematik 2. Grupo Editorial Patria.
- Freed, K. 2007. Opdag polygoner. Benchmark Education Company.
- Hendrik, V. 2013. Generaliserede polygoner. Birkhäuser.
- IGER. Matematik Første semester Tacaná. IGER.
- Jr. geometri. 2014. Polygoner. Lulu Press, Inc..
- Miller, Heeren & Hornsby. 2006. Matematik: ræsonnement og applikationer. 10. Udgave. Pearson Uddannelse.
- Patiño, M. 2006. Matematik 5. Redaktionel progreso.
- Wikipedia. Trapes. Gendannet fra: es.wikipedia.com



Endnu ingen kommentarer