
Balancering af vektorberegning, eksempler, øvelser
Det balancerende vektor Det er den, der er modsat den resulterende vektor og derfor er i stand til at afbalancere et system, da det har samme størrelse og samme retning, men den modsatte retning af dette.
Ved mange lejligheder henviser balanceringsvektoren til en kraftvektor. For at beregne afbalanceringskraften skal du først finde den resulterende kraft som vist i følgende figur:
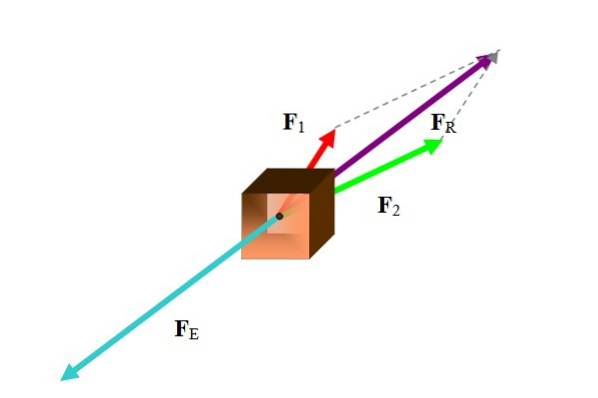
Der er forskellige metoder til at udføre denne opgave afhængigt af de foreliggende data. Da kræfterne er vektorer, er den resulterende vektorsummen af de deltagende kræfter:
FR = F1 + Fto + F3 + ... .
Blandt de anvendte metoder er grafiske metoder såsom polygonal, parallelogram og analytiske metoder såsom nedbrydning af kræfter i deres kartesiske komponenter. I eksemplet anvendte figuren parallelogrammetoden.
Når først den resulterende kraft er fundet, er afbalanceringskraften lige den modsatte vektor.
Ja FOG er afbalanceringskraften, så er det tilfreds med det FOG anvendt på et bestemt tidspunkt, garanterer det systemets translationelle ligevægt. Hvis det er en enkelt partikel, bevæger den sig ikke (eller måske med konstant hastighed), men hvis det er et udvidet objekt, har det stadig evnen til at rotere:
FR + FOG = 0
Artikelindeks
- 1 Eksempler
- 1.1 Tvinge bord
- 2 Løst øvelser
- 2.1-Øvelse 1
- 2.2-Øvelse 2
- 3 Referencer
Eksempler
Balanceringskræfter er til stede overalt. Vi er selv afbalanceret af den kraft, som stolen udøver for at kompensere for vægten. Genstandene, der er i ro: bøger, møbler, loftslamper og et stort antal mekanismer, balanceres løbende af kræfter.
For eksempel er en bog i ro på et bord afbalanceret af den normale kraft, som den udøver på bogen, hvilket forhindrer den i at falde. Det samme sker med kæden eller kablet, der holder lampen hængende fra loftet i et rum. Kablerne, der holder en belastning, fordeler deres vægt gennem spændingen i dem.
I en væske er nogle genstande i stand til at flyde og forblive i ro, da deres vægt er afbalanceret af en opadgående kraft, der udøves af væsken, kaldet skubbe.
Forskellige mekanismer skal afbalanceres, idet man kender balanceringskraftvektoren som stænger, bjælker og søjler.
Når du bruger en skala, er det nødvendigt på en eller anden måde at afbalancere genstandens vægt med en styrke, der er ækvivalent, enten ved at tilføje vægte eller ved hjælp af fjedre..
Tving bord
Krafttabellen bruges i laboratoriet til at bestemme afbalanceringskraften. Den består af en cirkulær platform, hvorfra du har set ovenfra i figuren, og som har en vinkelmåler til måling af vinkler.
På kanterne af bordet er der remskiver, gennem hvilke reb, der holder vægte, og som konvergerer i en ring, der er i midten.
For eksempel hænges to vægte. Spændingerne, der genereres i strengene af disse vægte, er tegnet med rødt og blåt i figur 2. En tredje vægt i grønt kan afbalancere den resulterende kraft af de to andre og holde systemet i balance..
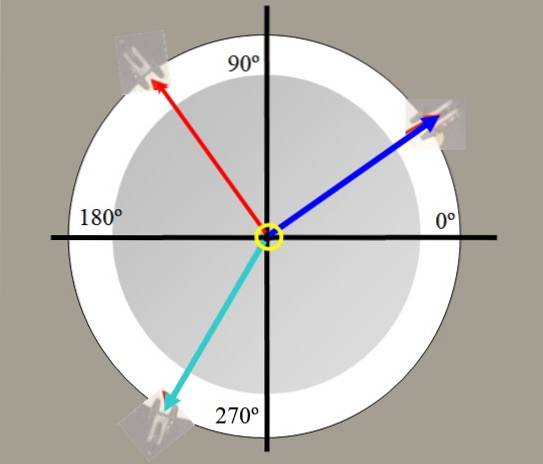
Med styrketabellen er det muligt at verificere kræftens vektorkarakter, nedbryde kræfter, finde afbalanceringskraften og verificere Lamys sætning:
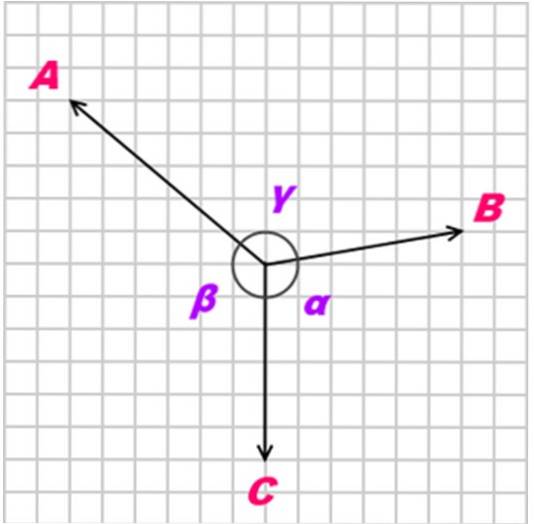
Hvis en krop er i ligevægt takket være tre coplanare kræfter, samtidige og ikke-kollinære (ikke parallelle), kaldet TIL, B Y C, forholdet mellem disse kræfter er som følger:
A / sin α = B / sin β = C / sin γ
Løst øvelser
-Øvelse 1
225 g (blå spænding) og 150 g (rød spænding) vægt hænges på kraftbordet i figur 2 med de viste vinkler. Find værdien af afbalanceringskraften og den vinkel, den udgør med den lodrette akse.
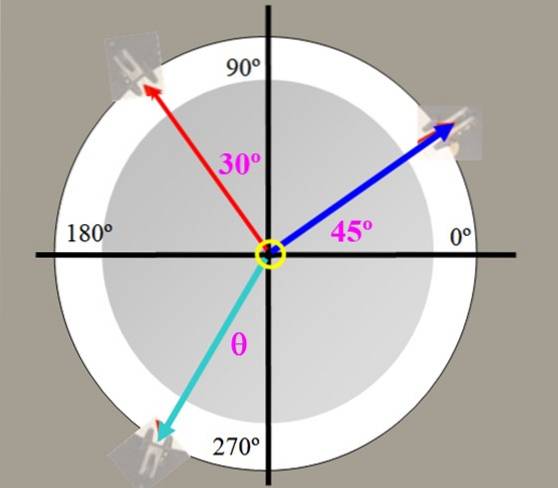
Opløsning
Problemet kan arbejdes med vægtene udtrykt i gram (kræfter). Lad P1 = 150 gram og Pto = 225 gram, de respektive komponenter i hver er:
P1x = 225. cos 45 ° g = 159,10 g; P1 år = 225. cos 45º g = 159,10 g
P2x = -150. sin 30 g = -75,00 g; P2 og = 150. cos 30º g = 129,90 g
Den resulterende vægt PR findes ved algebraisk at tilføje komponenterne:
PRx = 159,10 - 75,00 g = 84,10 g
PRy = 159,10 + 129,90 g = 289,00 g
Balanceringsvægten POG er vektoren modsat PR:
PTidligere = -84,10 g
PHej = -289,00 g
Balanceringsvægtens størrelse beregnes ved:
POG = (STidligereto + PHejto)1/2 = ((-84,10)to + (-289,00)to)1/2 g = 301 g
Vinklen θ i figuren er:
θ = arctg (-84.10 / -289.00) = 16.2º i forhold til aksen Y negativ.
-Øvelse 2
Find balanceringsvektoren for systemet vist i figuren, idet du ved, at hver firkant måler 10 m på en side.
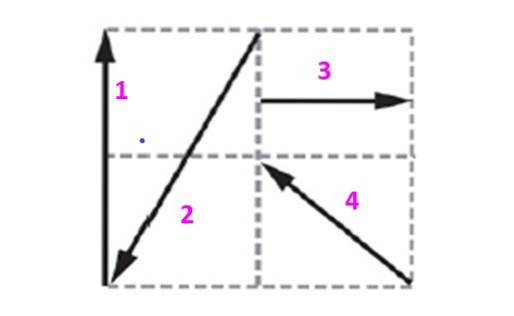
Opløsning
Vektorerne indeholdt i dette gitter udtrykkes i form af enheds- og ortogonale vektorer jeg Y j der bestemmer flyet. Vektor 1, der betegnes som v1 den har en størrelse på 20 m og er rettet lodret opad. Det kan udtrykkes som:
v1 = 0 jeg +tyve j m
Fra tegningen kan det ses, at vektor 2 er:
vto = -10 jeg - tyve j m
Vektor 3 er vandret og peger i den positive retning:
v3 = 10 jeg + 0 j m
Endelig hældes vektor 4 45 °, da den er diagonalen på firkanten, og derfor måler dens komponenter det samme:
v4 = -10 jeg + 10 j m
Bemærk, at skiltene angiver, hvilken side af aksen komponenterne er: over og til højre har et + tegn, mens de under og til venstre har et tegn -.
Den resulterende vektor opnås ved at tilføje komponent til komponent:
vR = -10 jeg + 10 j m
Derefter er systemets afbalanceringsvektor:
vOG = 10 jeg - 10 j m
Referencer
- Beardon, T. 2011. En introduktion til vektorer. Hentet fra: nrich.maths.org.
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley. 38-52.
- Figueroa, D. Series: Physics for Sciences and Engineering. Bind 1. kinematik. 31-68.
- Fysisk. Modul 8: Vektorer. Gendannet fra: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mekanik for ingeniører. Statisk. 6. udgave. Continental Publishing Company. 15-53.
- Vector Addition Lommeregner. Gendannet fra: 1728.org
- Vektorer. Gendannet fra: wikibooks.org

Endnu ingen kommentarer