
Vektorer i rummet hvordan man tegner graf, applikationer, øvelser
EN vektor i rummet er alle repræsenteret af et koordinatsystem givet af x, Y Y z. Næsten altid flyet xy er planet for den vandrette overflade og aksen z repræsenterer højde (eller dybde).
De kartesiske koordinatakser vist i figur 1 opdeler mellemrum i 8 kaldte regioner oktanter, analogt med hvordan akser x - Y del flyet i 4 kvadranter. Vi får så 1. oktant, 2. oktant og så videre.
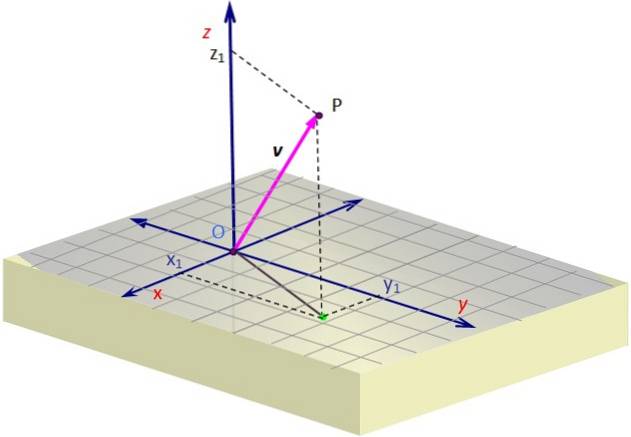
Figur 1 viser en repræsentation af en vektor v i rummet. Der kræves noget perspektiv for at skabe illusionen af tre dimensioner på skærmens plan, hvilket opnås ved at tegne et skråt billede.
For at tegne en 3D-vektor skal du bruge de stiplede linjer, der på gitteret bestemmer koordinaterne for projektionen eller "skyggen" af v Over overfladen x-y. Denne projektion begynder ved O og slutter ved det grønne punkt.
Når du er der, skal du fortsætte langs lodret til den nødvendige højde (eller dybde) i henhold til værdien af z, indtil den når P. Vektoren tegnes startende fra O og slutter ved P, som i eksemplet er i 1. oktant.
Artikelindeks
- 1 Ansøgninger
- 2 Notation og repræsentationer af vektorer i 3D
- 2.1 Vinkler og regissorkosinus af en vektor
- 3 Løst øvelser
- 3.1-Øvelse 1
- 3.2-Øvelse 2
- 4 Referencer
Ansøgninger
Vektorer i rummet bruges i vid udstrækning i mekanik og andre grene inden for fysik og teknik, da strukturer, der omgiver os, kræver geometri i tre dimensioner..
Positionsvektorer i rummet bruges til at placere objekter i forhold til et kaldet referencepunkt kilde O. Derfor er de også nødvendige redskaber til navigation, men det er ikke alt.
Styrker, der virker på strukturer som bolte, beslag, kabler, stivere og mere, er vektor af natur og orienteret i rummet. For at kende dens virkning er det nødvendigt at kende dens adresse (og også dens anvendelsessted).
Og ofte kendes styrkens retning ved at kende to punkter i rummet, der hører til dens handlingslinje. På denne måde er kraften:
F = F eller
Hvor F er styrke eller modul af kraften og eller er enhedsvektoren (af modul 1) rettet langs handlingslinjen for F.
Notation og 3D-vektorrepræsentationer
Før vi fortsætter med at løse nogle eksempler, gennemgår vi kort 3D-vektornotation.
I eksemplet i figur 1 har vektoren v, hvis oprindelsespunkt falder sammen med oprindelsen O, og hvis ende er punkt P, koordinater x Y z positiv, mens koordinaten Y er negativ. Disse koordinater er: x1, Y1, z1, som er nøjagtigt koordinaterne for P.
Så hvis vi har en vektor knyttet til oprindelsen, det vil sige hvis startpunkt falder sammen med O, er det meget let at indikere dens koordinater, som vil være dem til det ekstreme punkt eller P. For at skelne mellem et punkt og en vektor, vi bruger til de sidste fede bogstaver og parenteser som denne:
v = < x1, Y1, z1 >
Mens punkt P er angivet med parenteser:
P = (x1, Y1, z1)
En anden repræsentation gør brug af enhedsvektorer jeg, j Y k der definerer de tre rumretninger på akserne x, Y Y z henholdsvis.
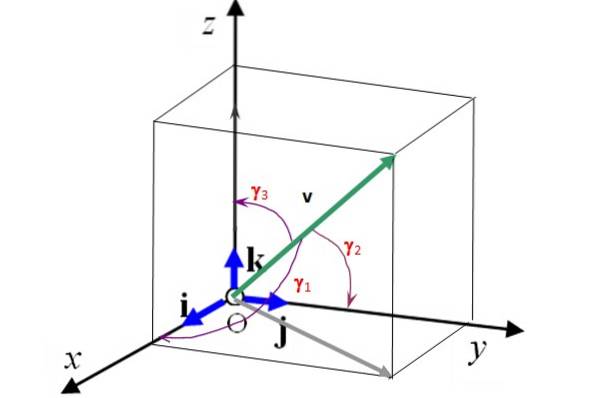
Disse vektorer er vinkelrette på hinanden og danner en ortonormal base (se figur 2). Dette betyder, at en 3D-vektor kan skrives i form af dem som:
v = vx jeg + vY j + vz k
Vinkler og retning af cosinus af en vektor
Figur 2 viser også direktørvinklerne γ1, γto og γ3 end vektor v gør henholdsvis med akserne x, Y Y z. At kende disse vinkler og størrelsen af vektoren er det helt bestemt. Derudover møder regissørens vinkler følgende forhold:
(cos γ1)to + (cos γto)to + (cos γ3)to = 1
Løst øvelser
-Øvelse 1
I figur 2 er vinklerne γ1, γto og γ3 end vektor v af modul 50 form med koordinatakserne er henholdsvis: 75,0º, 60,0º og 34,3º. Find de kartesiske komponenter i denne vektor og repræsenter den i form af enhedsvektorerne jeg, j Y k.
Opløsning
Vektor projektion v på aksen x er Vx = 50. cos 75º = 12.941. Tilsvarende fremskrivning af v på aksen Y er VY = 50 cos 60 º = 25 og endelig på aksen z er Vz = 50. cos 34,3º = 41,3. Nu v kan udtrykkes som:
v = 12,9 jeg + 25,0 j + 41.3 k
-Øvelse 2
Find spændingerne i hvert af kablerne, der holder skovlen i figuren i ligevægt, hvis dens vægt er 30 N.
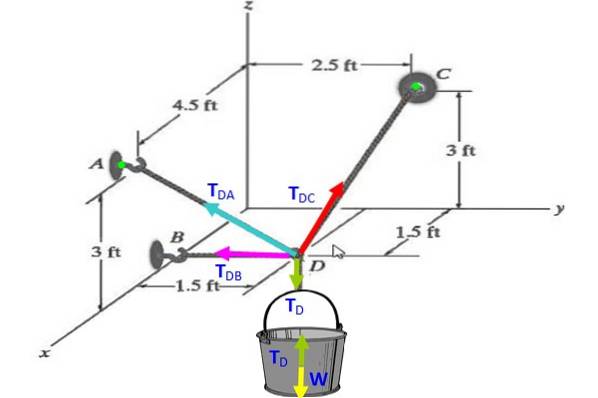
Opløsning
På skovlen viser diagrammet til fri krop det TD (grøn) udligner vægten W (gul), derfor TD = W = 30 N..
I knuden, vektoren TD er lodret lodret nedad, så:
TD = 30 (-k) N.
Følg disse trin for at etablere de resterende spændinger:
Trin 1: Find koordinaterne for alle punkter
A = (4,5,0,3) (A er på væggens plan x-z)
B = (1,5,0,0) (B er på x-aksen)
C = (0, 2,5, 3) (C er på vægens plan og Z)
D = (1,5, 1,5, 0) (D er i vandret plan x-y)
Trin 2: Find vektorerne i hver retning ved at trække koordinaterne for slutningen og begyndelsen
GIVER = <3; -1.5; 3>
DC = <-1.5; 1; 3>
DB = <0; -1.5 ; 0>
Trin 3: Beregn moduler og enhedsvektorer
En enhedsvektor opnås ved udtrykket: eller = r / r, med r (med fed skrift) som vektor og r (ikke med fed skrift) som modul for vektor.
DA = (3to + (-1,5)to + 3to)½ = 4,5; DC = ((-1,5) to + 1to + 3to)½ = 3,5
ellerGIVER = <3; -1.5; 3>4,5 = <0.67 ; -0.33 ; 0.67>
ellerDC = <-1.5; 1; 3>3,5 = <-0.43; 0.29; 0.86>
ellerDB = <0; -1; 0>
ellerD = <0; 0; -1>
Trin 4: Udtryk alle spændinger som vektorer
TGIVER = TGIVER ellerGIVER = TGIVER<0.67 ; -0.33 ; 0.67>
TDC = TDC ellerDC = TDC <-0.43; 0.29; 0.86>
TDB = TDB ellerDB = TDB <0; -1; 0>
TD = 30 <0; 0; -1>
Trin 5: Anvend den statiske ligevægtstilstand og løs ligningssystemet
Endelig anvendes tilstanden for statisk ligevægt på skovlen, så vektorsummen af alle kræfterne på noden er nul:
TGIVER + TDC + TDB + TD = 0
Da spændingerne er i rummet, vil det resultere i et system med tre ligninger for hver komponent (x, og og z) af spændingerne.
0,67 TGIVER -0,43 TDC + 0 TDB = 0
-0,33 TGIVER + 0,29 TDC - TDB = 0
0,67 TGIVER + 0,86 TDC +0 TDB - 30 = 0
Løsningen er: TGIVER = 14,9 N; TGIVER = 23,3 N; TDB = 1,82 N
Referencer
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley. 38-52.
- Figueroa, D. Series: Physics for Sciences and Engineering. Bind 1. kinematik. 31-68.
- Fysisk. Modul 8: Vektorer. Gendannet fra: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mekanik for ingeniører. Statisk. 6. udgave. Continental Publishing Company. 15-53.
- Vector Addition Lommeregner. Gendannet fra: 1728.org



Endnu ingen kommentarer