
Gennemsnitlig vinkelhastighedsdefinition og formler, løste øvelser
Det gennemsnitlig vinkelhastighed Rotation er defineret som den vinkel, der roteres pr. Tidsenhed for positionsvektoren for et punkt, der beskriver cirkelbevægelse. Bladene til en loftsventilator (som den, der er vist i figur 1), følger cirkulær bevægelse, og deres gennemsnitlige vinkel på omdrejningshastighed beregnes ved at tage kvotienten mellem den drejede vinkel og det tidspunkt, hvor vinklen blev bevæget..
Reglerne, som rotationsbevægelse følger, svarer noget til de velkendte regler for translationel bevægelse. De tilbagelagte afstande kan også måles i meter, men vinkelstørrelserne får særlig relevans, fordi de i høj grad letter beskrivelsen af bevægelsen.
Generelt anvendes græske bogstaver til de vinkelmængder og latinske bogstaver til de tilsvarende lineære størrelser..
Artikelindeks
- 1 Definition og formler
- 1.1 Ensartet rotation
- 2 Løst øvelser
- 2.1-Øvelse 1
- 2.2-Øvelse 2
- 3 Referencer
Definition og formler
Figur 2 repræsenterer bevægelsen af et punkt på en cirkulær sti c. Punktets position P svarer til øjeblikket t, og vinkelpositionen svarende til det øjeblik er ϕ.
Fra øjeblikket t forløber en periode Δt. I denne periode er punktets nye position P ', og vinkelpositionen er steget med en vinkel Δϕ.
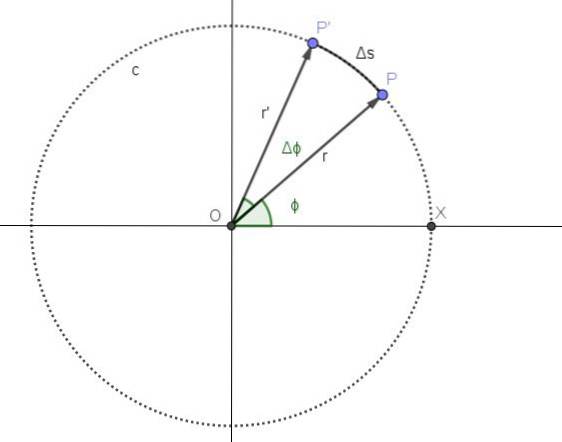
Den gennemsnitlige vinkelhastighed ω er den vinklede bevægelse pr. Tidsenhed, så kvotienten Δ / Δt repræsenterer den gennemsnitlige vinkelhastighed mellem gange t og t + Δt:
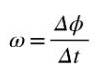
Da vinklen måles i radianer og tiden i sekunder, er enheden for den gennemsnitlige vinkelhastighed rad / s. Hvis du vil beregne Vinkelhastighed lige i øjeblikket t, så bliver vi nødt til at beregne kvotienten Δϕ / Δt når Δt ➡0.

Ensartet rotation
En rotationsbevægelse er ensartet, hvis den bevægede vinkel på et hvilket som helst observeret øjeblik er den samme i samme tidsperiode. Hvis rotationen er ensartet, falder vinkelhastigheden på ethvert tidspunkt sammen med den gennemsnitlige vinkelhastighed.
I en ensartet rotationsbevægelse kaldes den tid, hvor en fuldstændig revolution foretages periode og er betegnet med T.
Når en komplet drejning er foretaget, er den vandrede vinkel endvidere 2π, så i en ensartet rotation er vinkelhastigheden related relateret til perioden T ved hjælp af følgende formel:
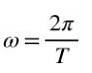
Det definerer frekvens F af en ensartet rotation som kvotienten mellem antallet af drejninger og den tid, der bruges til at gå igennem dem, det vil sige, hvis N drejninger foretages i tidsperioden At, så vil frekvensen være:
f = N / At
Da en tur (N = 1) køres i tid T (perioden), opnås følgende forhold:
f = 1 / T
Det vil sige, i en ensartet rotation er vinkelhastigheden relateret til frekvensen gennem forholdet:
ω = 2π ・ f
Forholdet mellem vinkelhastighed og lineær hastighed
Lineær hastighed v, er kvotienten mellem den tilbagelagte afstand og den tid, det tager at rejse den. I figur 2 er den tilbagelagte afstand buelængden Δs.
Buen Δs er proportional med den vandrede vinkel Δϕ og radius r, hvor følgende forhold er opfyldt:
Δs = r ・ Δϕ
Så længe Δϕ måles i radianer.
Hvis vi deler det forrige udtryk med tidsforløbet Δt, får vi:
(Δs / Δt) = r ・ (Δϕ / Δt)
Kvotienten for det første element er den lineære hastighed, og kvoten for det andet medlem er den gennemsnitlige vinkelhastighed:
v = r ・ ω
Løst øvelser
-Øvelse 1
Spidserne på loftsventilatorens vinger vist i figur 1 bevæger sig med en hastighed på 5 m / s, og vingerne har en radius på 40 cm.
Beregn med disse data: i) hjulets gennemsnitlige vinkelhastighed, ii) antallet af drejninger, hjulet foretager på et sekund, iii) perioden i sekunder.
Opløsning
i) Den lineære hastighed er v = 5 m / s.
Radien er r = 0,40 m.
Fra forholdet mellem lineær hastighed og vinkelhastighed løser vi sidstnævnte:
v = r ・ ω => ω = v / r = (5 m / s) / (0,40 m) = 12,57 rad / s
ii) ω = 2π ・ f => f = ω / 2π = (12,57 rad / s) / (2π rad) = 2 omdrejninger / s
iii) T = 1 / f = 1 / (2 omdrejninger / s) = 0,5 s for hver tur.
-Øvelse 2
En legetøjsvogn bevæger sig på et cirkulært spor med en radius på 2 m. Ved 0s er dens vinkelposition 0 rad, men efter tid t er dens vinkelposition
φ (t) = 2 ・ t .
Med disse data
i) Beregn den gennemsnitlige vinkelhastighed i de følgende tidsintervaller [0s, 0,5s]; [0,5s, 1,0s]; [1.0s, 1.5s] og endelig i perioden [0.0s, 1.5s].
ii) Baseret på resultaterne af del i) Hvad kan man sige om bevægelsen?
iii) Bestem den gennemsnitlige lineære hastighed i samme tidsperiode fra del i)
iv) Find vinkelhastigheden og den lineære hastighed i ethvert øjeblik.
Opløsning
i) Den gennemsnitlige vinkelhastighed er givet ved følgende formel:
Vi fortsætter med at beregne den tilbagelagte vinkel og den forløbne tid i hvert interval.
Interval 1: Δϕ = ϕ (0,5s) - ϕ (0,0s) = 2 (rad / s) * 0,5s - 2 (rad / s) * 0,0s = 1,0 rad
Δt = 0,5s - 0,0s = 0,5s
ω = Δϕ / Δt = 1.0rad / 0.5s = 2.0 rad / s
Interval 2: Δϕ = ϕ (1.0s) - ϕ (0.5s) = 2 (rad / s) * 1.0s - 2 (rad / s) * 0.5s = 1.0 rad
Δt = 1,0s - 0,5s = 0,5s
ω = Δϕ / Δt = 1.0rad / 0.5s = 2.0 rad / s
Interval 3: Δϕ = ϕ (1.5s) - ϕ (1.0s) = 2 (rad / s) * 1.5s - 2 (rad / s) * 1.0s = 1.0 rad
Δt = 1,5s - 1,0s = 0,5s
ω = Δϕ / Δt = 1.0rad / 0.5s = 2.0 rad / s
Interval 4: Δϕ = ϕ (1,5s) - ϕ (0,0s) = 2 (rad / s) * 1,5s - 2 (rad / s) * 0,0s = 3,0 rad
Δt = 1,5s - 0,0s = 1,5s
ω = Δϕ / Δt = 3,0rad / 1,5s = 2,0 rad / s
ii) I betragtning af de tidligere resultater, hvor den gennemsnitlige vinkelhastighed blev beregnet i forskellige tidsintervaller, hvilket altid opnåede det samme resultat, ser det ud til at indikere, at det er en ensartet cirkulær bevægelse. Disse resultater er dog ikke afgørende..
Måden at sikre konklusionen på er at beregne den gennemsnitlige vinkelhastighed for et vilkårligt interval [t, t ']: Δϕ = ϕ (t') - ϕ (t) = 2 * t '- 2 * t = 2 * (t '-t)
Δt = t '- t
ω = Δϕ / Δt = 2 * (t'-t) / (t'-t) = 2,0 rad / s
Dette betyder, at legetøjsvognen har en konstant gennemsnitlig vinkelhastighed på 2 rad / s i løbet af den betragtede periode. Men du kan gå længere, hvis du beregner den øjeblikkelige vinkelhastighed:
Dette fortolkes som, at legetøjsbilen til enhver tid har konstant vinkelhastighed = 2 rad / s.
Referencer
- Giancoli, D. Fysik. Principper med applikationer. 6. udgave. Prentice Hall. 30-45.
- Kirkpatrick, L. 2007. Fysik: Et blik på verden. 6ta Forkortet udgave. Cengage læring. 117.
- Resnick, R. (1999). Fysisk. Bind 1. tredje udgave på spansk. Mexico. Compañía Editorial Continental S.A. de C.V. 33-52.
- Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 1. 7. Udgave. Mexico. Cengage Learning Editors. 32-55.
- Wikipedia. Vinkelhastighed. Gendannet fra: wikipedia.com

Endnu ingen kommentarer